В соответствующей окружности нарисуйте угол равный 2a

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Ваш ответ

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

решение вопроса

Видео:Построить угол , равный данному.Скачать

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,949
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN — ⋃MN = 180° — 70° = 110°

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Видео:Вписанный угол равен половине центрального углаСкачать

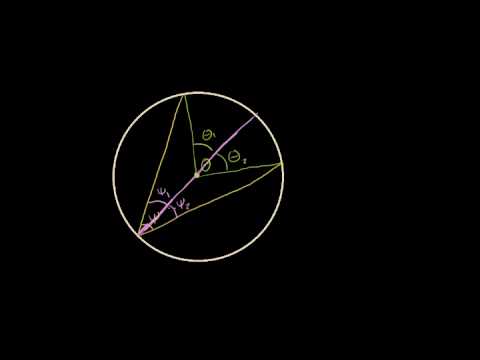
Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Видео:Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Задание. Чему равен ∠AВС на рисунке?

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

Видео:Вписанные углы в окружностиСкачать

Ответы на Конкурс «Смарт КЕНГУРУ» 25 января 2022 года

Всероссийский конкурс «Смарт КЕНГУРУ» пройдет 25 января 2022 года для учащихся 2-10 классов.

Формат конкурса следующий:

— 20 задач с выбором ответа (для 2 класса – 15);

— на решение отводится 50 минут;

— задачи трех категорий трудности: по 8 задач на 3 балла и на 4 балла, 4 задачи на 5 баллов (для 2 класса – 6, 6 и 3).

Все участники получают сертификат со своим результатом и памятный подарок.

Школы получают:

— дипломы и подарки лучшим участникам;

— сертификат победителям по параллели;

— отчет по параллелям;

— свидетельство школьному организатору;

— благодарственные письма для учителей, проводивших конкурс

Мероприятия проходят при поддержке таких авторитетных организаций, как:

— Санкт-Петербургское отделение математического института им. В. А. Стеклова РАН;

— Математический факультет Российского государственного педагогического университета им. А. И. Герцена;

Видео:Построение 8 угольника циркулемСкачать

Вопросы и ответы для 3-4 класса

1. Смартик выписал первые буквы названий всех цифр. Сколько из этих букв встречаются в слове СМАРТИК?

1. Смартик построил домики из деталей трех видов. В каком из домиков меньше деталей, чем в остальных?

1. Как называется одно из арифметических действий?

Ответ: Г — вычитание

4.Какое число получится, если выписать цифры, двигаясь по стрелочкам на рисунке?

1. Электронные часы сейчас показывают 10 :10. Через сколько минут на часах будет тот же набор цифр?

1. Прямоугольный коврик размером 2 × 3 сшит из шести квадратиков. Три таких коврика положили на пол, как показано на рисунке. В середину какого квадратика надо вбить гвоздик, чтобы приколотить к полу все три коврика?

1. В альбоме с раскрасками Маша раскрашивает каждый день по одной картинке. Первую картинку она раскрасила в пятницу. В какой день Маша раскрасит пятую картинку?

Ответ: Г — во вторник

1. У Насти на новогодней елке было 19 игрушек: шарики, звездочки и фонарики. Из них 10 игрушек — не шарики, а звездочек на 2 меньше, чем шариков. Сколько фонариков было на елке?

Задачи, оцениваемые в 4 балла

1. Из лагеря выехала группа велосипедистов, всего 16 человек. Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово?

Видео:Построение угла, равного данному. 7 класс.Скачать

Вопросы и ответы для 5-6 класса

1. Название какой цифры можно составить из букв слова СМАРТИК?

1. Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?

1. Предпоследнее число четвертого десятка — это

1. Смартик правильно заполнил схему на рисунке. В каких двух клетках оказались равные числа?

1. Сначала Смартик выписал в ряд четные числа из набора 1, 2, 3, 4, 5, 6, 7, 8, 9 в порядке убывания, а потом справа приписал нечетные числа в порядке возрастания. Какой фрагмент есть в его ряду?

1. В Цветочном городе коротышки учатся с понедельника по пятницу. Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял?

Ответ: А — 9 сентября

1. Три картонных прямоугольника 3 × 4 положили на клетчатый лист так, как показано на рисунке. Сколько клеток листа покрыто ровно двумя прямоугольниками?

1. Электронные часы показывают 22 : 20. Через какое время они покажут тот же набор цифр?

Ответ: В — через 4 часа 2 минуты

Задачи, оцениваемые в 4 балла

1. В турнире по теннису было 8 участников. Они разбились на пары и сыграли четыре матча, победители вновь разбились на пары и сыграли еще два матча. Наконец, победители этих матчей сыграли между собой финал. В этих семи матчах победили Вася, Аня, Миша, Аня, Толя, Аня, Миша (может быть, в другом порядке). Кто выиграл турнир?

Видео:Построение угла с помощью транспортираСкачать

Вопросы и ответы для 7-8 класса

Задачи, оцениваемые в 3 балла

1. В клетки квадрата на рисунке Смартик вписал последовательно буквы своего имени. Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?

1. Смартик решал уравнение. Он понял: чтобы найти х, нужно сначала вычесть из числа 12 число 4, а потом результат поделить на 2. Что это было за уравнение?

1. Смартик измерил два угла треугольника. Оказалось, что они равны 20° и 22°. Тогда этот треугольник

Ответ: Д — тупоугольный

1. Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?

1. Винни-Пух два дня подряд ходит в гости к Кролику, потом два дня подряд ходит в гости к Пятачку, потом снова два дня к Кролику и так далее. В воскресенье он был в гостях у Пятачка. В какой из дней на следующей неделе он наверняка ходил к Кролику?

Ответ: Б — вторник

1. На рисунке изображено несколько замкнутых линий. Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь?

1. Между какими двумя числами расположена дробь 2023/2022?

Ответ: В — 1,0001 и 1,001

1. Из цифр года 2022 можно составить ровно одну дату: 22.02, то есть 22 февраля. Через сколько лет будет год, из цифр которого тоже можно составить ровно одну дату?

Задачи, оцениваемые в 4 балла

1. У Маши есть 10 проволочных уголков (см. рисунок 1). Какое наименьшее число уголков нужно разогнуть, чтобы сложить контур, изображенный на рисунке 2?

На рисунке изображены три одинаковых квадрата. Чему равен отмеченный угол?

Чему равно наименьшее двузначное число, большее наибольшего двузначного числа, делящегося на 13?

Из города в Простоквашино в 14:00 выехал дядя Федор на велосипеде, и одновременно из Простоквашино выехал почтальон Печкин на тракторе. В 16:00 они встретились, а в 17:30 дядя Федор приехал в Простоквашино. Когда Печкин приехал в город?

На прямой отмечены точки А, В, С и D. Известно, что расстояние между А и В равно 2, между B и C — 3, а между С и D — 4 . Чему не может быть равно расстояние между А и D?

На какое наименьшее число нужно умножить 20²², чтобы получился куб натурального числа?

На сторонах равнобедренного треугольника ABC с основанием АС отмечены точки Е и D так, что BE=ED и AD=AC. Угол при вершине В равен 30°. Найдите угол EDA.

Видео:Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать

Вопросы и ответы для 9-10 класса

Задачи, оцениваемые в 3 балла

1. В день конкурса Смартик склеил бумажные буквы С и М (см. рисунок). Как может выглядеть его конструкция с другой стороны?

1. Карта страны Квадра поделена на 16 одинаковых квадратиков (см. рисунок). Какой из них является северо-западной частью юго-востока этой страны?

1. Семь чисел отмечены точками на числовой прямой. Произведение чисел P и Q равно одному из этих чисел. Какому?

1. Сколько дней в килосантинеделе?

1. Площади треугольников на рисунке равны 5 и 10, а прямые a, b и с параллельны. Расстояние между прямыми a и b равно 6. Чему равно расстояние между прямыми b и с?

1. Чему равна разность суммы чисел a и b и разности их суммы и разности?

1. Каждый день Вася ходит или на футбольную секцию, или на занятие математического кружка: 3 дня подряд — на футбол, потом 2 дня — на кружок, потом опять 3 дня — на футбол и так далее. В воскресенье он был на футболе. В какой из дней на следующей неделе он наверняка ходил на футбол?

Ответ: Д — пятница

1. Если 4a ∙ 8b = 16 c, то

Ответ: А — 2a+3b= 4 c

Задачи, оцениваемые в 4 балла

1. Диагональ квадрата равна квадрату стороны этого квадрата. Чему равна эта диагональ?

🔍 Видео

✓ Все сюжеты по планиметрии из ЕГЭ за 50 минут | ЕГЭ. Задание 16. Профильный уровень | Борис ТрушинСкачать

В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать