| Фигура | Рисунок | Формулировка | ||||||||
| Прямоугольный треугольник | ||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник |
| Равнобедренный прямоугольный треугольник |
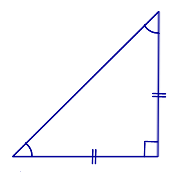 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . |
| Прямоугольный треугольник с углом в 30° |
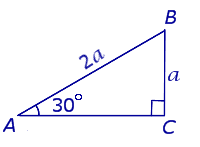 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
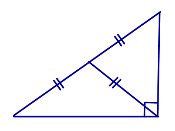 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Центр описанной окружности |
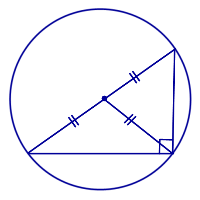 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
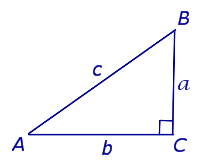 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным Содержание Видео:Найдите гипотенузу равнобедренного прямоугольного треугольника, площадь которого равна 1Скачать  Равнобедренный прямоугольный треугольник
Средняя оценка: 4.1 Всего получено оценок: 265. Средняя оценка: 4.1 Всего получено оценок: 265. И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно. Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать  ОпределениеРавнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны. Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания. Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать  СвойстваПоговорим подробнее о свойствах и формулах. Не совсем ясно, как будут проходить высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой. В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами. Если к гипотенузе прямоугольного равнобедренного треугольника провести высоту, то она разделит треугольник на два, равных между собой, равнобедренных прямоугольных треугольника. Теорема Пифагора для равнобедренного треугольника выглядит немного упрощенной: Квадрат гипотенузы равен удвоенному квадрату катета. Это значительно упрощает решение. Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками, решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника. Через гипотенузу можно найти катет и через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45. Разберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам. При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны. Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.е. 90 градусов, разделить пополам. Получается, что каждый из углов при гипотенузе прямоугольного равнобедренного треугольника будет равен 45 градусам. Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным. Из этого же свойства вытекает равенство синусов и косинусов острых углов прямоугольного равнобедренного треугольника между собой, а также равенство их тангенсов и котангенсов. То есть, синус любого острого угла прямоугольного равнобедренного треугольника равен косинусу любого острого угла данного треугольника и равен $$<sqrtover2>$$. Тангенс любого острого угла прямоугольного равнобедренного треугольника равен котангенсу любого острого угла данного треугольника и равен 1. Видео:Прямоугольный равнобедренный треугольникСкачать  Что мы узнали?Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника. А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике. Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия. Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать  Please wait.Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать  We are checking your browser. mathvox.ruВидео:№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать  Why do I have to complete a CAPTCHA?Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать  What can I do to prevent this in the future?If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 6d2cef395ccf2de6 • Your IP : 85.95.179.65 • Performance & security by Cloudflare 🔥 Видео№238. Докажите, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания,Скачать  Неравенства треугольника. 7 класс.Скачать  ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать  Высота, биссектриса, медиана. 7 класс.Скачать  Геометрия Найдите площадь равнобедренного прямоугольного треугольника, гипотенуза которого равна cСкачать  Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать  Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать  №412. Даны равнобедренный прямоугольный треугольник ABC с прямым углом С, катетом АС = 12 смСкачать 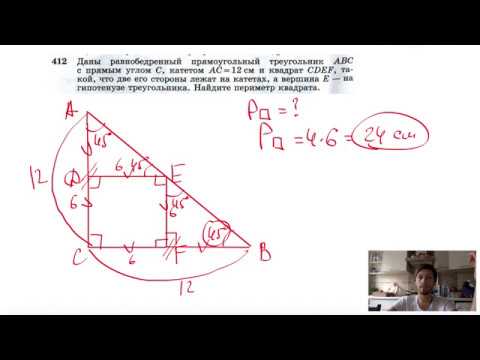 Равнобедренный треугольник. 7 класс.Скачать  Свойства прямоугольного треугольника. 7 класс.Скачать  Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать  |



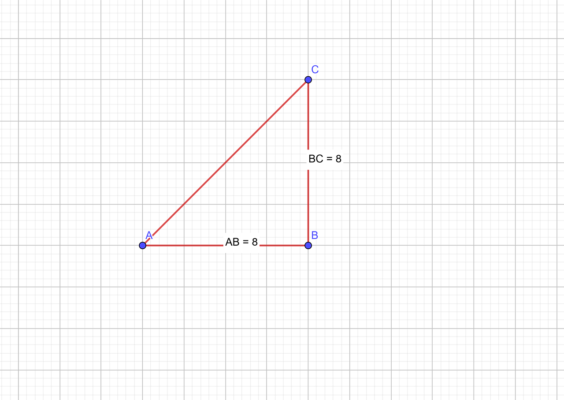 Рис. 2. Высота прямоугольного равнобедренного треугольника
Рис. 2. Высота прямоугольного равнобедренного треугольника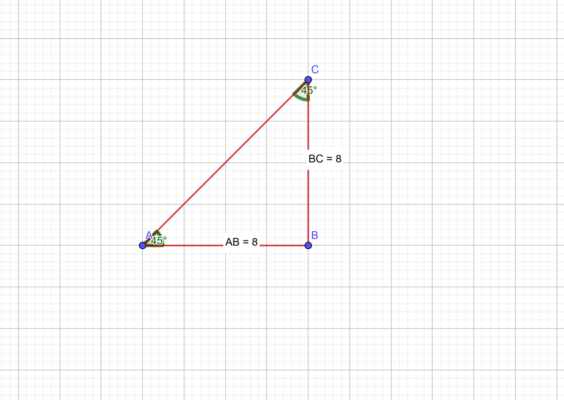 Рис. 3. Углы прямоугольного равнобедренного треугольника
Рис. 3. Углы прямоугольного равнобедренного треугольника