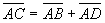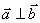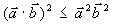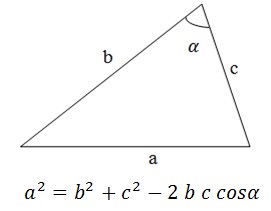Олимпиадные задачи на векторы (5 видео) | Курс школьной геометрии

Векторный метод при решении олимпиадных задач

Неоценима роль процесса решения задач в овладении умениями и навыками познавательного и практического характера. Развитие творческого мышления, самостоятельности, подготовка студентов к творческому труду возможны только при условии систематического решения задач.

Основная задача олимпиадного движения – пропаганда математических знаний среди молодежи, подготовка к будущей научной деятельности, заострение интеллекта. Чтобы студенты увлекались решением математических задач, необходимо их заинтересовать, а это сделать достаточно нелегко. Но если задача увлекательна, то интерес к ней, независимо от желания студента, мобилизует его умственную энергию, облегчает запоминание. Когда студент работает над теоретическим материалом, то усваивает чужие мысли, когда решает задачи, то мыслит самостоятельно. Польза от решения заключается не в отыскании ответа, а в том, что в процессе решения студент целенаправленно, последовательно совершенствует технику (закрепляет знание формул, алгоритмов, методов и приемов решений), развивает творческие способности. Элементы творчества на начальном этапе размышления над задачей переходят в технику решения на завершающем этапе[2]. Студентам специальности «Математика» в курсе изучения дисциплины «Практикум по решению математических задач» предлагаются решать задачи повышенной трудности, а также олимпиадные задачи. Покажем, как теоретический материал по применению векторного метода используется при решений олимпиадных задач.

Понятие вектора является одним из фундаментальных понятий современной математики. С помощью векторов могут быть решены содержательные геометрические задачи, причем их векторные решения часто значительно проще и эффективнее решений средствами элементарной геометрии. При решении задач находят применение сведения, известные из школьного курса геометрии: действие сложения векторов и его законы, вычитание векторов, действие умножения вектора на число и его законы, понятие коллинеарности векторов, разложение вектора в данном базисе, единственность разложения. Посредством этих действий и их свойств можно решать задачи на параллельность прямых, принадлежность трех точек одной прямой, вычисление отрезков параллельных прямых и некоторые другие. Однако задачи на вычисление расстояний и углов с помощью этих действий не могут быть решены. Для решения задач, связанных с длинами и углами (их называют метрическими), применяется скалярное умножение векторов и его свойства. Умение пользоваться векторным методом требует определенных навыков. Прежде всего необходимо хорошее знание теории. Надо научиться переводить геометрические соотношения между фигурами на векторный язык, а также, наоборот, полученные векторные соотношения истолковывать геометрически. Полезно запоминать некоторые, часто встречающиеся при решении задач векторные соотношения и обратить внимание на их большую общность.

Основные формулы и соотношения, используемые при решении задач.

1) Правило сложения векторов:.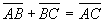

2) Правило вычитания векторов: , где О — произвольная точка.

3) Условие принадлежности трех точек А, В и С одной прямой:

a)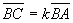; б) , где k — некоторое число.

5) Формула деления отрезка в данном отношении:

если , то 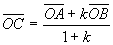, где О — произвольная точка.

6) Формула середины отрезка: если С — середина отрезка АВ, то .

При решении задач часто находит применение следующее свойство векторов:

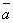
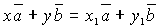
7) Единственность разложения вектора по двум неколлинеарным векторам: если векторы и неколлинеарны, то из равенства следует, что х = х₁и у= у₁

8) Если М и N — середины сторон АВ и CD четырехугольника ABCD, то .

а) 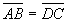; 6) ; в)

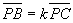
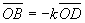
10) Если ABCD — трапеция с основанием АВ, стороны АО и ВС которой при продолжении пересекаются в точке Р, а диагонали – в точке О. то , и ,, где .

Особенностью векторных решений многих задач является то, что все привлекаемые для решения векторы откладываются от одной точки, удачный выбор которой часто позволяет упростить вычисления.

Многие геометрические задачи на вычисление расстояний и углов, на доказательство геометрических тождеств и неравенств могут быть решены при помощи скалярного произведения векторов.

По определению скалярного произведения векторов 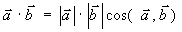, следовательно,

Равенство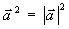 применяется для нахождения длины вектора.

Кроме этих формул и соотношений, для решения метрических задач используются также следующие:

11) Для ненулевых векторов и 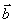:из следует, что

12) Для любых векторов и :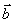

13) Для любых векторов 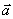и :

14) Для любых трех векторов , 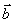и :

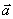
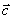
15) Для любых трех векторов , и :

16) Для любых трех точек A, В и С: 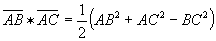Это равенство равносильно теореме косинусов.

17) Для любых четырех точек А, В, С и D:

Приведем пример использования векторного метода для решения задачи, которую можно решить и другими методами.

Из середины H основания BC равнобедренного треугольника ABC проведен перпендикуляр HE на сторону AC. Точка O – середина HE. Докажите, что отрезки BE и AO перпендикулярны.

Чтобы доказать перпендикулярность отрезков ВЕ и ОА, надо показать что скалярное произведение этих векторов равно нулю, т.е. ·=0.

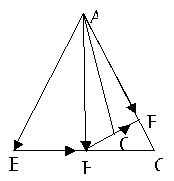
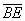
Выразим векторы =+ , = + , = + .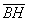

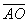
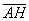
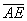
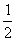
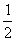
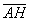
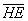
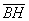
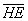
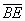
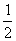
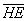
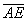
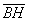
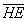
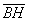
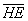
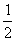
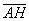
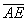
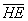
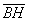
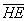
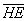
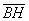
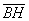
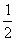
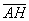
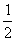
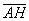
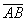
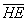
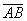
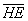
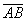
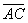
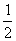
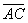
Найдем скалярное произведение, учитывая перпендикулярность векторв и , и , т.е · =0, · =0

· =( +)( +) = (· +· +· +· ) = =( ·+ ·) = (· +( +)) = = (· +· +· ) = (+ ) = (+ —) = = (2 —) = ( 2· +2· — ) = ·= 0.

Отсюда следует перпендикулярность отрезков ВЕ и ОА, что и требовалось доказать.

Векторный метод, как и любой другой, не является универсальным, хотя он и позволяет решать широкий круг геометрических задач.

1. Готман Э.Г. Задачи по планиметрии и методы их решения. М.: Просвещение: АО «Учеб.лит.», 1996.-240с.

2. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. М.: Айрис-пресс,2003.-432с.

Содержание

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1
Немного истории
Вступление
Немного теории о векторах
А теперь займемся практикой
Геометрические задачи на этапе подготовки к олимпиадам
📸 Видео

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1

Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.

Немного истории

Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.

В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).

Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».

Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.

Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.

Вступление

«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».

Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.

Немного теории о векторах

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.

Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.

Скалярное произведение векторов

Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)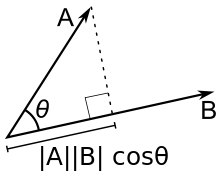

Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то скалярное произведение (a, b) = x₁x₂ + y₁y₂.

Косое произведение векторов

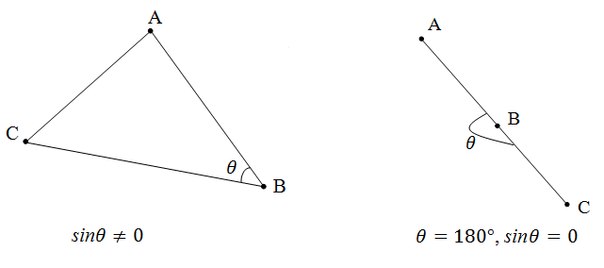
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то косое произведение [a, b] = x₁y₂ — x₂y₁.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.

А теперь займемся практикой

Начнем с треугольников

Задача №1

Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.

Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.

Задача №2

Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.

Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x₁, y₁), B(x₂, y₂) вычисляется по формуле √(x₁-x₂) 2 +(y₁-y₂) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.

Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.

Задача №3

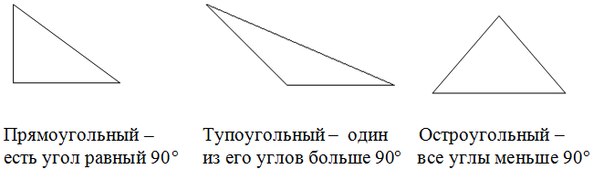
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.

Решение
Вспомним, что представляют собой каждый вид треугольника.

Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:

Угол больше 90° – треугольник тупоугольный
Угол меньше 90°– треугольник остроугольный
Угол равен 90°– треугольник прямоугольный

Воспользуемся теоремой косинусов:

Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:

Если cosα > 0, то a 2 2 + c 2 – треугольник остроугольный
Если cosα = 0, то a 2 = b 2 + c 2 – треугольник прямоугольный
Если cosα 2 > b 2 + c 2 – треугольник тупоугольный

где a – большая сторона.

Задача №4

Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.

Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.

Задача №5

По данным сторонам треугольника найти его площадь.

Решение
Очевидно решение, заключается в применение формулы Герона.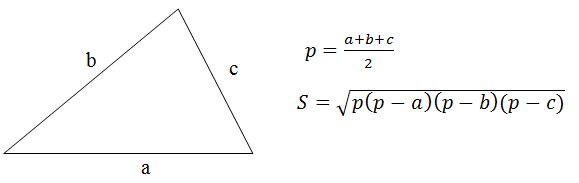

Кстати, никого не интересовало доказательство этой формулы?

Задача №6

Вычислить площадь треугольника заданного координатами своих вершин.

Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x₁, y₁), b(x₂, y₂)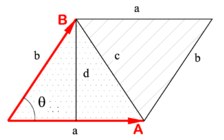

S = (x₁y₂ — x₂y₁) / 2 — ориентированная площадь треугольника

Задача №7

Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.

Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.

Метод площадей

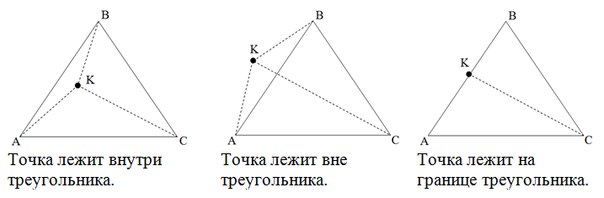
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.

Проверка полуплоскостей

Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.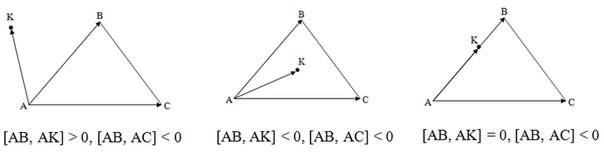

В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.

Задача №8

Вычисление площади многоугольника заданного координатами своих вершин.

Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.

Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.

Метод трапеций

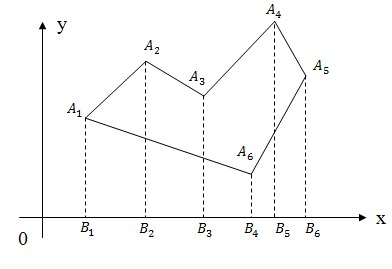
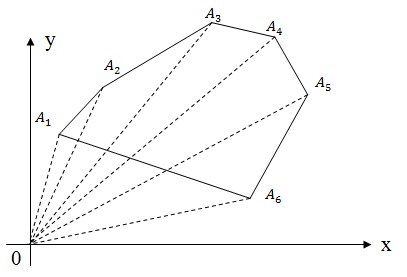
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = S_A₁ _A₂ _B₂ _B₁ + S_A₂ _A₃ _B₃ _B₂ + S_A₃ _A₄ _B₅ _B₃ + S_A₄ _A₅ _B₆ _B₅ + S_A₅ _A₆ _B₄ _B₆ + S_A₆ _A₁ _B₁ _B₄
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
S_A₁ _A₂ _B₂ _B₁ = 0.5 * (A₁B₁ + A₂B₂) *(B₂ — B₁)

Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.

Метод треугольников

Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.

Задача №9

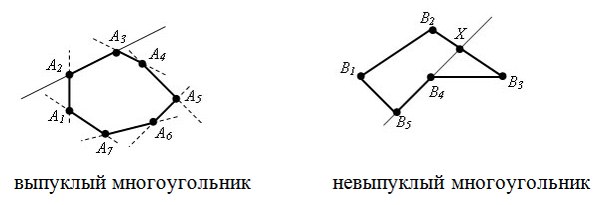
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.

Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [A_i A_i+1, A_i+1 A_i+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.

Задача №10

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

Решение
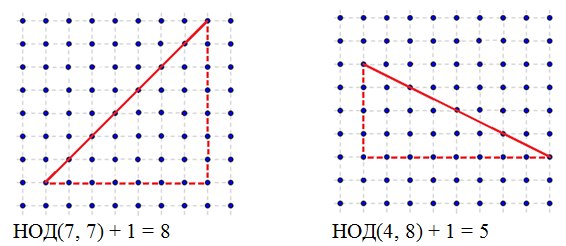
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.

Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример: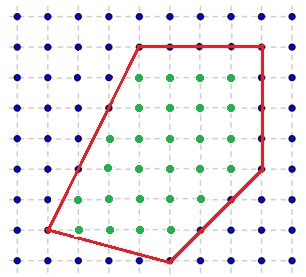

S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!

Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Геометрические задачи на этапе подготовки к олимпиадам

Статистика итогов математических олимпиад различного уровня показывает, что к решению геометрических задач приступают буквально единицы конкурсантов. Даже решение простых задач из школьного учебника вызывает затруднения у многих учащихся.
Чтобы приобщить учащихся к решению геометрических задач, убедить их в полезности таких занятий, необходимо уделять внимание разбору геометрических задач на уроках математики в 5 – 6 классах, на внеурочных занятиях, на этапе подготовки к олимпиадам.
Олимпиадные геометрические задачи полезны не только для проверки математических способностей и уровня математической подготовленности учащихся в жестких соревновательных условиях. На занятиях математического кружка, в спокойной обстановке, конкурсная задача является источником небольшого самостоятельного исследования, творческого открытия. Известный педагог-математик Д. Пойа писал: «Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».
Необходимо как можно раньше начинать работать с детьми по развитию математических способностей, вызывать интерес к предмету, побуждать ребят к систематическим занятиям математикой. Поэтому я с 5 класса веду математический кружок, привлекаю учащихся к участию в олимпиадах и конкурсах различного уровня (школьный, районный тур олимпиад, республиканский этап математической олимпиады Junior math, международный математический конкурс «Кенгуру», различные интернет-олимпиады). Интересно, что ребята включаются в этот марафон, переживают за неудачи, радуются своим успехам, сравнивая предыдущие результаты с новыми и наблюдая «рост». Главное, разжечь в них соревновательный дух, который послужит важным стимулом к дальнейшим целенаправленным занятиям.
Для расширения кругозора и конструктивных навыков хороши практические задания, связанные с разрезаниями, проведениями построений. В таких задачах не используются знакомые алгоритмы решения, они требуют нестандартного подхода. Необходимо учить ребят находить пути к решению проблемы, а это значит – формировать у них способность к самостоятельному, творческому мышлению.
Представляю разработку кружкового занятия по теме «Решение геометрических задач». Занятие может быть организовано как для учащихся 5 – 6 классов, так и для более старших школьников. Главной целью его является приобщение учащихся к миру математики, убеждение учащихся в том, что размышление, рассуждение, выдвижение идей приводит к удивительным и полезным открытиям. Занятие построено так, что рассматривая задачи различного уровня и содержания, учащиеся постепенно, от простого к сложному, продвигаются в своем развитии, совершенствуют навыки решения олимпиадных задач. Разнообразные теоретические факты вытекают из практических упражнений и экспериментов. Это занятие составлено в соответствии с авторской модульной программой работы с математически способными детьми. Использованы задачи из различных сборников олимпиадных заданий:

Евдокимов М.А. От задачек к задачам. М.: МЦНМО, 2004
Игнатьев Е.И. В царстве смекалки. М.: «Наука», 1987
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М.: «Просвещение», 1988
Материалы международного конкурса «КЕНГУРУ»

Методическая разработка занятия математического кружка

Класс:
5 – 6
Тема:
Решение геометрических задач

Цели:

развивать пространственное воображение, конструкторские навыки;
способствовать развитию интереса к предмету;
учиться ведению логически стройного доказательства;
способствовать самореализации и самосовершенствованию каждого ученика.

Оборудование:

карточки с заданиями;
наглядные иллюстрации к задачам;
сборники олимпиадных заданий;
материалы международного математического конкурса «КЕНГУРУ»;
бумага, ножницы для практических экспериментов.

Этапы занятия:

Организационные моменты (1 мин)
Разминка (5 мин)
Разбор интересных задач на проведение линий, разбиение фигур, перекраивания (20 мин)
Решение задач математического конкурса «Кенгуру» (15 мин)
Творческое домашнее задание (2 мин)
Подведение итогов занятия (2 мин)

Ход занятия:

1 этап. (Организационный)
Учитель: – Для работы разобьемся на группы, чтобы вам было интереснее работать с товарищами. Постарайтесь быть активными, полезными для своей команды. Вносите свои предложения, прислушивайтесь к мнению других.
(Класс разбивается на группы, в составе которых оказываются учащиеся с разной математической подготовкой. Это необходимо для того, чтобы каждый нашел себе применение, и «слабый» имел возможность тянуться за «сильным»)

II этап. Разминка
1) Учащиеся получают три рисунка:

Вопросы:
Сравните длины отрезков на рисунках 1 и 2. На сколько сантиметров один отрезок больше другого?
Сравните длины диагоналей параллелограммов на рисунке 3. У какого параллелограмма диагональ длиннее? (Для учащихся 5 – 6 классов пояснить, что называют параллелограммом, его диагоналями).
(После обсуждения в группах учащиеся высказывают предположения. Затем непосредственным измерением отрезков выясняют, правы ли они. Почему возникает такая иллюзия, что один отрезок кажется длиннее другого?)
2) Как, не отрывая карандаша от бумаги, разделить фигуру на рисунке 2 на шесть равных треугольников?

Рисунок 2. Рисунок 3. Рисунок 4.

III этап.Разбор интересных задач на проведение линий, разбиение фигур, перекраивания.
Задача 1
Постройте замкнутую ломаную линию, состоящую из трех звеньев и проходящую через четыре данные точки (Рисунок 3).
Задача 2
Как ломаной линией, состоящей из четырех отрезков, не отрывая карандаша от бумаги, перечеркнуть девять точек, расположенных так, как показано на рисунке 4?
(Обсудить все предложенные ребятами варианты решения. Обратить внимание учащихся на то, что задача считается решенной, если выполнены все требования условия, то есть ломаная состоит из четырех звеньев, звенья ломаной не должны накладываться друг на друга, линия должна быть без разрывов).
Задача 3
Как тремя прямолинейными разрезами разделить круглый торт на:
а) семь,
б) восемь частей (Рисунок 5)?

Возможные варианты решения (Рисунок 6, Рисунок 7):

Рисунок 6. Рисунок 7.

Задача 4

Как из набора «уголков» сложить прямоугольник (Рисунок 8)?
Решение:
Подсчитаем, какую площадь займут все «уголки» 3+4+5+6+7+8=11*3=33. Значит, стороны прямоугольника могут быть равны 3 и 11. Остается заполнить прямоугольник 3*11 данными «уголками». Например, как на рисунке 9:

Задача 5
Разрежьте фигуру на две части и сложите из них квадрат (Рисунок 10).

Вопросы для обсуждения:
– Какова площадь первоначальной фигуры?
12*9-8=108-8=100
– Значит, сложив части, мы получим квадрат размером 10*10.
– На сколько нужно увеличить сторону длиной 9 клеток и на сколько уменьшить другую сторону? (на 1 и на 2)
Вариант разрезания (Рисунок 11):

IV этап. Решение задач математического конкурса «Кенгуру»
Задачи «Кенгуру»

Решение: Заметим, что линия, составленная из горизонтальных и вертикальных отрезков, имеет наибольшую длину.
Сравним (Рисунок 13)

Таким образом, в порядке убывания длины: (D) – (C) – (A) или (E) – (B).
Самая короткая линия – В.
Для того, чтобы покрасить кубик, изображенный на левом рисунке (Рисунок 14), понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображенную на правом рисунке?

(А) 4 кг (В) 5 кг (С) 6 кг (Д) 9 кг (Е) 12 кг
Решение: Площадь поверхности первой фигуры равна 9*6=54, правой – 9+9+9+5+5+5+12=54. Так как площади равны, то краски понадобится столько же, т.е. 9 кг.
Если бумажный кубик разрезать по некоторым ребрам и развернуть, то получится развертка I (Рисунок 15), а если стереть некоторые буквы и потом разрезать кубик иначе, получится развертка II. Какая буква стояла на месте вопросительного знака?

(A) А (B) В (C) С (D) Е (E) невозможно определить

Решение: «Соберем» первый (Рисунок 16) кубик и расставим на нем буквы (можно использовать модель кубика)

Рисунок 16. Рисунок 17.

Перевернем его на себя (Рисунок 17):
Если полученный кубик разрезать, то на месте вопросительного знака , то есть справа от D , будет буква Е.
Ответ: (D)
V этап.Творческое домашнее задание

У одной хозяйки было два клетчатых коврика: один размером 60х60 см, другой 80х80 см. Она решила сделать из них один клетчатый коврик размером 100х100 см. Мастер взялся выполнить эту работу и пообещал, что каждый коврик будет разрезан не более чем на две части и при этом не будет разрезана ни одна клетка. Обещание свое он сдержал. Как он поступил?
Изображенную на рисунке 18 фигуру требуется разделить на 6 частей, проведя всего лишь 2 прямые. Как это сделать?

VI этап. Подведение итогов занятия.

Узнали ли вы сегодня на занятии что-то новое? Что именно?
Понравилась ли вам работа в группах? Какую роль в группе играли вы? (Активно обсуждал, предлагал идеи, слушал других, старался не привлекать к себе внимания и т.п.)
Какие интересные элементы можно добавить в организацию занятия?

Ответы ребят помогут учителю оценить проведенное занятие, спланировать дальнейшую работу.