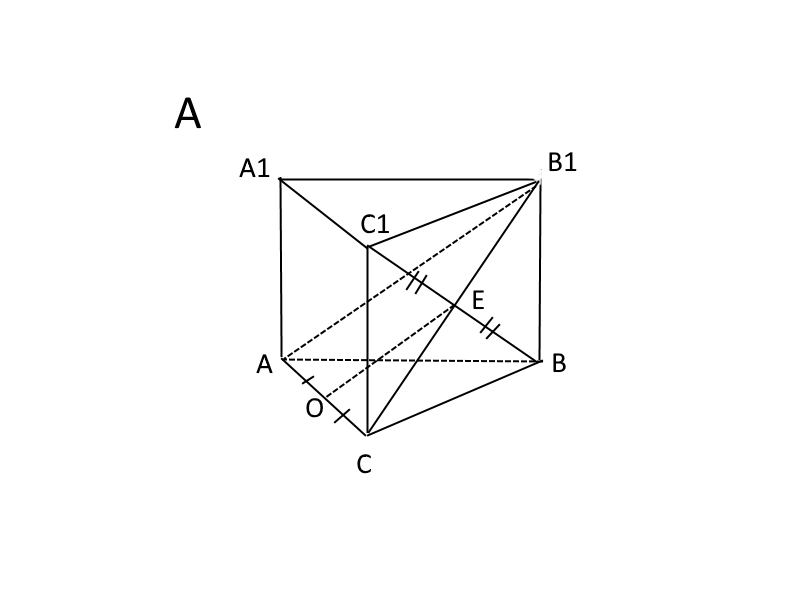
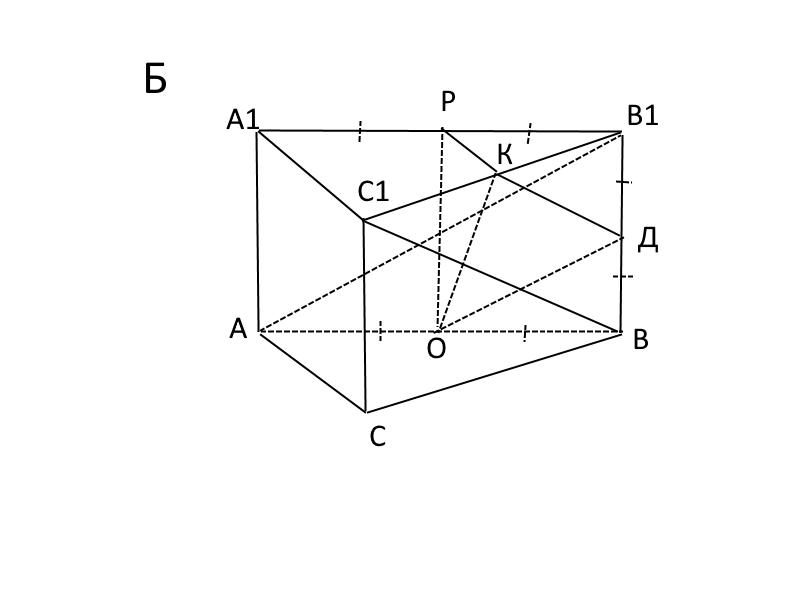
В правильной треугольной призме abca1b1c1 все ребра равны 1 докажите что ab1 параллельна прямой

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:Задача №14 ЕГЭ профиль геометрия. В правильной треугольной призме ABCA1B1C1Скачать

Задача 11035 В правильной треугольной призме.

Условие

В правильной треугольной призме АВСА1В1С1 все рёбра равны 1.

а) Докажите, что прямая АВ1 параллельна прямой, проходящей через середины отрезков АС и ВС1.
б)Найдите косинус угла между прямыми АВ1 и ВС1.

Решение

А) О – середина АС, Е – серединаВС1
Так как все ребра правильной призмы равны 1, то боковые грани являются квадратами, то есть Е – точка пересечения диагоналей квадрата и СЕ=ЕВ1.
Тогда ОЕ – средняя линия треугольника В1СА, = > ОЕ||АВ1.

Б) Пусть О – середина АВ, Д – середина ВВ1.
Проведем прямую параллельную прямой АВ1 через точку О в треугольнике АВВ1, ОД||АВ1, = > ОД-средняя линия треугольника АВВ1. ОД=1/2АВ1
АВ1=ВС1=sqrt(1+1)=sqrt(2) (по теореме Пифагора)
ОД= sqrt(2)/2
Проведем прямую параллельную прямой ВС1 через точку Д в треугольнике ВВ1С1, ДК||ВС1, ДК – средняя линия треугольника ВВ1С1. ДК=1/2ВС1= sqrt(2)/2.
Значит, угол ОДК – искомый угол между скрещивающимися прямыми АВ1 и ВС1.
ОР||АА1, ОР перпендикулярен основаниям, = > ОР⊥РК, тогда треугольник ОРК — прямоугольный.
РК=1/2А1С1=1/2, OP=AA1=1
По теореме Пифагора, получаем: ОК=sqrt(1+1|4)=sqrt(5)/2
По теореме косинусов из треугольника ОДК:
ОД^2+КД^2-2ОД*КД*cosОДК=ОК^2
1/2+1/2-2* sqrt(2)/2* sqrt(2)/2 *cosОДК=5/4
1- cosОДК=5/4
cosОДК=-1/4
Так как косинус получился отрицательный, то мы нашли тупой угол. Значит надо найти cos острого угла между прямыми.
Он равен cos(180-α)=-cosα=1/4.

Видео:ЕГЭ 2017. Стереометрия. Угол между скрещивающимися прмыми. Пример из" варианты Ященко".Скачать

В правильной треугольной призме abca1b1c1 все ребра равны 1 докажите что ab1 параллельна прямой

БАЗА ЗАДАНИЙ

Задание № 13. Стереометрия с доказательством.

1. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите угол наклона плоскости α к плоскости грани BB ₁ C ₁ C.

2. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

4. В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2

5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3

7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Ответ: б) 2,4

8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.

9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9. Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
а) Докажите, что плоскость CEF параллельна ребру SB.

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

10. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона основания AB равна 6, а боковое ребро AA ₁ равно 2√2. На рёбрах AB, A ₁ B ₁ и B ₁ C ₁ отмечены точки M, N и K соответственно, причём AM = B ₁ N= C ₁ K=2.
а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Ответ: б) 15

11. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 6, а боковое ребро AA ₁ =3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A ₁ C ₁ и B ₁ C ₁ соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4

12. В правильной четырёхугольной призме ABCDA ₁ B ₁ C ₁ D ₁ сторона AB основания равна 8, а боковое ребро AA ₁ равно 4√2. На рёбрах BC и C ₁ D ₁ отмечены точки K и L соответственно, причём BK= C ₁ L=2. Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A ₁ C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.

13. В основании прямой треугольной призмы ABCA ₁ B ₁ C ₁ лежит равнобедренный (AB=BC) треугольник ABC. Точка K— середина ребра A ₁ B ₁ , а точка M делит ребро AC в отношении AM:MC=1:3.
а) Докажите, что KM⊥AC.
б) Найдите угол между прямой KM и плоскостью ABB ₁ , если AB=6, AC=8, AA ₁ = 3.

14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB=2√2, AD=6, AA₁=10. На рёбрах AA₁ и BB₁ отмечены точки E и F соответств., причём A ₁ E:EA =3:2 и B ₁ F:FB=3:7. Точка T — середина ребра B ₁ C ₁ .
а) Докажите, что плоскость EFT проходит через точку D ₁ .
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Ответ: б) 22,5

а) Докажите, что плоскость EFT проходит через вершину D₁.

б) Найдите угол между плоскостью EFT и плоскостью AA₁B₁.

16. На ребрах CD и BB1 куба ABCDA₁B₁C₁D₁ c ребром 12 отмечены точки Р и Q соответственно, причем DP=4, а B ₁ Q=3. Плоскость APQ пересекает ребро CC ₁ в точке М.
а) Докажите, что точка М является серединой ребра CC ₁ .
б) Найдите расстояние от точки С до плоскости APQ.

17. В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM=DN=4 и АК=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.

18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.

19. Основанием прямой четырехугольной призмы ABCDA ₁ B ₁ C ₁ D ₁ является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA ₁ в соотношении AK:KA ₁ =1:2. Через точки K и B проведена плоскость α, параллельная прямой AC и пересекающая ребро DD ₁ в точке M.
а) Докажите, что плоскость α делит ребро DD ₁ в отношении DM:MD ₁ =2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6

20. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 12, а боковое ребро AA ₁ равно 3√6. На ребрах AB и B ₁ C ₁ отмечены точки K и L соответственно, причем AK=2, B ₁ L=4. Точка M середина A ₁ C ₁ . Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2

21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 и BC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30

22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=AQ=RC=2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2

23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90

24. Основанием прямой треугольной призмы ABCA ₁ B ₁ C ₁ является прямоугольный треугольник ABC с прямым углом C. Прямые CA ₁ и AB ₁ перпендикулярны.
а) Докажите, что AA ₁ =AC.
б) Найдите расстояние между прямыми CA ₁ и AB ₁ , если AC = 6, BC = 3.
Ответ: б) √2

6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

3. Сечением прямоугольного параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ плоскостью α, содержащей прямую BD ₁ и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.
б) Найдите угол между плоскостями α и BCC ₁ , если AA ₁ =10, AB=12.

База заданий сформирована из Официального Банка заданий ФИПИ,

Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.

🔍 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Задача 14 (С2) из проф ЕГЭ 2017 по математикеСкачать

В правильной треугольной призме сторона основания равнаСкачать

Угол между прямыми Треугольная призмаСкачать

Стереометрия 23 | mathus.ru | угол между плоскостями в правильной треугольной призмеСкачать

Стереометрия, номер 10.1Скачать

№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что АС1 = 2ВС. Найдите угол междуСкачать

№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1.Скачать

№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

14-я задача ЕГЭ по математике. Видеоурок №4Скачать

ЕГЭ 2022 Математика Задание №13 Вариант 5 Профильный ур. Стереометрия Призма ЯщенкоСкачать

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

ЕГЭ 2022 Математика Задание №13 Вариант 3 Профильный ур. Стереометрия Призма. ЯщенкоСкачать

№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать