Скачать
презентацию
Задача №5. В параллелограмме лежат две окружности, касающиеся друг друга и трех сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен . Найдите площадь параллелограмма.
Слайд 26 из презентации «Задачи на параллелограмм». Размер архива с презентацией 370 КБ.
Видео:№9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости αСкачать

Геометрия 10 класс
«Сечение многогранников» — Основные виды сечений многогранников. Определения. Постройте сечение тетраэдра. Метод следов. Разделите каждую изучаемую вами задачу. Методы построения сечений. Сечения многогранников. План построения линий пересечения плоскостей. Правила для самоконтроля. Сечениями.
«Примеры симметрии в природе» — Виды симметрии. Симметрия в географии. Симметрия в биологии. Природные объекты. Симметрия является фундаментальным свойством природы. Симметричные фигуры. Симметрия в геологии. Человек, многие животные и растения обладают двусторонней симметрией. Что такое симметрия. Примеры симметричного распределения. Симметрия внешней формы кристалла. Симметрия в природе. Симметрия в физике. Дискретная симметрия.
«Параллельность плоскостей» — Проверяем свою работу. Плоскости называются параллельными, если они не пересекаются. Теоремы. Параллельные плоскости в быту. Признак параллельности. Плоскости параллельны. Доказательство от противного. Параллельный мир. Середины. Могут ли прямая и плоскость не иметь общих точек. Невозможные фигуры возможны. Параллельность плоскостей. Невозможные структуры. Параллельные плоскости в природе. Плоскости.
«Сечения фигур» — Многогранники в архитектуре. Искомое сечение. Решение. Пирамида. Точка. Глубины различных наук. Земля. Отметим точки. Определение. Проведем прямую. Построить сечение куба. Построение сечений многогранника. Сечение пирамид. Воздух. Сечение. Постройте сечение пирамиды. Сечение куба плоскостью. Точка пересечения прямых. Значение. Примеры построений сечений. Пчёлы. Точки, лежащие в плоскости сечения. Прямые в плоскостях.
«Основные аксиомы стереометрии» — Геометрия. Первые уроки стереометрии. Основные фигуры в пространстве. Следствия из аксиом. Источники и ссылки. Геометрические тела. Изображения пространственных фигур. Аксиома. Точки прямой лежат в плоскости. Четыре равносторонних треугольника. Следствия из аксиом стереометрии. Пирамида Хеопса. Предмет стереометрии. Плоскость. Плоскости имеют общую точку. Древняя китайская пословица. Аксиомы стереометрии.
««Параллельность плоскостей» 10 класс» — Пересекающиеся прямые m и n плоскости параллельны плоскости. Отрезки параллельных прямых. Признак параллельности трех плоскостей. Докажите, что плоскости ЕКМ и АВС параллельны. Пересекающиеся в точке М прямые a и b. Свойство параллельных плоскостей. Признак параллельности двух плоскостей. Прямая A пересекает плоскости. Параллельность. Найдите взаимное положение прямых. Докажите, что плоскости МЕР и АВС параллельны.
Всего в теме «Геометрия 10 класс» 54 презентации
Видео:Сможешь найти площадь параллелограмма? Внутри него есть две окружностиСкачать

В параллелограмме лежат две окружности касающиеся
В параллелограмме ABCD расположены две равные непересекающиеся окружности. Первая касается сторон AD, AB и BC, вторая — сторон AD, CD и BC.
а) Докажите, что общая внутренняя касательная l окружностей проходит через точку пересечения диагоналей параллелограмма ABCD.
б) Пусть ABCD — прямоугольник, а прямая l касается окружностей в точках M и N. Найдите площадь четырёхугольника с вершинами в точках M, N и в центрах окружностей, если AD = 36 , а расстояние между центрами окружностей равно 20.
а) Пусть O — точка пересечения диагонали AC параллелограмма с общей внутренней касательной l к данным окружностям, P и Q — точки пересечения прямой l со сторонами AD и BC соответственно. Достаточно доказать, что O — середина диагонали AC.
Пусть O1 и O2 — центры первой и второй окружностей соответственно. Первая окружность касается стороны AD в точке K, вторая окружность касается стороны BC в точке L.
Лучи AO1 и CO2 — биссектрисы равных углов BAD и BCD, значит, прямоугольные треугольники AKO1 и CLO2 равны по катету (радиусы равных окружностей) и противолежащему острому углу. Тогда AK = CL. Аналогично KP = LQ. Следовательно,
Значит, треугольники AOP и COQ равны по стороне и двум прилежащим к ней углам, поэтому AO = OC, а точка O — середина диагонали AC, то есть центр параллелограмма ABCD.
б) Поскольку ABCD — прямоугольник, его сторона AD равна сумме диаметра окружности и отрезка O1O2, то есть 2r + O1O2 = AD, 2r + 20 = 36, следовательно, r = 8.
Четырёхугольник O1MO2N — параллелограмм, так как его противоположные стороны O1M и O2N равны и параллельны. Диагонали O1O2 и MN параллелограмма O1MO2N пересекаются в точке O и делятся этой точкой пополам.
Площадь параллелограмма O1MO2N в четыре раза больше площади треугольника OO1M, в котором
По теореме Пифагора
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:3.27.1. Планиметрия. Гордин Р.К.Скачать 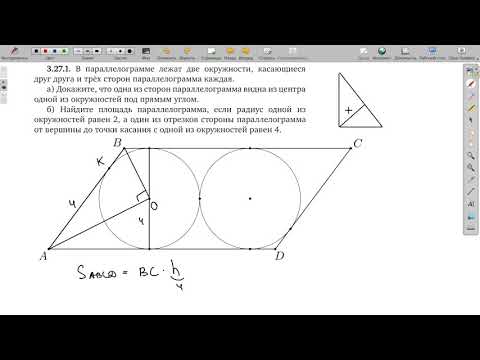 В параллелограмме лежат две окружностиВидео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Найдите площадь параллелограммаСкачать | |
| Окружности равны >> |
Задача №5. В параллелограмме лежат две окружности, касающиеся друг друга и трех сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен . Найдите площадь параллелограмма.
Слайд 26 из презентации «Задачи на параллелограмм». Размер архива с презентацией 370 КБ.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия 10 класс
«Сечение многогранников» — Основные виды сечений многогранников. Определения. Постройте сечение тетраэдра. Метод следов. Разделите каждую изучаемую вами задачу. Методы построения сечений. Сечения многогранников. План построения линий пересечения плоскостей. Правила для самоконтроля. Сечениями.
«Примеры симметрии в природе» — Виды симметрии. Симметрия в географии. Симметрия в биологии. Природные объекты. Симметрия является фундаментальным свойством природы. Симметричные фигуры. Симметрия в геологии. Человек, многие животные и растения обладают двусторонней симметрией. Что такое симметрия. Примеры симметричного распределения. Симметрия внешней формы кристалла. Симметрия в природе. Симметрия в физике. Дискретная симметрия.
«Параллельность плоскостей» — Проверяем свою работу. Плоскости называются параллельными, если они не пересекаются. Теоремы. Параллельные плоскости в быту. Признак параллельности. Плоскости параллельны. Доказательство от противного. Параллельный мир. Середины. Могут ли прямая и плоскость не иметь общих точек. Невозможные фигуры возможны. Параллельность плоскостей. Невозможные структуры. Параллельные плоскости в природе. Плоскости.
«Сечения фигур» — Многогранники в архитектуре. Искомое сечение. Решение. Пирамида. Точка. Глубины различных наук. Земля. Отметим точки. Определение. Проведем прямую. Построить сечение куба. Построение сечений многогранника. Сечение пирамид. Воздух. Сечение. Постройте сечение пирамиды. Сечение куба плоскостью. Точка пересечения прямых. Значение. Примеры построений сечений. Пчёлы. Точки, лежащие в плоскости сечения. Прямые в плоскостях.
«Основные аксиомы стереометрии» — Геометрия. Первые уроки стереометрии. Основные фигуры в пространстве. Следствия из аксиом. Источники и ссылки. Геометрические тела. Изображения пространственных фигур. Аксиома. Точки прямой лежат в плоскости. Четыре равносторонних треугольника. Следствия из аксиом стереометрии. Пирамида Хеопса. Предмет стереометрии. Плоскость. Плоскости имеют общую точку. Древняя китайская пословица. Аксиомы стереометрии.
««Параллельность плоскостей» 10 класс» — Пересекающиеся прямые m и n плоскости параллельны плоскости. Отрезки параллельных прямых. Признак параллельности трех плоскостей. Докажите, что плоскости ЕКМ и АВС параллельны. Пересекающиеся в точке М прямые a и b. Свойство параллельных плоскостей. Признак параллельности двух плоскостей. Прямая A пересекает плоскости. Параллельность. Найдите взаимное положение прямых. Докажите, что плоскости МЕР и АВС параллельны.
Всего в теме «Геометрия 10 класс» 54 презентации
Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Задача про две окружности в параллелограмме
а) В параллелограмме (ABCD) расположены две равные непересекающиеся окружности. Первая касается сторон (AD), (AB) и (BC), вторая сторон (AD), (CD) и (BC).
б) Пусть (ABCD) – прямоугольник, а прямая (l) касается окружностей в точках (M) и (N). Найдите площадь четырёхугольника с вершинами в точках (M), (N) и в центрах окружностей, если (AD=36), а расстояние между центрами окружностей равно (20).
а) В параллелограмме (ABCD) расположены две равные непересекающиеся окружности. Первая касается сторон (AD), (AB) и (BC), вторая сторон (AD), (CD) и (BC).
1) У параллелограмма точка пересечения диагоналей – это точка, в которой диагонали делятся пополам.
2) Диагональ и касательная (l) обязательно пересекаются в какой-то точке, поскольку очевидно не параллельны. Значит, если доказать, что касательная делит диагональ пополам, то можно говорить о том, что касательная проходит через точку пересечения диагоналей.
3) Как же доказать, что (AK=KC)? Один из самых популярных способов доказать, что отрезки равны – доказать равенство треугольников, в которых эти отрезки являются, например, сторонами. В нашем случае это (∆AKF) и (∆EKC).
4) Как доказать, что (∆AKF=∆EKC)? С углами всё хорошо — все три пары углов в этих треугольниках равны либо как вертикальные, либо как накрест лежащие. А вот со сторонами сложнее. Нужно доказать либо (EK=KF), либо (AF=EC).
5) Есть ощущение, что (AH_1=H_2 C) и (EH_2=H_1 F). Но ощущений маловато, нужно что-то посерьезнее… Вспомним, что это отрезки касательных, а где есть касание, там зачастую правильным действием будет провести радиус в точку касания. И соединим еще центры окружностей с (F) и (E), чтоб получились треугольники.
6) Можно ли доказать, что (∆O_1 FH_1=∆O_2 EH_2)? Есть прямые углы между радиусами и сторонами параллелограмма (ведь эти стороны – касательные к окружности). Есть радиусы, и они равны, так как по условию задачи окружности равные. Нужно равенство еще одной пары сторон или углов.
7) Попробуем доказать, что (∠H_1FO_1=∠H_2 EO_2).
Заметим, что (∠AFE=∠FEC) как накрест лежащие. При этом окружность с центром (O_1) вписана в угол (AFE), то есть (FO_1) – биссектриса. И с (EO_2) аналогично! Тогда получается, то (∠H_1 FO_1=∠H_2 EO_2) как половинки от равных углов (∠AFE=∠FEC)!
8) Супер! Последний кусочек найден, теперь можно собирать весь паззл.
(∆O_1 FH_1=∆O_2 EH_2) по катету и острому углу: (∠H_1 FO_1=∠H_2 EO_2), (O_1 H=O_2 H) как радиусы. Значит (H_1 F=EH_2).
9) Аналогично можно доказать равенство (∆O_1 H_1 A=∆O_2 H_2 C) из которого сделать вывод (AH_1=H_2 C).
10) (AF=AH_1+H_1 F=H_2 C+EH_2=EC),
(∠KAF=∠KCE) (как накрест лежащие),
(∠KFA=∠KEC) (аналогично).
Следовательно, (∆AKF=∆EKC), а значит и (AK=KC).
11) Получается касательная проходит через середину диагонали, а значит и через точку пересечения диагоналей.
1) Обозначим точку пересечения касательной (l) и диагонали (AC) как (K), точки касания окружностями сторон параллелограмма — (H_1) и (H_2), точки пересечения касательной и сторон параллелограмма — (E) и (F).
2) (∠H_1 FO_1=∠H_2 EO_2): (∠AFE=∠FEC) как накрестлежащие, (FO_1) и (EO_2) – биссектрисы по свойству вписанной окружности, значит (∠H_1 FO_1=frac ∠AFE=frac ∠FEC=∠H_2 EO_2).
3) Радиусы двух окружностей равны, так как окружности равные по условию задачи.
4) (∆O_1 FH_1=∆O_2 EH_2) по катету и острому углу: (∠H_1 FO_1=∠H_2 EO_2), (O_1 H_1=O_2 H_2) (как радиусы), (∠O_1 H_1 F=∠O_2 H_2 E=90^°) (как углы между касательными и радиусами, проведенными в точку касания). Значит (H_1 F=EH_2).
5) Аналогично можно доказать равенство (∆O_1 H_1 A=∆O_2 H_2 C) из которого сделать вывод (AH_1=H_2 C).
6) Таким образом имеем: (AF=AH_1+H_1 F=H_2 C+EH_2=EC), (∠KAF=∠KCE), (∠KFA=∠KEC) (как накрест лежащие). Следовательно, (∆AKF=∆EKC), а значит (AK=KC).
7) Точка пересечения диагоналей параллелограмма – это их общая середина, а т.к. касательная (l) проходит через середину (AC), то она проходит и через точку пересечения диагоналей.
Что и требовалось доказать.
б) Пусть (ABCD) – прямоугольник, а прямая (l) касается окружностей в точках (M) и (N). Найдите площадь четырёхугольника с вершинами в точках (M), (N) и в центрах окружностей, если (AD=36), а расстояние между центрами окружностей равно (20).
1) (MN) — касательная, (O_1 M) — радиус. Значит угол между ними — (90^°). Получается (∆MNO_1) прямоугольный. Треугольник (∆MNO_2) точно такой же, и если найти его площадь, то можно будет умножить её на (2) и найти площадь всего четырехугольника.
2) Давайте проведем радиусы к нижней стороне и к боковым сторонам прямоугольника.
3) Очевидно, что получилось два равных квадрата и их стороны можно найти: (AT=LD=frac =frac =8). Тогда радиус тоже равен (8).
4) Заметим, что (O_2 N∥O_1 M) (ведь они оба перпендикулярны одной и той же прямой MN) и (O_2 N=O_1 M), следовательно (O_1 MO_2 N) – параллелограмм. А значит диагонали точкой пересечения делятся пополам и (O_2 K=frac O_1 O_2=10).
5) Получается (KN=sqrt =6), а (MN=6cdot 2=12).
6) (S_ =frac MNcdot MO_1=frac cdot 12cdot 8=48).
1) (O_2 N⊥MN) и (O_1 M⊥MN) как радиусы, проведенные в точку касания. Значит (O_2 N∥O_1 M). К тому же, (O_2 N=O_1 M) как радиусы равных окружностей. Следовательно, (O_1 MO_2 N) – параллелограмм.
2) (O_1 O_2) и (MN) — диагонали в параллелограмме, то есть они точкой пересечения делятся пополам. Значит (O_1 K=KO_2=frac O_1 O_2=10).
3) Проведем из центров окружностей четвре радиуса к сторонам прямоугольника в точки касания, получились два четырехугольника: (VO_1 TA) и (O_2 SDL). (∠O_1 VA=∠ATO_1=∠VAT=90^°) и (VO_1=O_1 T) (как радиусы), следовательно, (VO_1 TA) квадрат. Аналогично доказывается, что (O_2 SDL) квадрат, причем (VO_1 TA=O_2 SDL), так как стороны их равны радиусам.
4) (O_1 O_2 LT) – прямоугольник: (O_1 T=O_2 L) (радиусы) и (∠O_1 TL=∠O_2 LT=90^°), следовательно, (O_1 T∥O_2 L). Значит (TL=O_1 O_2=20).
6) Рассмотрим (∆O_2 KN) – прямоугольный.
(KN=sqrt =sqrt =6).
(MK=KN), т.к. (K) – точка пересечения диагоналей.
(MN=2KN=12).
7) (∆O_1 MN=∆O_2 MN) (т.к. (O_1 MO_2 N) – параллелограмм), следовательно, (S_ =S_ ), а значит (S_ =2S_ ).
(∆O_1 MN) – прямоугольный ((∠O_1 MN=90^°)), значит (S_ =frac MNcdot MO_1=frac cdot 12cdot 8=48).
(S_ =2S_ =96).
Видео:Четыре окружности в параллелограмме | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

В параллелограмме лежат две окружности
В параллелограмме ABCD расположены две равные непересекающиеся окружности. Первая касается сторон AD, AB и BC, вторая — сторон AD, CD и BC.
а) Докажите, что общая внутренняя касательная l окружностей проходит через точку пересечения диагоналей параллелограмма ABCD.
б) Пусть ABCD — прямоугольник, а прямая l касается окружностей в точках M и N. Найдите площадь четырёхугольника с вершинами в точках M, N и в центрах окружностей, если AD = 36 , а расстояние между центрами окружностей равно 20.
а) Пусть O — точка пересечения диагонали AC параллелограмма с общей внутренней касательной l к данным окружностям, P и Q — точки пересечения прямой l со сторонами AD и BC соответственно. Достаточно доказать, что O — середина диагонали AC.
Пусть O1 и O2 — центры первой и второй окружностей соответственно. Первая окружность касается стороны AD в точке K, вторая окружность касается стороны BC в точке L.
Лучи AO1 и CO2 — биссектрисы равных углов BAD и BCD, значит, прямоугольные треугольники AKO1 и CLO2 равны по катету (радиусы равных окружностей) и противолежащему острому углу. Тогда AK = CL. Аналогично KP = LQ. Следовательно,
Значит, треугольники AOP и COQ равны по стороне и двум прилежащим к ней углам, поэтому AO = OC, а точка O — середина диагонали AC, то есть центр параллелограмма ABCD.
б) Поскольку ABCD — прямоугольник, его сторона AD равна сумме диаметра окружности и отрезка O1O2, то есть 2r + O1O2 = AD, 2r + 20 = 36, следовательно, r = 8.
Четырёхугольник O1MO2N — параллелограмм, так как его противоположные стороны O1M и O2N равны и параллельны. Диагонали O1O2 и MN параллелограмма O1MO2N пересекаются в точке O и делятся этой точкой пополам.
Площадь параллелограмма O1MO2N в четыре раза больше площади треугольника OO1M, в котором По теореме Пифагора
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, 🎦 Видео8 класс, 4 урок, ПараллелограммСкачать  Две касающиеся внешним образом в точке А окружности, радиусы которых равны 4 и 8Скачать  ЕГЭ Задание 16 Две окружностиСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Геометрия Две окружности имеют общий центр O (см. рис.). В одной из окружностей проведен диаметр ABСкачать  ОГЭ № 25. "Окружности касаются внешним образом... "Скачать  Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать  Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать  Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать  №8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать  КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать  |










