Все хорды окружности находятся на равном расстоянии от центра окружности

Выясним, какими свойствами обладают равные хорды и равные дуги.

Равные хорды равноудалены от центра окружности.

Дано : окр. (O;R), AB и CD — хорды,

Соединим центр окружности с концами хорд.

I. Рассмотрим треугольники AOB и COD.

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.

II. Рассмотрим прямоугольные треугольники AOF и COK.

2) ∠A=∠C (по доказанному).

Из равенства треугольников следует равенство соответствующих сторон: OF=OK.

Что и требовалось доказать .

Если хорды равноудалены от центра окружности, то они равны.

Дано: окр. (O;R), AB и CD — хорды,

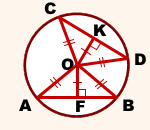
Соединим центр окружности с концами хорд.

I. Рассмотрим прямоугольные треугольники OKD и OFB.

1)OF=OK (по условию)

2)OD=OB (как радиусы).

Из равенства треугольников следует равенство соответствующих сторон:

II. Рассмотрим треугольники AOB и COD.

Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.

По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.

Что и требовалось доказать.

Равные хорды стягивают равные дуги.

Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.

Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD

Что и требовалось доказать .

Хорды, стягивающие равны дуги, равны.

Дано: окр. (O;R), AB и CD — хорды,

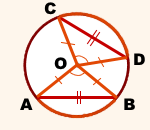
Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.

Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.

Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Докажите, что хорды, удалённые от центра окружности на равные расстояния, равны.

Если данные хорды проходят через центр окружности, то утверждение очевидно.

Пусть AB и A₁B₁ — хорды окружности с центром O, удалённые на одинаковые положительные расстояния от точки O. Расстояния от центра окружности до этих хорд равны перпендикулярам OM и OM₁, опущенным на хорды из центра окружности. Высоты OM и OM₁ равнобедренных треугольников AOB и A₁OB₁ являются их медианами, поэтому точки M и M₁ — середины хорд. Прямоугольные треугольники AMO и A₁M₁O равны по катету и гипотенузе (радиус окружности). Поэтому AM = AM₁. Следовательно, AB = A₁B₁.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Свойства хорд

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

свойства хорды в окружности

Свойство 1
1. Диаметр окружности CD, перпендикулярный хорде AB, делит хорду пополам, и наоборот: CD ? AB AF = FB .

Свойство 2
2. Равные хорды хорды находятся на равном расстоянии от центра окружности: AB = CD ? OE = OF .

Свойство 3
3. Дуги окружности, заключенные между параллельными хордами, равны между собой: AB || CD ? ? AC = ? BD .

Свойство 4
4. Если хорды AB и CD окружности пересекаются в точке S, то AS • SB = CS • SD .

Свойство 5
5. Если хорда AB проходит через внутреннюю точку M круга радиуса R и расстояние до M от центра OM = d , то AM • MB = R 2 — d 2 .

🌟 Видео

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

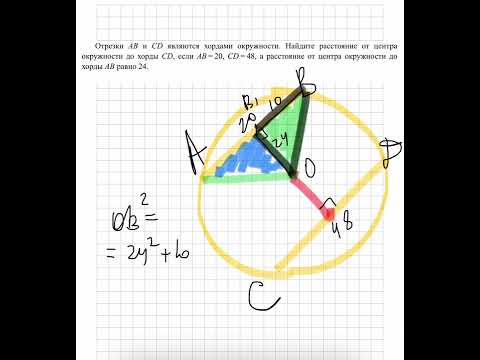
Окружность, диаметр, хорда геометрия 7 классСкачать

Геометрия Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Радиус и диаметрСкачать

ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ХОРДЫ В ОКРУЖНОСТИСкачать

Радиус Хорда ДиаметрСкачать

Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Окружность. 7 класс.Скачать

Окружность и круг, 6 классСкачать

Найти центр и радиус окружностиСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать