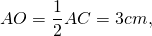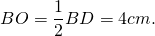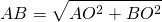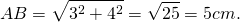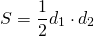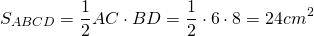Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.
Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
- Площадь параллелограмма по основанию и высоте параллелограмма
- Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
- Площадь параллелограмма по двум сторонам и углу между ними
- Площадь параллелограмма по двум диагоналям и углу между этими диагоналями
- Площадь параллелограмма по вписанной окружности и стороне
- Площадь параллелограмма по вписанной окружности и углу между сторонами
- Таблица с формулами площади параллелограмма
- Определения
- В параллелограмм вписана окружность найти площадь
- В параллелограмм вписана окружность
- 🌟 Видео
Видео:Задание 24 ОГЭ по математике #5Скачать
Площадь параллелограмма по основанию и высоте параллелограмма
Видео:Сможешь найти площадь параллелограмма? Внутри него есть две окружностиСкачать

Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
Видео:Когда в параллелограмм можно вписать окружность. 15 задание ОГЭСкачать

Площадь параллелограмма по двум сторонам и углу между ними
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Площадь параллелограмма по двум диагоналям и углу между этими диагоналями
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Площадь параллелограмма по вписанной окружности и стороне
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
Видео:17 задание ЕГЭ математика профильСкачать

Площадь параллелограмма по вписанной окружности и углу между сторонами
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Видео:В параллелограмме ABCD проведена диагональ AC. Найдите площадь параллелограмма ABCDСкачать

Таблица с формулами площади параллелограмма
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | основание и высота | 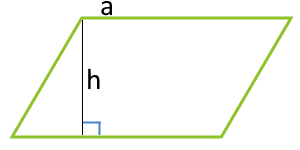 |
| 2 | сторона и высота, опущенная на эту сторону | 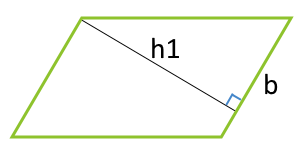 |
| 3 | две стороны и угол между ними | 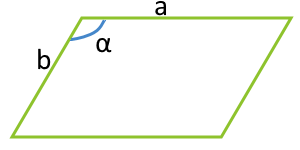 |
| 4 | диагонали и угол между ними | 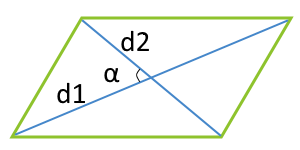 |
| 5 | вписанная окружность и сторона | 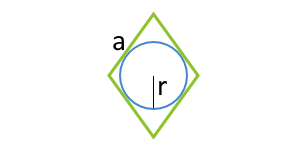 |
| 6 | вписанная окружность и угол между сторонами | 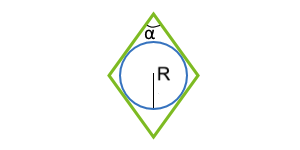 |
Определения
Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.
Некоторые свойства параллелограмма:
- Сумма углов параллелограмма равна 360 градусов
- Сумма углов, прилегающих к любой из сторон равна 180 градусов
- Противоположные стороны параллельны и имеют одинаковую длину
- Противолежащие углы равны
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Видео:Г: В параллелограмм ABCD с углом А, равным 45о, и стороной AD = 10√2 вписана окружность. НайдитеСкачать

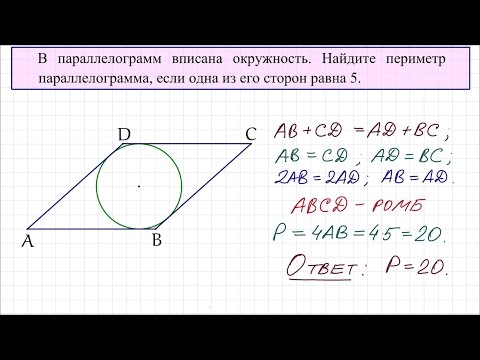
В параллелограмм вписана окружность найти площадь
В параллелограмм вписана окружность.
а) Докажите, что этот параллелограмм — ромб.
б) Окружность, касающаяся стороны ромба, делит её на отрезки, равные 5 и 3. Найдите площадь четырёхугольника с вершинами в точках касания окружности со сторонами ромба.
Пусть это параллелограмм ABCD, а точки касания со сторонами AB, BC, CD, DA обозначены за E, F, G, H соответственно.
а) Из описанности ABCD следует, что AB + CD = AD + BC, то есть 2AB = 2AD, значит, все стороны параллелограмма равны и это ромб.
б) Будем считать, что AE = 3, EB = 5. Центром окружности будет точка пересечения диагоналей ромба O, а радиус этой окружности — высота прямоугольного треугольника Тогда по теореме Пифагора находим
Значит,
Поскольку точки E и F делят стороны AB и BC в одинаковом отношении 3 : 5, треугольники BEF и BAC подобны с коэффициентом и
Рассматривая аналогично остальные стороны EFGH, получаем, что это параллелограмм и даже прямоугольник (так как
). Значит, его площадь равна:
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a и обоснованно получен верный ответ в пункте б | 3 |
| Получен обоснованный ответ в пункте б имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, Видео:8 класс, 13 урок, Площадь параллелограммаСкачать  В параллелограмм вписана окружностьЕсли в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме? Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны. Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба). Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат. Радиус вписанной в ромб окружности можно найти по формуле где S — площадь ромба, p — его полупериметр; или как половину высоты ромба 1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см. Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны. 2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см. Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты: 3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.
Пусть ABCD — ромб, AC=6 см, BD=8 см. Рассмотрим треугольник AOB. По теореме Пифагора полупериметр — p=2a=2∙AB=25=10 см. Следовательно, радиус вписанной окружности равен 🌟 ВидеоГеометрия Задача ЕГЭ 2019 про параллелограмм и вписанную окружностьСкачать  Четыре окружности в параллелограмме | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать  №696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать  найти сторону четырехугольника, в который вписана окружностьСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Найти площадь! Красивейшая задача из Сингапура!Скачать  Запомни: все формулы для площади треугольникаСкачать  Задача: найти площадь параллелограмма (bezbotvy)Скачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Интересный штрих) параллелограмма ✧ Запомнить за 1 мин!Скачать  Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать  |
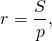
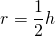
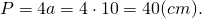
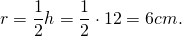
 Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).
Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).