 Школе NET
Школе NET Register
Do you already have an account? Login
Login
Don’t you have an account yet? Register
Newsletter
Submit to our newsletter to receive exclusive stories delivered to you inbox!
- Главная
- Вопросы & Ответы
- Вопрос 9753735
Онтонио Веселко
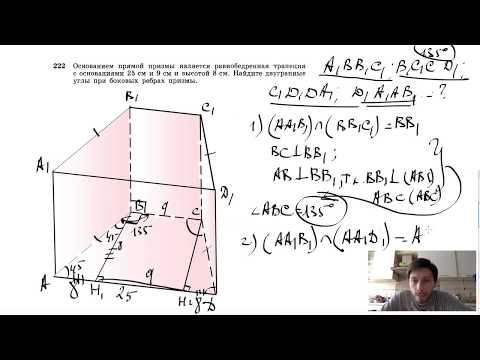
Видео:№222. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 смСкачать
Всем привет 🙂
Господа, прошу вашей помощи по геометрии. Вот, собственно, две задачи:
1) В основании прямой призмы лежит трапеция. Объем призмы равен 40 см . Площади
параллельных боковых граней равны 6 см и 14 см . Найдите расстояние между ними.
2) Диагональ меньшей боковой грани прямоугольного параллелепипеда равна большему
ребру основания. Высота параллелепипеда равна 2 см, диагональ основания равна
14 см. Найдите объем параллелепипеда.
Видео:Найдите площадь поверхности прямой призмы, в основании которой лежит ромб 8 задание ЕГЭ математикаСкачать

Объем цилиндра — урок 3 — КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Самостоятельная работа (20-25 мин.)
1. Основание прямой призмы — прямоугольный треугольник с катетом 6 см и острым углом 45°. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 8√2 см. Найдите объем цилиндра. .
1. Основанием прямой призмы является ромб со стороной 12 см и углом 60°. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 6√2 см. Найдите объем цилиндра.
1. Основанием прямой призмы служит треугольник со сторонами 10, 10 и 12 см. Через большую сторону нижнего основания и середину противоположного бокового ребра проведена плоскость под углом 60° к плоскости основания. Найдите объем призмы.
2. Сечение цилиндра, параллельное его оси, отсекает от окружности основания дугу в 120°. Радиус основания цилиндра равен R, а угол между диагональю сечения и осью цилиндра равен 30°. Найдите объем цилиндра.
1. Основанием прямой призмы АВСА1В1С1 служит треугольник ABC, у которого АВ = ВС = 10, ∠ABC = 30°. Через ребро АА1 проведена плоскость, перпендикулярная грани СС1В1В. Диагональ сечения составляет с плоскостью основания угол в 45°. Найдите объем призмы.
2. Плоскость, параллельная оси цилиндра, проходит от нее на расстоянии 15 см. Диагональ получившегося сечения равна 20 см, а радиус основания цилиндра 17 см. Найдите объем цилиндра.
1. В основании прямой призмы лежит трапеция. Площади параллельных боковых граней призмы равны 8 см2 и 12 см2, а расстояние между ними равно 5 м. Найдите объем призмы.
2. В цилиндр вписана правильная четырехугольная призма, у которой диагональ равна α и образует с боковым ребром угол β. Найдите объем цилиндра.
1. В основании прямой призмы лежит трапеция. Объем призмы равен 40 см3. Площади параллельных боковых граней равны 6 см2 и 14 см2. Найдите расстояние между ними.
2. В цилиндр вписана правильная шестиугольная призма, большая диагональ которой равна l и образует с боковым ребром угол α. Найдите объем цилиндра.
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

В основании прямой призмы лежит трапеция площади параллельных боковых граней 8 и 12
БАЗА ЗАДАНИЙ
Задание № 5. Стереометрия.
1. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
3. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
4. Площадь поверхности куба равна 24. Найдите его объем.
5. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.
6. Площадь поверхности куба равна 8. Найдите его диагональ.
7. Объем куба равен 24√3. Найдите его диагональ.
8. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.
10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
11. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
12. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
13. В основании прямой призмы лежит ромб с диагоналями, равными 9 и 12. Площадь ее поверхности равна 468. Найдите боковое ребро этой призмы.
14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
15. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
18. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
19. Диагональ прямоугольного параллелепипеда равна √8 и образует углы 30°,30° и 45° с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
20. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что BB 1 =32, AB=12, AD=9. Найдите площадь сечения проходящее через вершины A, A 1 , C.
22. Дана правильная четырёхугольная призма ABCDA 1 B 1 C 1 D 1 , площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, B 1 .
23. Найдите объём многогранника, вершинами которого являются точки C, A1 , B1 , C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 4, а боковое ребро равно 9.
24. Найдите объём многогранника, вершинами которого являются точки A, C, A 1 , B1, C 1 правильной треугольной призмы ABCA 1 B 1 C 1 . Площадь основания призмы равна 7, а боковое ребро равно 9.
25. В правильной треугольной призме ABCA 1 B 1 C 1 все ребра равны 3. Найдите угол между прямыми AA1и BC1. Ответ дайте в градусах.
26. В правильной треугольной призме ABCA 1 B 1 C 1 известно, что AB=√3AA 1 . Найдите угол между прямыми AB1 и CC1. Ответ дайте в градусах.
27. Объём куба равен 16. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
29. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 4,5. Найдите объем треугольной пирамиды AD 1 CB 1 .
30. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 1,5. Найдите объем треугольной пирамиды ABCB 1 .
31. Найдите объем параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объем треугольной пирамиды ABDA 1 равен 3.
32. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол 60° и равно 2. Найдите объем параллелепипеда.
33. Найдите объём многогранника ACDFA 1 C 1 D 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 9, а боковое ребро равно 11.
34. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E 1 D 1 .
35. Найдите объём многогранника DA 1 B 1 C 1 D 1 E 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 2.
36. Найдите объём многогранника CDEC 1 D 1 E 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 6, а боковое ребро равно 14.
37. Найдите объём многогранника A 1 B 1 F 1 A правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 15.
38. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
39. В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.
40. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
41. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
42. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.
💥 Видео
КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

8 класс, 15 урок, Площадь трапецииСкачать

Площадь поверхности призмы. 11 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

10 класс, 30 урок, ПризмаСкачать

СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать

Стереометрия №3. Решение всех типов задач | Математика ЕГЭ для 10 класса | УмскулСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

ЕГЭ 2015 Профиль #16 - часть II : В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCDСкачать

Стереометрия с нуля и до уровня ЕГЭ за 4 часа | Вся теория и задачи по №13 | Математика профильСкачать

ЕГЭ стереометрия Сечение призмы Площадь сеченияСкачать



















