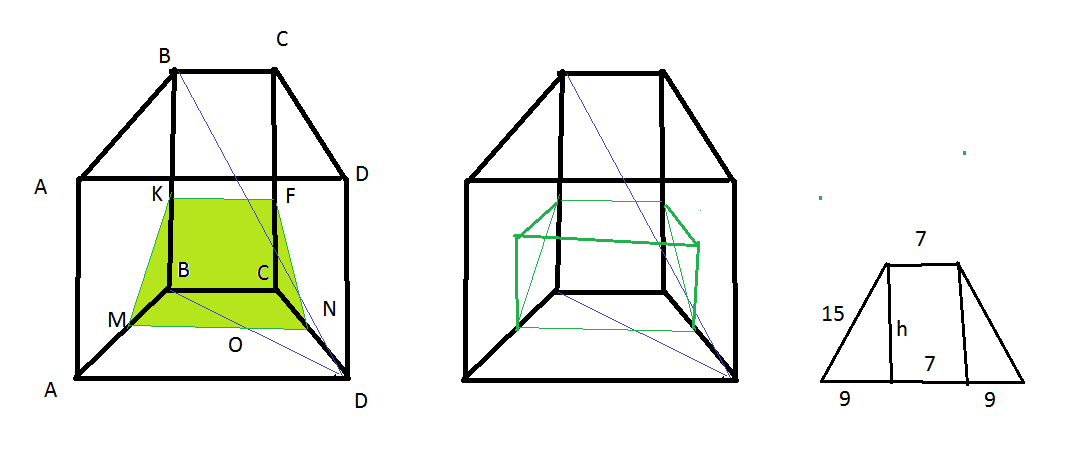
В основании прямой призмы ABCDA1B1C1D1 лежит равнобедренная трапеция ABCD с основаниями ВС и AD. Точка К — середина ребра ВВ1. Плоскость а проходит через середины ребер АВ и ВВ1 параллельно прямой B1D.
А) Докажите, что сечением призмы плоскостью α является равнобедренная трапеция.
Б) Найдите объем большей части призмы, на которые ее разбивает плоскость α, если известно, что ВС=7, AD=25, АВ=15, ВВ1=8.
А) Пусть [math]M[/math] — середина [math]AB[/math]. Тогда [math]alphacap(ABB_1)=MK[/math]
Проведем [math]B_1D;BD;KFparallel B_1D[/math], тогда [math]alphacap(ABC)=MT[/math], где [math]Fin MT[/math]. Точка [math]K[/math]-середина [math]BB_1[/math], [math]KFparallel B_1DRightarrow F[/math] — середина [math]BD[/math] и [math]MF[/math] — средняя линия [math]bigtriangleup ABD[/math][math]Rightarrow MTparallel ADparallel BC[/math]. Тогда [math]MTparallel(BCC_1)[/math] и [math]alphacap(BCC_1)=KLparallel BC[/math].
Имеем [math]KLparallel BCparallel MT;KL=BCneq MTRightarrow MKLT[/math] — трапеция. А так как [math]bigtriangleup MBK=bigtriangleup TCL[/math] по двум катетам, то [math]MK=TL[/math] и [math]MKLT[/math] — равнобедренная трапеция.
Б) [math]V_=S_cdot AA_1[/math], [math]BH[/math] — высота [math]ABCD[/math]; [math]AH=frac2=9[/math], тогда [math]BH=12[/math], [math]S_=frac2cdot12=192;V_=192cdot8=1536[/math]
Плоскость [math]alpha[/math] разбивает призму на две части, меньшая из которых многогранник [math]MBKTCL[/math]. Плоскость [math]MBL[/math] разбивает этот многогранник на две пирамиды [math]LMBCT[/math] и [math]MBKL[/math], объемы которых обозначим [math]V_1[/math] и [math]V_2[/math] соответственно.
[math]V_1=frac13S_cdot CL;CL=4;MBCT[/math] — трапеция, высота которой [math]h=frac2=6;MT=frac2=16[/math], тогда [math]V_1=frac13cdotfrac2cdot6cdot4=92[/math]
[math]V_2=frac13cdot S_cdotrho(M;(BKL));S_=frac12BKcdot BC=frac12cdot7cdot4=14[/math]
[math]M[/math] — середина [math]AB[/math], тогда [math]rho(M,(BKL))=frac2=frac2=6[/math] и [math]V_2=frac13cdot14cdot6=28[/math]
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Задача 11836 .
Условие
В основании прямой призмы АВСDA1B1C1D1 лежит равнобедренная трапеция АВСD с основаниями ВС и АD. Точка К – середина ребра ВВ1. Плоскость α проходит через середины ребер АВ и ВВ1 параллельно прямой В1D.
А) Докажите, что сечением призмы плоскостью α является равнобедренная трапеция.
Б) Найдите объем большей части призмы, на которые ее разбивает плоскость α, если известно, что ВС=7, АD=25, АВ=15, ВВ1=8.
Решение
Пусть М- середина АВ, АМ=МВ.
В треугольнике ВВ1D проводим КО || B1D.
Так как ВК=КВ1, КО- средняя линия треугольника ВВ1D.
BO=OD.
МО — средняя линия треугольника АВD,
MO||AD, AD||BC, значит МО||ВС.
MN-средняя линия трапеции АВСD.
CN=ND.
КF||BC, KF=BC,
C1F=FC.
KF||MN, значит ABCD- трапеция.
Грани AA1B1B и СС1D1D- равны. AA1=BB1=CC1=DD1.
AB=CD.
Значит и диагонали этих граней равны. АВ1=DC1
MK=AB1/2=DC1/2=FN
Cечение МКFN — равнобедренная трапеция.
Б) h(трапеции)=sqrt(15^2-9^2)=12
MN=(BC+AD)/2=(7+25)/2=16
V(призмы АВСВА1В1С1D1)=S(трапеции АВСD)*H=
=((7+25)*12/2)*8=1536 куб.ед.
v(меньшей части)=1/2 V1
V1-объем прямой призмы с основанием МВСN и высотой КВ=Н/2.
V1=((BC+MN)*h/2)/2(*H/2)=((7+16)*6/2)*4=276
v=276/2=138 куб.ед.
V(большей части)=V(призмы АВСВА1В1С1D1)-v(меньшей части)=1536-138=1398 куб.ед
О т в е т. 1398 куб. ед.
Видео:№222. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 смСкачать
Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Видео:№599. Найдите площадь равнобедренной трапеции с основаниями 2 см и 6 см, если уголСкачать

Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Видео:Урок 35. Равнобедренная и прямоугольная трапеции (8 класс)Скачать

Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
💥 Видео
№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

8 класс, 6 урок, ТрапецияСкачать

Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать

13_1 ЕГЭ 2023Скачать

№799. Дана равнобедренная трапеция ABCD. Перпендикуляр, проведенный из вершины В к большему основаниСкачать

Высота равнобедренной трапеции, проведённая ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

№24. Точка М не лежит в плоскости трапеции ABCD с основанием AD.Скачать

ЕГЭ Задание 16 Равнобедренная трапеция Вписанные окружностиСкачать

ЕГЭ 2023, математика профиль, 13 заданияСкачать
№438. В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CDСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать