В основании правильной пирамиды может быть только четырехугольника

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Зачёт №2 «Многогранники».

К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

Какие из утверждений справедливы для правильной пирамиды:

— в её основании лежит правильный многоугольник;

— все её грани правильные многоугольники;

— АПОФЕМОЙ называется высота правильной пирамиды;

— отрезок, соединяющий вершину пирамиды с центром основания, является её высотой;

— все боковые грани правильной пирамиды равны;

— основанием правильной пирамиды может быть квадрат;

— основанием правильной пирамиды может быть трапеция;

Изображённый на рисунке 2 многогранник называется…………………

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

……………………………………………… . равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

6. Практическая работа

Найдите площадь полной поверхности прямоугольного параллелепипеда (коробки) №…….

Зачёт №2 «Многогранники».

К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

Какие из утверждений справедливы для правильной пирамиды:

— в её основании может лежать любой многоугольник;

— все её боковые грани равнобедренные треугольники;

— высота её боковой грани, проведённая из вершины, называется АПОФЕМОЙ;

— высота правильной пирамиды не всегда совпадает с центром основания;

— все ребра правильной пирамиды равны;

— основанием правильной пирамиды может быть ромб;

— основанием правильной пирамиды может быть равносторонний треугольник;

Изображённый на рисунке 2 многогранник называется…………………

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

5.О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

……………………………………………… . равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

Найдите площадь полной поверхности прямоугольного параллелепипеда (коробки) № …..

Зачёт №2 «Многогранники».

К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

Какие из утверждений справедливы для правильной пирамиды:

— в её основании может лежать равносторонний треугольник;

— все её боковые грани равны;

— АПОФЕМОЙ называется боковое ребро правильной пирамиды;

— высота правильной пирамиды всегда совпадает с центром основания;

— все грани правильной пирамиды равны;

— основанием правильной пирамиды может быть прямоугольник;

— основанием правильной пирамиды может быть равнобедренный треугольник;

Изображённый на рисунке 2 многогранник называется………………….

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

5.О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

……………………………………………… . равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

Найдите площадь полной поверхности прямоугольного параллелепипеда (коробки) № ….

Зачёт №2 «Многогранники».

К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

Какие из утверждений справедливы для правильной пирамиды:

— в её основанием может быть только четырехугольник;

— все её боковые ребра равны;

-медиана её боковой грани, проведённая из вершины, является АПОФЕМОЙ;

— отрезок, соединяющий вершину пирамиды с центром окружности, описанной около основания этой пирамиды, является её высотой;

— все боковые грани правильной пирамиды имеют равные площади;

— основанием правильной пирамиды может быть прямоугольный треугольник;

— основанием правильной пирамиды может быть параллелограмм;

Изображённый на рисунке 2 многогранник называется…………………

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

5.О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

……………………………………………… . равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

Найдите площадь полной поверхности прямоугольного параллелепипеда (коробки) № …..

Видео:В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 690 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Кабулова Сауле ЖакановнаНаписать 10441 13.01.2016

Номер материала: ДВ-334996

13.01.2016 1373

13.01.2016 481

13.01.2016 368

13.01.2016 1499

13.01.2016 900

13.01.2016 676

13.01.2016 834

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Что такое правильная пирамида: определение, виды, свойства

В данной публикации мы рассмотрим определение, виды (треугольная, четырехугольная, шестиугольная) и основные свойства правильной пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Определение правильной пирамиды

Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

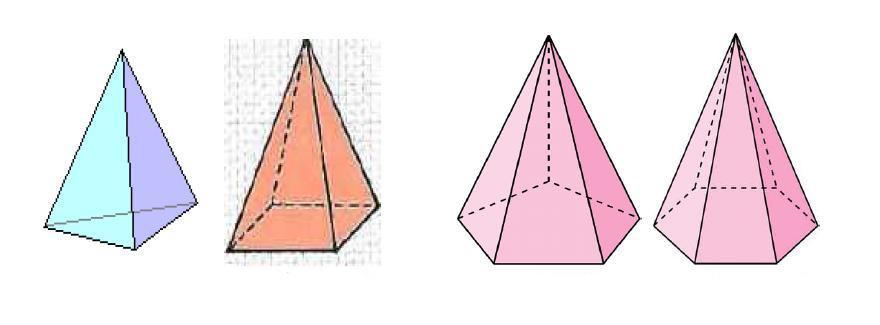
Самые распространенные разновидности правильных пирамид: треугольная, четырехугольная и шестиугольная. Рассмотрим их подробнее.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Виды правильной пирамиды

Правильная треугольная пирамида

• Основание – правильный/равносторонний треугольник ABC.
• Боковые грани – одинаковые равнобедренные треугольники: ADC, BDC и ADB.

Примечание: если у правильной треугольной пирамиды все ребра равны, она также называется правильным тетраэдром.

Правильная четырехугольная пирамида

• Основание – правильный четырехугольник ABCD, другими словами, квадрат.
• Боковые грани – равные равнобедренные треугольники: AEB, BEC, CED и AED.
• Проекция вершины E на основание – точка O, является точкой пересечения диагоналей квадрата ABCD.
• EO – высота фигуры.
• EN и EM – апофемы (всего их 4, на рисунке в качестве примера изображено только два).

Правильная шестиугольная пирамида

• Основание – правильный шестиугольник ABCDEF.
• Боковые грани – равные равнобедренные треугольники: AGB, BGC, CGD, DGE, EGF и FGA.
• Проекция вершины G на основание – точка O, является точкой пересечения диагоналей/биссектрис шестиугольника ABCDEF.
• GO – высота пирамиды.
• GN – апофема (всего их должно быть шесть).

Видео:Построение сечения пирамиды по трем точкамСкачать

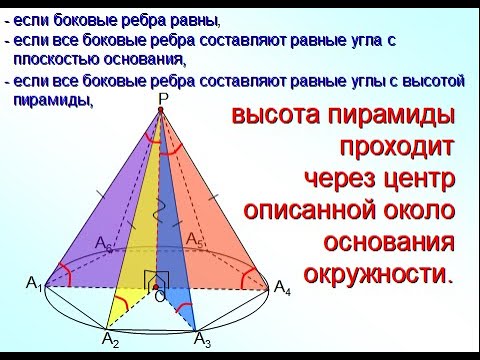
Свойства правильной пирамиды

1. Все боковые ребра фигуры равны. Другими словами вершина пирамиды находится на одинаковом расстоянии от всех углов ее основания.
2. Угол между всеми боковыми ребрами и основанием одинаковый.
3. Все грани наклонены к основанию под одним и тем же углом.
4. Площади всех боковых граней равны.
5. Все апофемы равны.
6. Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения перпендикуляров, проведенных к серединам боковых ребер.

Примечание: Формулы для нахождения площади поверхности, а также объема пирамиды представлены в отдельных публикациях.

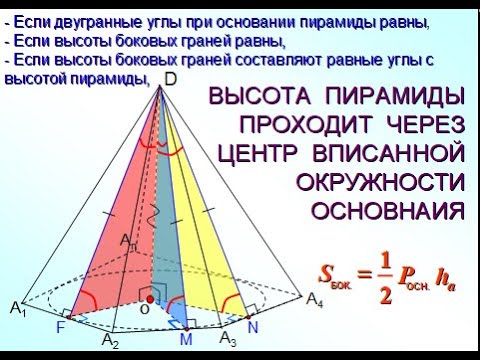
Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .

Видео:Геометрия 10 класс (Урок№15 - Пирамида.)Скачать

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

• в основании должен находиться правильный многоугольник;
• боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:Правильная пирамида № 258Скачать

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Видео:Трапеция, решение задач. Вебинар | МатематикаСкачать

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Видео:№269. Стороны оснований правильной треугольной усеченной пирамиды равны 4 дм и 2 дм, а боковое реброСкачать

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

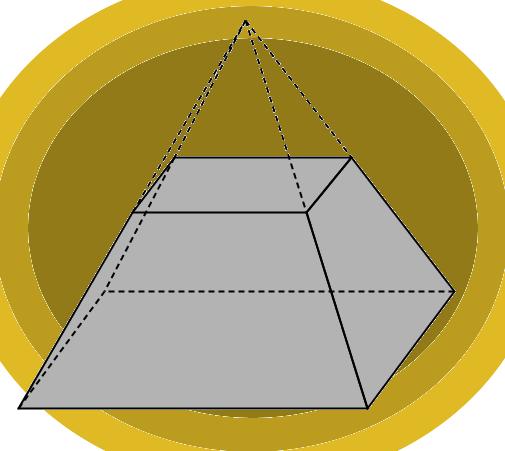
Свойства правильной усеченной четырехугольной пирамиды

Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Здесь h — расстояние между основаниями фигуры, So1, So2 — площади нижнего и верхнего оснований.

🎥 Видео

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать

Развертка пирамидыСкачать

А что, если пирамиды построили для... (Продолжение)Скачать

Делаем модель пирамиды для решения задачи по стереометрииСкачать

10 класс — Разбор задач по теме "Пирамида"Скачать

С2 по математике, ЕГЭ 2014, диагностическая 2 (12.12). Правильная четырехугольная пирамидаСкачать

Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать