В ортогональных проекциях сохраняется аффинное соответствие эллипса окружности которое формулируется

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Что за зверь — аффинные преобразования?

Скорее всего, каждый из Вас хоть раз в жизни слышал термин «аффинные преобразования». Действительно, все постоянно о них говорят: «инвариантность к аффинным преобразованиям», «аугментация с помощью аффинных преобразований», «аффинные преобразования в компьютерной графике» и так далее. Однако, далеко не все могут сходу ответить на простой вопрос: «А расскажите, что такое аффинные преобразования простыми словами».

Вы сможете? В любом случае, давайте немного обсудим этот вопрос.

Видео:Аффинная геометрияСкачать

Что такое аффинное преобразование?

Начнем с классики — определение из Википедии.

Аффинное преобразование (от лат. affinis «соприкасающийся, близкий, смежный») — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.

Внесем немного ясности.

Во-первых, что значит «отображение в себя»? Это значит, что если мы находились в пространстве , то после образования мы должны остаться в нем же. Например: если мы применили какое-то преобразование к прямоугольнику и получили параллелепипед, то мы вышли из в . А вот если из прямоугольника у нас получился другой прямоугольник, то все хорошо, мы отобразили исходное пространство в себя. Формально это описывается так: «преобразование отображает пространство в ». Если записать с помощью формул: .

Во-вторых, что такое «скрещивающиеся прямые»? Конечно, все это проходили в школе, но на всякий случай напомним. Прямые называются скрещивающимися, если они не лежат в одной плоскости. Вот если бы они лежали в одной плоскости и пересекались, они назывались бы пересекающимися. А если в разных плоскостях, то скрещивающимися. Пример — на рисунке.

В целом, это определение уже нам что-то говорит и мы начинаем потихоньку рисовать для себя картинку. Как минимум, мы должны остаться в той же плоскости: значит мы представляем себе декартову систему координат. Здесь речь идет о нескольких прямых, так что давайте представим 2 параллельных линии. Из определения мы понимаем, что после преобразования эти линии должны остаться параллельными. Ну что ж, тогда просто сдвигаем их куда-нибудь из исходного местоположения, да и все.

По сути, мы с Вами только что описали один из видов аффинных преобразований — сдвиг.

Но давайте пойдем чуть дальше и дадим еще одно определение (не нами придуманное).

Преобразование плоскости называется аффинным, если оно непрерывно, взаимно однозначно и образом любой прямой является прямая.

Звучит это, пожалуй, чуть сложней и путанней, но дает нам больше конкретной информации, чем предыдущее определение.

Преобразование называется непрерывным, если «близкие точки переходят в близкие». Т.е. иначе — если у нас есть две точки и они находятся рядом, то после преобразования они все равно будут находиться где-то поблизости друг от друга.

Далее — преобразование взаимооднозначно, если разные точки переводятся в разные точки и в каждую точку переводится какая-то точка. Например: если мы отобразили отрезок и он слипся в точку — это не взаимооднозначное преобразование. Из отрезка мы должны получить ровно такой же отрезок, тогда будет взаимооднозначно (если это сработает для всех отрезков, конечно).

Итак, с определениями мы разобрались. Давайте теперь запишем в общем виде, а как выглядит преобразование координат в формульном виде.

Пусть у нас есть исходная система координат. Точка в этой системе характеризуется двумя числами — и . Совершить переход к новым координатам и мы можем с помощью следующей системы:

При этом, числа должны образовывать невырожденную матрицу:

На всякий случай: матрица называется невырожденной, если ее определитель не равен нулю, т.е.

Можно записать и в более общем в виде.

Аффинное преобразование — преобразование вида , где — обратимая матрица, а . В данном случае, само собой, -мерный вектор.

Видео:Ортогональная проекция и ортогональная составляющая. ТемаСкачать

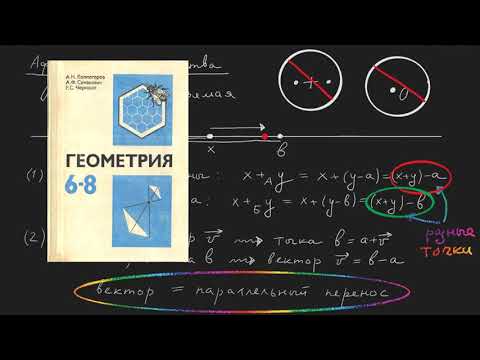
Примеры аффинных преобразований

Мы с Вами достаточно подробно разобрали, что такое аффинное преобразование и как его можно описать с помощью формул. Давайте теперь рассмотрим популярные примеры.

Приходят ли Вам в голову какие-нибудь претенденты на роль? Позвольте мы внесем свои предложения.

Поворот

Пусть .

Значит, матрица примет вид:

И новые координаты будут выглядеть так:

Ничего не напоминает? Если Вы еще не узнали, то встречайте — это просто повернутая система координат на угол . Т.е. мы применили аффинное преобразование и наша система координат повернулась. Пример этого Вы можете видеть на графике.

Растяжение-сжатие

Теперь мы предлагаем сконструировать матрицу несколько иначе:

Новые координаты тогда принимают вид:

В целом, тут даже уже из вида системы уравнений понятно, что мы просто растягиваем наши оси, если коэффициент меньше 1 и сжимаем, если больше 1. Пример на рисунке.

Кстати говоря, а попробуйте поставить вместо число -1, а вместо просто 1. Что получится? Правильно, мы просто отразим нашу систему координат относительно оси .

Сдвиг

Ну и давайте напоследок еще один пример.

Пусть теперь матрица никак не меняет исходные координаты (т.е. ). А вот пусть равняется , а .

Таким образом, наша система принимает вид:

Если отразить это на графике, то мы просто сдвинули начало координат в точку . Вот, собственно, и вся премудрость.

Видео:Эллипс - Инженерная графика.Скачать

Эпилог

Эта короткая статья позволит Вам чуть сильней прочувствовать «внутренности» аффинных преобразований (мы надеемся на это). После прочтения попробуйте все-таки ответить на вопрос, который мы ставили в самом начале — «А расскажите, что такое аффинные преобразования простыми словами». Теперь сможете?

P.S. Кстати говоря, было бы неплохо не верить нам на слово и проверить самим — а матрицы , которые мы использовали — точно невырожденные? Может мы вообще что-то противозаконное сделали.

Видео:Геометрия и группы. Алексей Савватеев. Лекция 10.3. Аффинное пространствоСкачать

Аффинные преобразования

Видео:ВСЯ ПРАВДА ПРО АФФИННОЕ ПРЕОБРАЗОВАНИЕСкачать

Образ прямой линии.

Изучим геометрические свойства аффинных преобразований. Ниже (f) обозначает аффинное преобразование, записываемое в декартовой системе координат (O, boldsymbol_, boldsymbol_) формулами
$$
x^=a_x+b_y+c_, y^=a_x+b_y+c_.label
$$
при условии
$$
begin
a_& b_\
a_& b_
end neq 0.label
$$

Более того, преобразование (f) определяет взаимно однозначное отображение одной прямой на другую, так как при сделанном здесь выборе начальных точек и направляющих векторов точка (M^) имеет на прямой eqref то же значение параметра (t), что и точка (M) на исходной прямой. Отсюда мы получаем первое утверждение.

При аффинном преобразовании:

• прямая линия переходит в прямую линию;
• отрезок переходит в отрезок;
• параллельные прямые переходят в параллельные.

Для доказательства второго утверждения достаточно заметить, что отрезок прямой состоит из таких точек, у которых значения параметра удовлетворяют неравенству вида (t_ leq t leq t_) Третье утверждение следует из того, что при аффинном преобразовании коллинеар-ные векторы переходят в коллинеарные.

При аффинном преобразовании отношение длин параллельных отрезков не изменяется.

Пусть отрезки (AB) и (CD) параллельны. Это значит, что существует такое число (lambda), что (overrightarrow=lambda overrightarrow). Образы векторов (overrightarrow) и (overrightarrow) связаны той же зависимостью (overrightarrow<A^B^>=lambda overrightarrow<C^D^>). Отсюда вытекает, что
$$
frac<|overrightarrow|><|overrightarrow|>=frac<|overrightarrow<A^B^>|><|overrightarrow<C^D^>|>=|lambda|.nonumber
$$

Если точка (C) делит отрезок (AB) в некотором отношении (lambda), то ее образ (C^) делит образ (A^B^) отрезка (AB) в том же отношении (lambda).

Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Изменение площадей при аффинном преобразовании.

Для начала рассмотрим ориентированный параллелограмм. Выберем общую декартову систему координат (O, boldsymbol_, boldsymbol_) и обозначим через ((p_, p_)) и ((q_, q_)) компоненты векторов (boldsymbol

) и (boldsymbol), на которых он построен. Площадь параллелограмма мы можем вычислить, пользуясь формулой:
$$
S_=S_ (boldsymbol

, boldsymbol)=(p_q_-p_q_) S_ (boldsymbol_, boldsymbol_).nonumber
$$

Пусть аффинное преобразование (f) записывается в выбранной системе координат формулами eqref. Из ранее доказанного утверждения следует, что векторы (f(boldsymbol

)) и (f(boldsymbol)) имеют в базисе (f(boldsymbol_), f(boldsymbol_)) те же компоненты ((p_, p_)) и ((q_, q_)), что и векторы (boldsymbol

) и (boldsymbol) в базисе (boldsymbol_, boldsymbol_). Образ параллелограмма построен на векторах (f(boldsymbol

)) и (f(boldsymbol)), и площадь его равна
$$
S_^=S_ (f(boldsymbol

), f(boldsymbol))=(p_q_-p_q_) S_ (f(boldsymbol_), f(boldsymbol_)).nonumber
$$

Вычислим последний множитель. Как мы знаем из уже доказанного утверждения 7, координаты векторов (f(boldsymbol_), f(boldsymbol_)) равны соответственно ((a_, a_)) и ((b_, b_)). Поэтому (S_ (f(boldsymbol_), f(boldsymbol_))=(a_b_-a_b_) S_ (boldsymbol_, boldsymbol_)) и
$$
S_^=(p_q_-p_q_)(a_b_-a_b_) S_ (boldsymbol_, boldsymbol_).nonumber
$$
Отсюда мы видим, что
$$
frac<S_^><S_>=begin
a_& b_\
a_& b_
end.label
$$

Таким образом, отношение площади образа ориентированного параллелограмма к площади этого параллелограмма одинаково для всех параллелограммов и равно (a_b_-a_b_).

Отсюда следует, что данный детерминант не зависит от выбора системы координат, в которой записано преобразование, хотя он вычисляется по коэффициентам, зависящим от системы координат. Эта величина — инвариант, выражающий геометрическое свойство преобразования.

Из формулы eqref видно, что отношение площади образа неориентированного параллелограмма к его площади равно
$$
S^/S=|a_b_-a_b_|.label
$$

Если (a_b_-a_b_ > 0), то ориентации всех ориентированных параллелограммов сохраняются при преобразовании, а если (a_b_-a_b_ Утверждение 3.

Аффинное преобразование переводит алгебраическую линию в алгебраическую линию того же порядка.

В самом деле, пусть линия (L) в декартовой системе координат (O, boldsymbol_, boldsymbol_) имеет алгебраическое уравнение порядка (p). Мы уже доказали, что образы всех точек линии (L) при аффинном преобразовании (f) имеют в системе координат (f(O), f(boldsymbol_), f(boldsymbol_)) те же координаты, что и их прообразы в системе координат (O, boldsymbol_, boldsymbol_). Следовательно, координаты образов в системе (f(O), f(boldsymbol_), f(boldsymbol_)) связаны тем же алгебраическим уравнением порядка (p). Этого достаточно, чтобы сделать нужное нам заключение.

Из доказанного выше утверждения, в частности, следует, что линия второго порядка при аффинном преобразовании перейдет в линию второго порядка. Мы докажем более сильное утверждение. Как мы уже знаем, линии второго порядка можно разделить на семь классов. Мы увидим, что класс линии сохраняется при аффинном преобразовании. На этом основании классы линий, перечисленные в указанной теореме, называются аффинными классами. Итак, докажем новое утверждение.

Линия второго порядка, принадлежащая к одному из аффинных классов, при любом аффинном преобразовании может перейти только в линию того же класса. Каждую линию второго порядка подходящим аффинным преобразованием можно перевести в любую другую линию того же аффинного класса.

Линию мы назовем ограниченной, если она лежит внутри некоторого параллелограмма. Легко видеть, что при аффинном преобразовании ограниченная линия должна перейти в ограниченную, а неограниченная — в неограниченную.

1. Эллипс — ограниченная линия второго порядка. Кроме эллипсов ограничены только линии, состоящие из одной точки, то есть пары мнимых пересекающихся прямых. Поскольку эллипс ограничен и состоит больше, чем из одной точки, он может перейти только в эллипс.
2. Гипербола состоит из двух отдельных ветвей. Это свойство можно сформулировать так, что будет ясна его неизменность при аффинных преобразованиях. Именно, существует прямая линия, не пересекающая гиперболу, но пересекающая некоторые ее хорды.Из всех линий второго порядка только гиперболы и пары параллельных прямых обладают этим свойством. У гиперболы ветви не прямые линии, и потому при аффинном преобразовании она может перейти только в гиперболу.
3. Парабола — неограниченная линия второго порядка, состоящая из одного непрямолинейного куска. Этим свойством не обладают никакие другие линии второго порядка, и потому парабола может перейти только в параболу.
4. Если линия второго порядка представляет собой точку (пару мнимых пересекающихся прямых), прямую (пару совпавших прямых), пару пересекающихся или пару параллельных прямых, то из доказанных ранее свойств аффинных преобразований следует, что эта линия не может перейти в линию никакого другого класса.

Докажем вторую часть предложения. В уже доказанной нами теореме канонические уравнения линий второго порядка написаны в декартовой прямоугольной системе координат и содержат параметры (a, b, …) Если мы откажемся от ортонормированности базиса, то сможем произвести дальнейшие упрощения канонических уравнений и привести их к виду, не содержащему параметров. Например, замена координат (x’=x/a), (y’=y/b) переводит уравнение эллипса (x^a^+y^b^=1) в уравнение (x’^+y’^=1), каковы бы ни были (a) и (b). (Последнее уравнение не есть уравнение окружности, так как новая система координат не декартова прямоугольная.)

Читатель без труда покажет, что канонические уравнения линий второго порядка переходом к подходящей системе координат могут быть преобразованы в уравнения:

Такую систему координат мы назовем аффинной канонической системой координат.

Из ранее доказанного утверждения следует, что аффинное преобразование, которое совмещает аффинные канонические системы координат двух линий одного аффинного класса, совмещает и эти линии. Это заканчивает доказательство.

Видео:#198. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛАСкачать

Разложение ортогонального преобразования.

Каждое ортогональное преобразование раскладывается в произведение параллельного переноса, поворота и, возможно, осевой симметрии.

Пусть (f) — ортогональное преобразование и (vartriangle ABC) — равнобедренный прямоугольный треугольник с прямым углом (A). При преобразовании (f) он перейдет в равный ему треугольник (vartriangle A^B^C^) с прямым углом при вершине (A^). Теорема будет доказана, если, производя последовательно параллельный перенос (p), поворот (q) и (в случае необходимости) осевую симметрию (r), мы сможем совместить треугольники (ABC) и (A^B^C^). Действительно, произведение (rqp) — аффинное преобразование так же, как и (f), а аффинное преобразование однозначно определяется образами трех точек, не лежащих на одной прямой. Поэтому (rqp) совпадает с (f).

Итак, переведем (A) и (A^) параллельным переносом (p) на вектор (overrightarrow<AA^>) (если (A=A^), то (p) — тождественное преобразование). Затем поворотом (q) вокруг точки (A^) совместим (p(B)) с (B^) (возможно, и это преобразование окажется тождественным). Точка (q(p(C))) либо совпадает с (C^), либо симметрична ей относительно прямой (A^B^). В первом случае цель уже достигнута, а во втором потребуется осевая симметрия относительно указанной прямой. Теорема доказана.

Следует иметь в виду, что полученное разложение ортогонального преобразования не однозначно. Более того, можно поворот или параллельный перенос разложить в произведение осевых симметрий, произведение параллельного переноса и поворота представить как один поворот и так далее. Мы не будем уточнять, как это сделать, а выясним следующее общее свойство всех таких разложений.

При любом разложении ортогонального преобразования в произведение любого числа параллельных переносов, поворотов и осевых симметрий четность числа осевых симметрий, входящих в разложение, одна и та же.

Для доказательства рассмотрим на плоскости произвольный базис и проследим за изменением его ориентации (направления кратчайшего поворота от (boldsymbol_) к (boldsymbol_)) при осуществляемых преобразованиях. Заметим, что поворот и параллельный перенос не меняют ориентацию ни одного базиса, а осевая симметрия меняет ориентацию любого базиса. Поэтому, если данное ортогональное преобразование меняет ориентацию базиса, то в любое его разложение должно входить нечетное число осевых симметрий. Если же ориентация базиса не меняется, то число осевых симметрий, входящих в разложение, может быть только четным.

Ортогональные преобразования, которые могут быть разложены в произведение параллельного переноса и поворота, называются ортогональными преобразованиями первого рода, а остальные — ортогональными преобразованиями второго рода.

Ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами:
$$
begin
& x^=x cos varphi mp y sin varphi+c_,\
& y^=x sin varphi pm y cos varphi+c_.
end.nonumber
$$
При верхних знаках коэффициентов у (y) в этих формулах детерминант, составленный из коэффициентов, равен +1, а при нижних знаках он равен —1. Отсюда и из формулы eqref следует следующее утверждение.

Ортогональное преобразование первого рода записывается в декартовой прямоугольной системе координат формулами
$$
begin
& x^=x cos varphi mp y sin varphi+c_,\
& y^=x sin varphi pm y cos varphi+c_.
end.nonumber
$$
с верхними знаками у коэффициентов при (y), а ортогональное преобразование второго рода — с нижними знаками.

Видео:Ортогональные проекции деталиСкачать

Разложение аффинного преобразования.

Мы видели, насколько аффинное преобразование может изменить плоскость: окружность может перейти в эллипс, правильный треугольник — в совершенно произвольный. Казалось бы, никакие углы при этом сохраниться не могут. Однако имеет место следующее утверждение

Для каждого аффинного преобразования существуют две взаимно перпендикулярные прямые, которые переходят во взаимно перпендикулярные прямые.

Для доказательства рассмотрим какую-либо окружность. При данном аффинном преобразовании она перейдет в эллипс. Каждая ось эллипса — множество середин хорд, параллельных другой оси. При аффинном преобразовании хорда перейдет в хорду, параллельность должна сохраниться, а середина отрезка переходит в середину его образа. Поэтому прообразы осей эллипса — отрезки, обладающие тем же свойством: каждый из них есть множество середин хорд окружности, параллельных другому отрезку. Такие отрезки непременно являются двумя взаимно перпендикулярными диаметрами окружности. Это то, что нам требовалось: существуют два взаимно перпендикулярных диаметра окружности, которые переходят во взаимно перпендикулярные отрезки — оси эллипса.

Стоит отметить один особый случай: окружность при аффинном преобразовании может перейти в окружность. В этом случае то же рассуждение проходит с любыми двумя взаимно перпендикулярными диаметрами окружности-образа. Очевидно, что при этом любые два взаимно перпендикулярных направления остаются перпендикулярными.

Два взаимно перпендикулярных направления называются главными или синугулярными направлениями аффинного преобразования (f), если они переходят во взаимно перпендикулярные направления.

Каждое аффинное преобразование раскладывается в произведение ортогонального преобразования и двух сжатий к двум взаимно перпендикулярным прямым.

Доказательство аналогично доказательству теоремы 1. Рассмотрим аффинное преобразование (f) и выберем равнобедренный прямоугольный треугольник (ABC) так, чтобы его катеты (AB) и (AC) были направлены вдоль главных направлений преобразования (f). Обозначим через (A^), (B^) и (C^) образы его вершин. Сделаем такое ортогональное преобразование (g), при котором (g(A)=A^), а точки (g(B)) и (g(C)) лежат соответственно на лучах (A^B^) и (A^C^). (Этого легко добиться, как и в теореме 1, параллельным переносом, поворотом и осевой симметрией.)

Пусть (lambda=|A^B^|/|A^g(B)|), a (mu=|A^C^|/|A^g(C)|). Тогда сжатие (p_) к прямой (A^C^) в отношении (lambda) переведет (g(B)) в (p_g(B)=B^) и не сдвинет точек (A^) и (g(C)). Аналогично, сжатие (p_) к прямой (A^B^) переведет (g(C)) в (p_g(C)=C^) и не сдвинет точек прямой (A^B^).

Это означает, что произведение (p_p_g) переводит точки (A), (B) и (C) в точки (A^), (B^) и (C^) так же, как и заданное нам преобразование (f). Согласно ранее доказанному утверждению имеем (p_p_g=f), как и требовалось.

Видео:A.7.24 Так что же меняет аффинное преобразование?Скачать

Аффинные преобразования на плоскости

IP76 > Аффинные преобразования на плоскости

Аффинные преобразования на плоскости используются в машинной графике повсеместно. Придумал их Эйлер в 18 веке, развил Мёбиус в 19-ом, в 20-м они переместились в графический адаптер и теперь являются неотъемлемой частью нашей с вами жизни…

Аффинное преобразование — это изменение единичной матрицы с учетом матриц масштабирования, перемещения, сдвига и поворота (ниже, в разделе «Ссылки по теме» есть пункт об этих матрицах).

Не смотря на простоту метода, с его применением возникают какие-то сложности, связанные, видимо, с непониманием, почему именно такие матрицы, почему важен порядок, почему это должно работать.

Хотя, как мне кажется, больше отпугивает само понятие матрицы. Давайте рассмотрим, почему матрицы имеют такие коэффициенты и как это все работает.

Видео:Как начертить овал в горизонтальной плоскостиСкачать

Ссылки по теме

Видео:Как начертить овал в профильной плоскостиСкачать

Поворот

Предположим, стоит задача повернуть прямоугольник на некоторый угол относительно его центра. Очевидно, надо рассчитать 4 угловые точки и построить по ним полигон.

Рис.1. Поворот точки Р1 на угол β

Имеем некий прямоугольник с вершинами в точках P1, P2, P3, P4. Рассмотрим точку P1(x,y). Она отстоит от оси абсцисс на угол α. Повернем ее на угол β. Очевидно, что вращение происходит по окружности с центром, находящимся в центре заданного прямоугольника O(x,y).

Рассчитаем координаты новой точки P1′( x′, y′).

Где R – радиус окружности на которой расположена точка P1, и равен (O, P1). Воспользуемся формулами сложения углов (1.1 и 2.1) из справочника:

Рис.2. Координаты точки P1 через угол α

Замечаем, что R × cos(α) это не что иное, как координата X точки P1, а R × sin(α) – координата Y. Таким образом, формулы расчета координат новой точки P1′ приобретают вид:

Чтобы выйти на правильную позицию на холсте, прибавим к полученным значениям координаты центра прямоугольника:

И мы только что получили матрицу поворота аффинного преобразования.

Рис.3. Поворот прямоугольника на угол β относительно его центра

В общем виде формулы можно записать как:

В матричном виде:

Где: M11, M12, M21, M22, Dx, Dy – коэффициенты, определяющие преобразование.

Теперь представим себе, что прямоугольник – это на самом деле бесконечная плоскость. И к каждой точке этой плоскости применены одна и те же формула трансформации. Вот это и будет называться аффинным преобразованием на плоскости.

Таким образом, матрицей поворота будет следующая:

Видео:Лекция №11. Геометрические свойства аффинных преобразованийСкачать

Сдвиг

Еще одно интересное преобразование. Состоит из вертикального сдвига, когда меняется только координата Y, и горизонтального, когда меняется только X.

Для определения величин сдвигов будем использовать углы отклонения от горизонтали или вертикали, т.к. это наиболее часто встречающаяся ситуация.

Снова рассматриваем прямоугольник, помня, что это на самом деле плоскость.

Рис.4. Плоскость с центром трансформации в левой нижней точке P3

Для наглядности деформация будет происходить относительно левой нижней точки P3.

Вначале деформируем следующим образом:

Рис.5. Вертикальный сдвиг

При вертикальном сдвиге координаты X не меняются. Изменяются координаты Y. В данном случае координата Y точки P1 изменилась на расстояние (P2,P2′).

Из чего получим формулу преобразования для Y:

Рис.6. Вертикальный + горизонтальный сдвиги

Теперь добавим горизонтальный сдвиг. Координата X точки P1 изменилась на расстояние (P4,P4′), которое рассчитывается аналогичным образом.

В итоге, формулы для трансформации сдвига выглядят следующим образом:

В позиции M12 находится коэффициент, на который нужно умножить расстояние X, чтобы получить величину вертикального смещения по Y. Аналогично, в позиции М21 находится коэффициент, на который умножается расстояние Y для определения горизонтального сдвига. Это на тот случай, если не нужны углы и заранее знаем, на какие величины хотим деформировать.

Видео:Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Перемещение и масштабирование

Это очень простые матрицы и в свете всего вышесказанного, думаю, понятные и останавливаться на них особого смысла нет. Поэтому, для полноты картины, просто приведу.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Композиция

Давайте сейчас воспринимать композицию, как перемножение матриц в порядке слева направо. На самом деле порядок может быть и обратным — когда матрицы домножаются в начало матричного выражения. Об особенностях порядка перемножения рассказано тут.

Предположим, у нас есть следующее преобразование:

На которое следом идет такое преобразование:

Раскроем скобки и преобразуем:

Это ничто иное, как перемножение матриц коэффициентов:

Соответственно, расчет новых координат выглядит как:

Понятно, что можно умножить получившуюся матрицу на матрицу третьего преобразования, четвертого и т.д. Таким образом, чтобы получить коэффициенты сложного аффинного преобразования, нужно перемножить матрицы коэффициентов в порядке применения трансформаций.

Утверждение, прямо скажем, смелое, но правильное.

Проверим. Допустим, я хочу вначале применить деформацию, а потом повернуть на угол.

Рис.7. Деформация без поворота

На рисунке 7 пока только деформация. Теперь к деформированному прямоугольнику (плоскости) применяю поворот на 80 градусов.

Рис.8. Деформация + поворот

Расчет координат в точности воспроизводит приведенные выше выкладки:

Видео:Усеченный конус: проекции сечения, изометрия и развертка поверхностиСкачать

Применение

Аффинные преобразования изменяют геометрию плоскости, при этом сохраняя параллельность линий и соотношение расстояний.

Безусловно, это один из основных методов обработки изображений. Аффинные преобразования используются для исправления искажений и деформаций, возникающих при не самых идеальных ракурсах камеры. Широко используется в машинном обучении и компьютерном зрении.

Лично мне чаще всего попадались проблемы, которые обобщенно можно выразить двумя вопросами:

Эти два вопроса объединяет одно. Изображение – набор точек, эллипс — геометрическое место точек. Решая вопрос в лоб, надо к каждой точке применить функции поворота. И если для изображения – ну, может быть, то к эллипсу, как фигуре векторной графики, это выглядит топорней некуда.

Аффинное преобразование – это преобразование плоскости. Применяя к плоскости некую трансформацию, мы понимаем, что эта трансформация применяется к каждой точке плоскости. Чтобы плоскость не содержала, это вытянется, сожмется, деформируется, повернется вместе с плоскостью.

Видео:Семинар №12 "Аффинные преобразования плоскости"Скачать

Центр трансформации

Все что мы делали ранее, происходило относительно либо центра прямоугольника, либо одной из его вершин. Это центр трансформации. По сути – это начало координат той координатной системы, в которой происходит трансформация. Поэтому, перед всеми преобразованиями необходимо установить центр системы координат.

В Windows этим занимается функция:

С этой функцией обычно идет еще набор функций, типа изменения окна вывода. Сейчас пока это все не нужно. После применения этой функции начало координат из верхнего левого угла переместиться в указанную точку. Все геометрические построения должны это учитывать. Поэтому лучше изначально писать код так, чтобы все рисовки были в относительных координатах.

Видео:Задание 34 Варианты 4 (5, 6) Группа геометрических телСкачать

Аффинное преобразование Windows

В основе работы с аффинным преобразованием лежит изменение матрицы с учетом масштабирования, перемещения, деформации или поворота. В Windows GDI за матрицу отвечает класс TXForm.

Знакомые обозначения. Поля имеют смысл ровно тот, который описан и в справочнике, и выше в статье. Это коэффициенты матрицы преобразования.

Необходимо проинициализировать поля записи и применить преобразование функцией Windows GDI:

Однако, работать с мировыми координатами и аффинными преобразованиями в Windows GDI — удовольствие так себе. Поэтому рекомендуется это делать в GDI+.

В GDI+ есть масса вариантов, сильно облегчающих жизнь при трансформации плоскости. Но сейчас в плане статьи стоит задача работать именно через матрицы преобразования, поэтому работаем следующим образом.

Необходимо создать экземпляр класса TGPMatrix. Затем проинициализировать его методом:

Снова знакомые имена аргументов. Аргументы имеют тот же смысл, что и поля записи TXForm.

После инициализации применяем трансформацию методом TGPGraphics:

После этих манипуляций рисуем все, что хотим нарисовать, не заботясь о расчетах, углах и синусах.

Представим, что один человек рисует портрет, а второй стоит сбоку и смотрит на холст. Для него портрет выглядит деформированным, а для художника, который смотрит прямо, портрет вполне себе правильный, не трансформированный и пока нравится. Что-то похожее происходит при аффинных преобразованиях. Правда, в приведенном примере трансформация перспективная. Но сути дела это не меняет.

Рекомендован следующий порядок при работе с аффинными преобразованиями:

1. Назначение нового центра координат (спорное утверждение)
2. Инициализация матрицы преобразования
3. Применение матрицы
4. Рисуем эллипс

Видео:Координаты, аффинные преобразования.Скачать

Композиция

Как выше говорилось, при сложном преобразовании, состоящим из нескольких трансформаций, необходимо перемножить матрицы в порядке применения преобразований. За это отвечает функция Windows GDI:

Здесь p2 и p3 — первая и вторая структуры TXForm, результат их комбинирования будет находиться в параметре p1. Т.е. надо понимать, что p3 – это преобразование, накладываемое на p2, т.е. идущее следом за ним. Порядок применения матриц очень важен.

Видео:ОртогональностьСкачать

Практика

Весь исходный код можно скачать по ссылке ниже. Чтобы не загромождать буду фрагментировать. Если приводить весь код в статье, до конца можно никогда не добраться.

Перед вызовом этой функции точка начала координат уже установлена в центр прямоугольника.

Аффинный поворот

Итак, у нас есть демонстрационной приложение, написанное для статьи. Внизу есть ряд кнопок 1..15. Это разные режимы демонстрации. Режимы 9..11 отвечают за демонстрацию аффинных преобразований с предварительным назначением нового центра координат . В режиме 9 видим такую картину:

Рис.9. «Спокойное» аффинное преобразование

Ну, это мы уже видели. Однако, если повернуть прямоугольник, за вершину P1 или в поле «Rotate Angle» увидим интересное изменение:

Рис.10. Подписи к вершинам тоже под углом

Помимо поворота непосредственно прямоугольника, повернулись и подписи вершин.

Преобразование применятся к плоскости, к каждой точке плоскости. Грубо говоря, преобразование применяется ко всему, что на плоскости.

Поэтому, можно предположить, что такой же фокус пройдет и с эллипсом:

Рис.11. Эллипс под углом

То же самое касается и изображения:

Рис.12. Изображение под углом

В чем, собственно, прелесть аффинных преобразований и состоит. Не надо считать каждую точку, писать километры кода. Мы просто рисуем, как будто и нет никаких преобразований, все также прямоугольно, параллельно и перпендикулярно. Все расчеты берет на себя плоскость, к которой применили преобразование.

Фрагмент из вышеприведенного кода:

В функции DrawEllipse нет ничего особенного, вынесена, чтобы не загромождать код:

Т.е. не взирая на все требуемые повороты, деформации и прочие издевательства, спокойно рисуем все в том же прямоугольнике val, все теми же обычными методами.

Аффинный сдвиг

Аналогичные чудеса в режиме деформации сдвига (кнопка 10):

Рис.13. Поперечная деформация (сдвиг) кота

Перед рисованием инициализируем матрицы TXForm и в зависимости, от того что требуется, применяем ту или иную матрицу. Фрагмент из кода выше:

Аффинная композиция

В коде выше присутствует композиция матриц — CombineTransform. Последовательность преобразований такая — вначале деформация, потом поворот. Проинспектируем кнопкой 11.

Рис.14. Деформированный, повернутый, замученный кот

Сравним с деформацией на рис.8. Там мы делали композицию матриц руками (в интерфейсе – режим 8), теперь этим занимается Windows GDI.

Рис.15. Все правильно делаем

Перед вызовом функции DrawAffine, необходимо перевести центр системы координат в центр прямоугольника. Напомню, начало системы координат – это центр трансформации. Именно вокруг него вертится вселенная.

Это фрагмент обработчика OnPaint того PaintBox, на котором рисуем . Вначале идет вызов SetViewportOrgEx, что переводит начало координат в центр прямоугольника. Потом происходит коррекция прямоугольника области рисования OffsetRect(rct, -Trunc(pnt.X), -Trunc(pnt.y)), иначе все координаты «уплывут» вправо на величину (pnt.x, pnt.y), затем вызов DrawAffine.

Если б мышь знала… Координаты вершин

В приложении есть возможность таскать за некоторые вершины. Тут возникает проблема. Если применяем аффинное преобразование, координаты точек, за которые можно «ухватиться» сильно отличаются от координат в «нормальном» состоянии координатной системы. Поэтому, перед тем как плоскость начнет изменяться, необходимо рассчитать нужные точки, т.е. координаты, понятные мышке.

И только после этого

Функции расчета достались в наследство от предыдущих этапов, когда экспериментировали над прямоугольником без применения аффинных преобразования. Не зря ж в конечном счете экспериментировали.

Конечно, можно сформировать и скомбинировать матрицы, взять коэффициенты и посчитать по формуле. Почти как в CalcComboPoints.

В GDI+ в TGPMatrix для этих целей существуют методы:

Здесь они не используются. Потом как-нибудь обязательно вернемся к ним.

Смещать ли начало координат?

Теоретически рекомендуется делать именно так, смещать и потом трансформировать. И, возможно, это правильно. Но можно обойтись и без этого. Просто привычней работать в «обычной» системе координат, когда точка (0,0) системы находится в левом верхнем углу.

По сути, как это делается, мы уже рассмотрели в самом начале статьи, когда вращали прямоугольник, считали координаты вершин и смещали в нужное место. Давайте это сделаем с помощью аффинных преобразований.

Порядок действий таков:

1. Определяемся с прямоугольником, в котором что-то хотим нарисовать
2. Определяемся с центром трансформации (pnt), т.е. точкой, вокруг которой будет происходить трансформация
3. Смещаем прямоугольник на -pnt.x, -pnt.y, тем самым совмещая центр трансформации с началом координат
4. Формируем матрицу трансформации
5. Добавляем матрицу перемещения с параметрами (или просто инициализируем в текущей матрице) eDx=pnt.x, eDy=pnt.y
6. Рисуем в получившемся смещенном прямоугольнике

Сильно сократил код за счет того, что не использую TXForm, а инициализирую сразу TGPMatrix. Что тут изменилось. В матрицу поворота добавил еще смещение в точку (ACenter.x, ACenter.y) – центр прямоугольника, или центр трансформации. Перед рисованием сместил прямоугольник отрисовки так, чтобы он оказался центрирован по началу координат, т.е. точки (0,0). Аффинное преобразование отработает поворот и сместиться на указанные величины по x и y.

Т.е. произойдет ровно тоже самое, что мы делали руками, когда прибавляли координаты центра к расчетным значениям вершин.

В демонстрационном примере это режимы 12..14, которые визуально будут совпадать с 9..11, с той лишь разницей, что перевода центра координат не происходит.

Чтобы продемонстрировать, работоспособность метода, существует последний режим – 15. Помимо основного прямоугольника, рисуется звезда и текст под углом, обратным текущему. Текст в дополнение к повороту также подвергается масштабированию.

Рис.16. Аффинные преобразования в любой требуемой точке плоскости

Я грозился вернуться к теме поворота звезд. Говорил, что есть более правильные методы. Брутальная звезда имени Стетхама, помните? Так вот, наиболее правильным будет вращать звезды, и не только, через аффинное преобразование.

Процедура, отвечающая за рисовку всего этого хозяйства: