В окружности проведены две взаимно перпендикулярные диаметры

Геометрия | 10 — 11 классы

В окружности проведены два взаимно перпендикулярных диаметра AC и BD.

Определите вид четырех уголольника ABCD.

Ответ : КвадратОбъяснение : АС и BD — диагонали четырехугольника ABCD.

Центром окружности, точкой О, они делятся пополам.

Если в четырехугольнике диагонали делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.

Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Если в прямоугольнике диагонали перпендикулярны, то это квадрат.

Видео:№536. Через образующую цилиндра проведены две взаимно перпендикулярные плоскости.Скачать

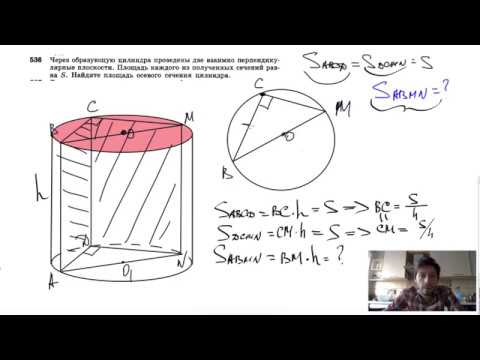
В окружности проведены два взаимно перпендикулярных диаметра АВ и СД?

В окружности проведены два взаимно перпендикулярных диаметра АВ и СД.

Точки F и K лежат на диаметре АИ на равном расстоянии от прямой СД .

Докажите, что отрезки F и DK равны.

Видео:№796. Из концов диаметра CD данной окружности проведены перпендикуляры СС1 и DD1 к касательнойСкачать

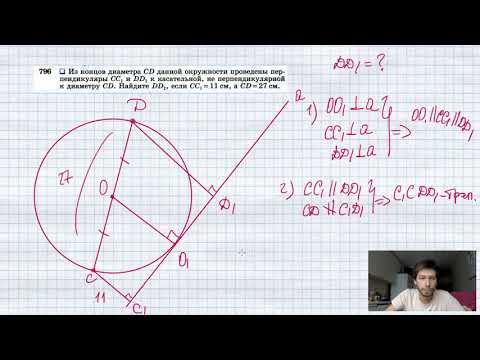
Диаметры AC и BD окружности взаимно перпендикулярны?

Диаметры AC и BD окружности взаимно перпендикулярны.

Последовательно соедините точки A, B, C, D.

Через эти точки проведите касательные к данной окружности Точки их пересечения оборзначьте A’ B’ C’ D’Назовите вид каждого из получившихся Четырехугольников относительно данной окружности.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда длинна которой 10 удалена от центра окружности на расстояние 4.

Видео:Математика ЕГЭ. В шаре проведены три перпендикулярных друг другу диаметраСкачать

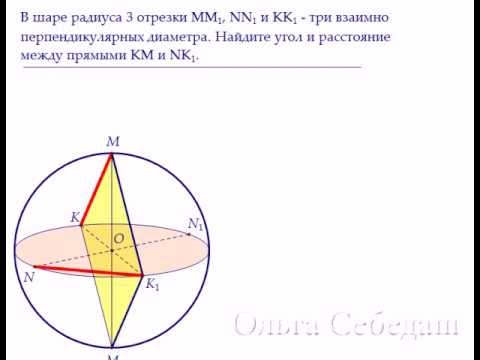
В AB и CD — два взаимно перпендикулярных диаметра окружности?

В AB и CD — два взаимно перпендикулярных диаметра окружности.

Хорда CB продолжена за точку B на отрезок BE, равный CB.

Каково взаимное расположение прямой DE и окружности?

Видео:№645. Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательнойСкачать

Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O?

Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O.

Докажите что четырехугольник ABCD — квадрат.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

AB и CD — взаимно перпендикулярные диаметры окружности?

AB и CD — взаимно перпендикулярные диаметры окружности.

Хорда CB продлена за точку B на отрезок BE, равный СВ.

Каково взаимное расположение прямой DE и окружности?

Видео:Задание 25 В круге проведены две перпендикулярные хордыСкачать

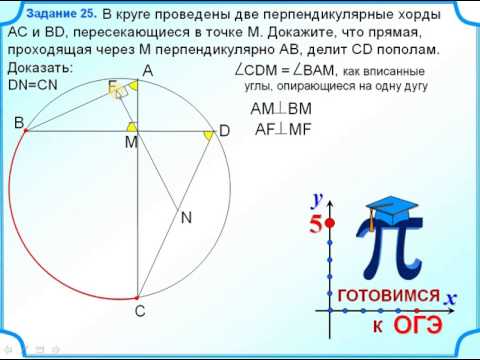
3. Сумма двух углов параллелограмма равна 150o?

3. Сумма двух углов параллелограмма равна 150o.

Найдите углы параллелограмма 4.

В ромбе ABCD прямая KL параллельна стороне АВ.

Определите виды четырёхугольников ABKL и KCDL 3.

Один из углов параллелограмма в 3 раза больше другого.

Найдите углы параллелограмма 4.

В окружности с центром в т.

О проведены два диаметра AB и CD.

Определите вид четырёхугольника ACBD.

3. Периметр параллелограмма равен 36 см, одна из его сторон равна 8 см.

Найдите остальные стороны параллелограмма.

4. В окружности с центром в т.

О проведены два взаимно перпендикулярных диаметра АВ и CD.

Определите вид четырёхугольника ABCD.

Видео:Как построить две взаимно перпендикулярные прямые с помощью циркуляСкачать

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру?

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру.

Докажите, что треугольники ADC и DBC равнобедренные.

Видео:Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности?

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности.

Видео:Длина окружности. Математика 6 класс.Скачать

Дана окружность?

Постройте взаимно перпендикулярные диаметры AB и CD.

Вы открыли страницу вопроса В окружности проведены два взаимно перпендикулярных диаметра AC и BD?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

FN, NM, EN, FM, EF. — вроде бы так.

Треугольник — часть плоскости, ограниченная трем точками, не лежащими на одной прямой. У него есть 3 вершины и 3 стороны.

Геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, нележащие на одной прямой.

Меньший угол треугольника лежит против меньшей стороны. Отрезки касательных, проведенных к окружности из одной точки, равны)) точка пересечения биссектрис — центр вписанной окружности)) радиус вписанной окружности можно найти из площади треугольника..

Пусть АВ = ВС = 2х, тогда АН = НС = х. 2х + 2х + х + х = 18 6х = 18 х = 3 S = 1 / 2 * а * h S = 1 / 2 * 3 * 3 = 4, 5 см ^ 2.

Высота это прямая делящая противоположную сторону от угла пополам и даёт 90°.

Видео:Перпендикуляр к прямой через заданную точку.Скачать

В окружности проведены две диагонали

Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

В окружности проведены две диагонали

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4. ^ $$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4. ^ $$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4. ^ $$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4. ^ $$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4. ^ $$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4. ^ $$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4. ^ $$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4. ^ $$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4. ^ $$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4. ^ $$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4. ^ $$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4. ^ $$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4. ^ $$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4. ^ $$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4. ^ $$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4. ^ $$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4. ^ $$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4. ^ $$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4. ^ $$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:Задача по геометрии из ОГЭ - пример решения задачиСкачать

В окружности проведены две диагонали

2021-11-23
В окружность вписаны две трапеции. Основания и боковые стороны одной из них соответственно параллельны основаниям и боковым сторонам другой.
а) Докажите, что диагонали одной трапеции равны диагоналям другой.
б) Найдите отношение площадей этих трапеций, если известно, что боковая сторона одной из них равна радиусу окружности, а боковая сторона другой в два раза меньше.

а) Обе трапеции равнобедренные, т.к. они вписаны в окружность. Пусть трапеция $ABCD$ с основаниями $AD$ и $BC$ и трапеция $KLMN$ с основаниями $KN$ и $LM$ вписаны в окружность радиуса $R$ (рис.1), причём $ADparallel KN$, $ABparallel MN$ и $CDparallel KL$. Тогда $angle ADC=angle LKN$ как углы с соответственно сонаправленными сторонами. По теореме синусов $AC=2Rsinangle ADC$ и $LN=2Rsinangle LKN$. Следовательно, $AC=LN$.
б) Обозначим $angle ADC=angle LKN=alpha$ (рис.2). Пусть $KL=R$, $AB=frac $. Проведём высоту $LP$ трапеции $KLMN$ и высоту $BH$ трапеции $ABCD$. Тогда отрезки $NP$ и $DH$ равны средним линиям соответствующих трапеций. Из прямоугольных треугольников $KPL$ и $AHB$ находим, что

а из прямоугольных треугольников $LPN$ и $BHD$ —

Проекция диагонали равнобедренной трапеции на основание равна полусумме оснований, т.е. $frac =NP$ и $frac =DH$. Значит,

$S_ =NPcdot LP=Rsqrt sinalphacdot Rsinalpha=R^ sqrt sin^ alpha,$

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

В окружности проведены две взаимно перпендикулярные диаметры ас и вд определите вид четырехугольника

Видео:Геометрия В окружности проведены две хорды AB = a и AC = b. длина дуги AC вдвое больше длины дуги ABСкачать

В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Ваш ответ

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,742
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В окружности проведены два взаимно перпендикулярных диаметра AC и BD?

Геометрия | 10 — 11 классы

В окружности проведены два взаимно перпендикулярных диаметра AC и BD.

Определите вид четырех уголольника ABCD.

Ответ : КвадратОбъяснение : АС и BD — диагонали четырехугольника ABCD.

Центром окружности, точкой О, они делятся пополам.

Если в четырехугольнике диагонали делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.

Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Если в прямоугольнике диагонали перпендикулярны, то это квадрат.

Видео:Перпендикулярные прямыеСкачать

В окружности проведены два взаимно перпендикулярных диаметра АВ и СД?

В окружности проведены два взаимно перпендикулярных диаметра АВ и СД.

Точки F и K лежат на диаметре АИ на равном расстоянии от прямой СД .

Докажите, что отрезки F и DK равны.

Видео:задачи три признакаСкачать

Диаметры AC и BD окружности взаимно перпендикулярны?

Диаметры AC и BD окружности взаимно перпендикулярны.

Последовательно соедините точки A, B, C, D.

Через эти точки проведите касательные к данной окружности Точки их пересечения оборзначьте A’ B’ C’ D’Назовите вид каждого из получившихся Четырехугольников относительно данной окружности.

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда длинна которой 10 удалена от центра окружности на расстояние 4.

В AB и CD — два взаимно перпендикулярных диаметра окружности?

В AB и CD — два взаимно перпендикулярных диаметра окружности.

Хорда CB продолжена за точку B на отрезок BE, равный CB.

Каково взаимное расположение прямой DE и окружности?

Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O?

Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O.

Докажите что четырехугольник ABCD — квадрат.

AB и CD — взаимно перпендикулярные диаметры окружности?

AB и CD — взаимно перпендикулярные диаметры окружности.

Хорда CB продлена за точку B на отрезок BE, равный СВ.

Каково взаимное расположение прямой DE и окружности?

3. Сумма двух углов параллелограмма равна 150o?

3. Сумма двух углов параллелограмма равна 150o.

Найдите углы параллелограмма 4.

В ромбе ABCD прямая KL параллельна стороне АВ.

Определите виды четырёхугольников ABKL и KCDL 3.

Один из углов параллелограмма в 3 раза больше другого.

Найдите углы параллелограмма 4.

В окружности с центром в т.

О проведены два диаметра AB и CD.

Определите вид четырёхугольника ACBD.

3. Периметр параллелограмма равен 36 см, одна из его сторон равна 8 см.

Найдите остальные стороны параллелограмма.

4. В окружности с центром в т.

О проведены два взаимно перпендикулярных диаметра АВ и CD.

Определите вид четырёхугольника ABCD.

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру?

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру.

Докажите, что треугольники ADC и DBC равнобедренные.

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности?

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности.

Дана окружность?

Постройте взаимно перпендикулярные диаметры AB и CD.

Вы открыли страницу вопроса В окружности проведены два взаимно перпендикулярных диаметра AC и BD?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Чтобы найти площадь параллелограмма нужно знать его высоту. Проведём ее ВН = > треугольник АНD — прямоугольный. Сумма острых углов прямоугольного треугольника равна 90 градусов = > угол ВDA = 90 — 45 = 45 грудусов = > AH = HD По теореме Пифагора на..

Sin 30 = 1 / 2 . 45 = (корень из двух) / 2. 60 = (корень из трех) / 2 cos 30 = (корень из 3) / 2 . 45 = (корень из двух) / 2. 60 = 1 / 2 tg 30 = (корень из трех) / 3 . 45 = 1 . 60 = корень из трех.

1) квадрат, тк у него все стороны и углы равны. 2)Р = (а + б)•2 Р = (х + х + 4)•2 Р = 4х + 8 Меньшая сторона 2 3)D = 120 тк углы у одной стороны образуют 180 * , тогда 180 — 60 = 120 4)3 стороны, тк только у треугольника может быть один тупой угол, ..

Часть 2. 9. Квадратом. 10. 12 см ((28 — 4) : 2) 11. 120 градусов, т. К. угол В = угол D 12. 5 сторон. 13. 16 см.

Они равны потому что параллельны, для этого можно провести измерения. Удачной учёбы.

В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.

В 13:42 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Вопрос вызвавший трудности

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Федотова Богдана Антоновна — автор студенческих работ, заработанная сумма за прошлый месяц 52 123 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.

В 13:42 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Вопрос вызвавший трудности

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Федотова Богдана Антоновна — автор студенческих работ, заработанная сумма за прошлый месяц 52 123 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.