Число пи окружность земли

Перевод статьи на английский язык, любое использование опубликованного в статье материала и упоминание о статье в англоязычных публикациях без разрешения автора запрещается!

1.
Когда Аристарх Самосский сказал, что Земля вращается, древние греки его упрекнули: «Вот же очевидное – солнце встаёт на одной стороне, бежит по небу весь день и садится на другой стороне. Так не морочь нам голову, мы видим, что солнце вращается вокруг нас на неподвижной Земле!»
Если сегодня кто-то скажет, что окружностей в действительности не бывает, что всякая окружность – это многоугольник с огромным, но конечным числом сторон, на него посмотрят, в лучшем случае, как на чудака: «Вот же очевидное – мы рисуем циркулем замкнутую линию. Так не морочь нам голову, мы видим, что это окружность!»

Любая окружность – это замкнутая линия, которая является границей круга в плоскости и возникает как траектория вращательного движения (вращения), а именно – как результат постоянного изменения направления перемещения в одну и ту же сторону на один и тот же постоянный угол. То есть изменяется не перемещение – этот процесс как происходил, так и продолжается, – а изменяется только направление перемещения! Если, к примеру, объект двигался с постоянной скоростью по инерции в какой-то своей инерциальной системе, то он так и продолжает в этой системе своё прямолинейное движение, а вот система (вместе с объектом, естественно) не сама, а под чьим-то воздействием поворачивает относительно определённого центра в пространстве. И в результате её поворота в пространстве объект в этом же пространстве изменяет направление своего перемещения. Таким образом, рассматривая вращение как процесс, мы обязательно имеем в виду не менее двух систем отсчёта – одну инерциальную и другую неинерциальную, в которой вращается инерциальная система. И замкнутая траектория вращения – линия, по которой перемещается вращающееся вокруг центра физическое тело, – образована одновременным движением тела и движением системы, которой это тело принадлежит.

Простейшее движение, а именно, перемещение материального объекта обеспечивается инерционными частицами – квантами материи, – так как они способны перемещаться только прямолинейно. А вращение объекта является результатом воздействий на него другого объекта или объектов. И если одно изменение направления – поворот – есть следствие одного воздействия, то вращение как постоянное изменение направления является, конечно, следствием воздействий, совершаемых с постоянной частотой. Так как каждое воздействие определяется в пространстве точкой приложения силы, то окружность – как траектория равномерного с постоянной скоростью перемещения физического тела – состоит из точек изменения направления и прямых отрезков перемещения одинаковой длины между этими точками, то есть является, в действительности, правильным многоугольником с очень большим количеством сторон очень малой длины.

2.
Считая, что угловое перемещение «ф» (греческая буква «фи») объекта вокруг центра системы равно отношению полного угла к количеству N угловых перемещений, мы пользуемся обозначением полного угла в радианах через двойное число «п» (греческая буква «пи»)
ф = 2п/N,
но это выражение является верным лишь в том случае, если мы под буквой «пи» подразумеваем развёрнутый угол в градусах, потому что, в отличие от точного значения полного угла в градусах (360), число «пи» не является точным постоянным значением (константой) для всех систем движения и не равно «N*ф/2», а вычисляется через синус половины измеренного угла перемещения
п = N*sin(ф/2).
Лишь для неизмеримо малых углов мы допускаем, что синус угла равен самому углу, то есть длина дуги равна стороне многоугольника, и тогда
sin(ф/2) = ф/2,
но надо помнить, что это – всего лишь наше допущение, которое не должно влиять на точность расчётов.

Мы привыкли определять иррациональное число «пи» как отношение длины окружности, которая всегда измерена приблизительно из-за постоянных поворотов, к длине её прямолинейного диаметра, измеряемого более точно, – это «геометрический», и, можно сказать, приближённый смысл числа. Но физический смысл его глубже, он определяется движением материальных объектов в пространстве. Число «п» («пи») – это отношение суммарной длины перемещения квантов материи, участвующих в процессе обращения материального объекта вокруг центра системы, к длине диаметра системы
п = NL/D = Nхd/nd = Nsin(ф/2),
где N=360/ф – количество сторон правильного многоугольника, образованного отрезками перемещения квантов материи, целое число;
ф (греческая буква «фи») – угловое перемещение кванта материи (угол, на который смещается в перспективе квант при «наблюдении» за ним из центра), может определяться непосредственным измерением угла или может определяться как отношение измеренной длины дуги, соответствующей стороне многоугольника, к измеренному радиусу окружности, описывающей многоугольник;
D = nd – длина максимальной диагонали в многоугольнике или диаметр круга, в который вписан правильный многоугольник, n – количество (целое число) фундаментальных длин в диаметре;
L = хd – расстояние перемещения кванта материи как длина стороны правильного многоугольника, х – количество (целое число) фундаментальных длин в стороне многоугольника;
d – фундаментальная длина.
Так как длина стороны вписанного многоугольника вычисляется через синус половины угла перемещения кванта материи
L=D*sin(ф/2),
отсюда следует, что
sin(ф/2) = х/n,
где «х» и «n» – целые числа.

3.
Можно однозначно утверждать, что в любой неинерциальной системе с вращательным движением вычисляемое значение числа «пи» будет иметь максимальное значение для данной системы, если длина стороны правильного многоугольника, по которому движется (обращается вокруг центра) объект, равна фундаментальной длине «d», то есть, при х=1 и L=d,
п = Nsin(ф/2) = (360/ф)*sin(ф/2).
И так как с увеличением диаметра системы и соответственным увеличением числа «n» увеличивается также и число N (ведь при таком условии «N = п*n»), то степень точности максимального значения числа «пи» увеличивается пропорционально увеличению размеров системы и для каждой системы отсчёта имеет свой предел, поскольку каждая система имеет максимальный диаметр (конечную протяжённость), выраженный, соответственно, предельным целым числом «n». Например, начиная с систем вращения с минимальными диаметрами, число «пи» будет принимать следующие значения:
при ф =180 градусов, N=2 («двухугольник» = диаметр плоской мельчайшей фигуры), n=1, пи=2,
при ф=120 гр, N=3 (треугольник с min длиной стороны), n меньше 2, п=3^(3/2)/2, прибл. 2,598,
при ф=90 гр, N=4 (квадрат с минимальной длиной стороны), n меньше 2, п=2^(3/2) , приблиз. 2,8284,
при ф=72 гр, N=5 (пятиугольник с min длиной стороны), n меньше 2, п = примерно 2,9389,
при ф=60 гр, N=6 (шестиугольник с min длиной стороны), n = 2, пи = 3,
при ф=51,4 гр, N=7 (семиугольник с min стороной), n меньше 3, пи = примерно 3,0372,
при ф=45 гр, N=8 (восьмиугольник с min стороной), n меньше 3, пи = примерно 3,0615,
при ф=40 гр, N=9 (девятиугольник с min стороной), n меньше 3, пи = примерно 3,0782,
при ф=36 гр, N=10 (десятиугольник с min стороной), n меньше 4, пи = примерно 3,0902,
при ф=32,7 гр, N=11 (одиннадцатиугольник с min стороной), n меньше 4, пи = прибл. 3,0991,
при ф=30 гр, N=12 (двенадцатиугольник с min стороной), n меньше 4, пи = прибл. 3,1058,
…
при ф=24 гр, N=15 (пятнадцатиугольник с min стороной), n меньше 5, пи = прибл. 3,1187,
…
при ф=18 гр, N=20 (двадцатиугольник с min стороной), n меньше 7, пи = прибл. 3,1287,
…
при ф=10 гр, N=36 (тридцатишестиугольник с min стороной), n меньше 12, пи = прибл. 3,1376,
…
при ф=6 гр, N=60 (шестидесятиугольник с min стороной), n меньше 20, пи = прибл. 3,1402,
…
при ф=2 гр, N=180 (ставосьмидесятиугольник с min стороной), n меньше 58, пи = прибл. 3,1414,
…
при ф=1 градус, N=360 (тристашестидесятиугольник с min стороной), n меньше 115, пи = прибл. 3,14155,
и так далее.

Так как в заявленных условиях количество сторон N – линий движения квантов материи – равно произведению числа «пи» и количества фундаментальных длин в диаметре, которое по условию должно быть представлено целым числом «n»,
N=п*n,
то очевидно, что, кроме движения по окружности как по шестиугольнику, движение в остальных «рассчитанных» выше системах реально может совершаться лишь по эллипсу или спирали, то есть данные системы не могут представлять окружность. А настоящие окружности как «многоугольники движения» могут реально проявляться лишь в системах, где длина стороны многоугольника уже больше одной фундаментальной длины, то есть, при х=2 и больше. Но эта тема – движение в неинерциальных системах и возможности такого движения (вращения и обращения вокруг центра) – будет освещена, а частично уже раскрыта в других статьях по логофизике.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

15 интересных фактов о числе Пи, о которых вы, возможно, не знали

Пи считается хлебом с маслом для математиков и инженеров. Это буквально круто, немного странно, но круто. Число Пи является математической константой, и оно определяет отношение между окружностью круга и его диаметром. С начала 19-го века (наиболее вероятно с середины 18-го века), это было обозначено греческой буквой «π». Это некоторые известные вещи о пи, но как насчет вещей, которые ты не знаешь? Хотите узнать некоторые неизвестные факты об этом интересном номере? Давайте наполним вас некоторыми интересными фактами о числе Пи.

Видео:ОКРУЖНОСТЬ И КРУГ // ДЛИНА ОКРУЖНОСТИ // ЧИСЛО ПИСкачать

11. Ваши банковские реквизиты можно найти в пи

Что ж, мы знаем, что число Пи является иррациональным числом, то есть его десятичное представление может длиться вечно. Технически, каждое возможное число, которое вы можете придумать, находится где-то в нем. Это включает в себя ваш контактный номер, дату рождения, номер вашего шкафчика и даже ваши банковские реквизиты. Более того, если у нас будет достаточно цифр, использование алгоритма, который может преобразовывать числа в буквы, позволит нам найти Библию, полное собрание сочинений Шекспира и Чосера или любую книгу, когда-либо написанную.

Видео:Число Пи-здесь. Объяснение математического смысла.Скачать

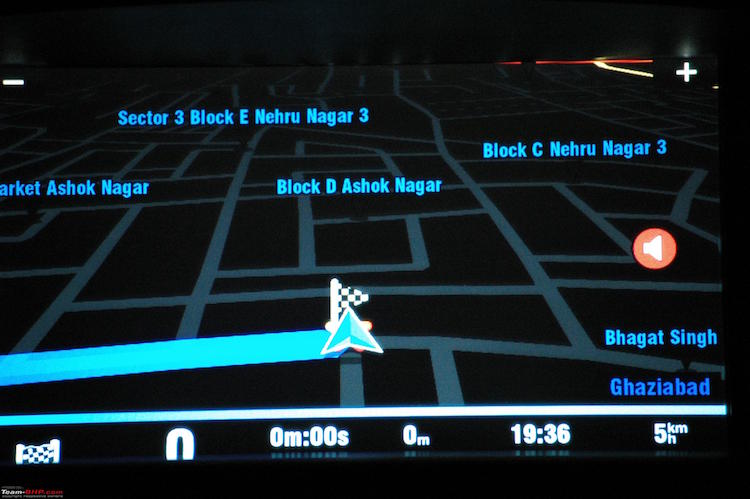
10. Использует в навигации

Пи играет важную роль в системах наведения, установленных на спутниках и космических станциях. Из всего, навигация в космосе на самом деле требует высокой точности. Для каждой вычисляемой десятичной цифры мы получаем большую точность. Но насколько мы должны быть точными, чтобы все работало правильно? Сьюзан Гомез из НАСА, управляющего Международной космической станцией по навигации, навигации и управлению (GNC), сообщает, что в большинстве расчетов с использованием Пи используются 15 цифр для GNC и 16 цифр для космической интегрированной системы глобального позиционирования / инерциальной навигационной системы (SIGI).

Видео:Что такое число Пи? Кто его изобрел и почему оно так важноСкачать

9. Истинная площадь круга никогда не может быть известна

Только в начале 18-го века мы смогли доказать, что число впервые является иррациональным числом. Может показаться привлекательным видеть Пи как просто соотношение между окружностью и диаметром, но оно всегда иррационально (диаметр — это целое число, тогда окружность — нет). Это означает, что мы никогда не сможем узнать фактическую окружность и, в конечном счете, площадь круга.

Видео:Как считали число пи? [Veritasium]Скачать

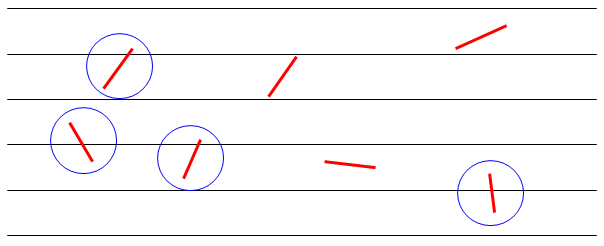
8. Игла Буффона

Игла Буффона или просто проблема с иглой в вероятности была впервые указана Жоржем-Луи Леклерком, графом де Буффоном, в 18-м веке, когда падение иглы на лист, отмеченный линиями, определит вероятность того, что игла пересечет линию на странице. Важно отметить, что вероятность результата эквивалентна значению числа Пи.

Давайте разберемся с этим. В этом случае на самом деле есть две переменные: угол наклона иглы, давайте присвоим ему символ тета (θ) и расстояние между ближайшей линией и центральной точкой иглы. Тета может варьироваться от 0 ° до 180 °, который измеряется параллельно нарисованным линиям.

Выяснилось, что вероятность того, что игла прорежет линию при посадке, составляет ровно 2 / Пи или почти 64%. Это означает, что число Пи можно как-то рассчитать, используя технику Буффона, если у кого-то будет достаточно времени и терпения, чтобы пройти все симуляции. Чтобы понять это намного лучше, вы можете попробовать это.

Видео:Длина окружности. Математика 6 класс.Скачать

7. Отношения между извилистыми реками и Пи

У Пи неожиданные отношения со многими явлениями в этом мире, включая извилистые реки. Как? Что ж, путь любой реки в основном описывается ее извилистостью, способностью изгибаться, перемещаться назад и вперед по ее пойме. Математически говоря, это длина извилистого пути, деленная на длину реки от начала до конца. Оказывается, что средняя река имеет извилистость числа Пи независимо от ее длины или количества поворотов на своем пути.

Видео:ЧИСЛО БОГА, УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ [Число ПИ и Скатерть Улама]Скачать

6. Преобразование Фурье и обработка сигналов

Пи играет еще одну очень важную роль в области «обработки сигналов». Это просто анализ, синтез и модификация сигналов. Но здесь действует сложная система. Эта сложная система представляет собой «преобразование Фурье», которое преобразует сигналы в частотный спектр. Мобильный телефон каждого, будь то его андроид или iPhone, выполняет преобразование Фурье, когда он связывается с местной сотовой вышкой.

Кроме того, формула оценивается вашим мобильным телефоном в цифровом виде с помощью определенного алгоритма, известного как «быстрое преобразование Фурье» или «БПФ», который был открыт математиками в 1950-х годах. Важно отметить, что каждый процесс включает в себя число π. Так что технически, есть определенное значение Пи где-то в вашем телефоне, будь то простой или смартфон.

Видео:#182. Постижение числа π (feat. Алексей Савватеев)Скачать

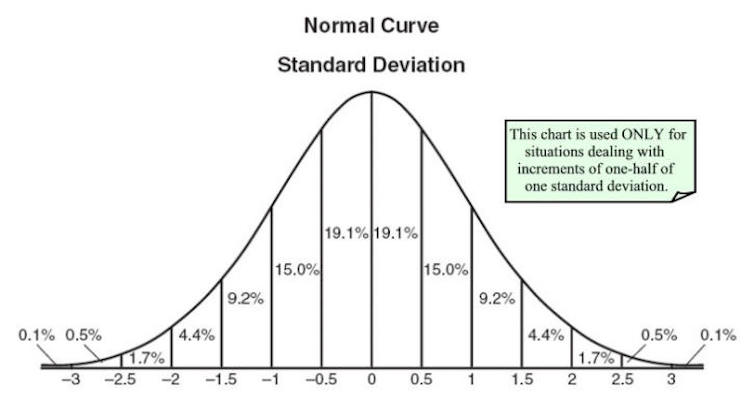
5. Распределение вероятностей

Пи также играет важную роль в нормальном распределении вероятностей. Без сомнения, вы сталкивались с таким распределением вероятностей не один, а много раз. Они важны и часто используются в различных областях исследований, включая математику, физику и общественные науки. Это то, что вам нужно, от прогнозирования результатов теста ученика до измерения отдаленных сверхновых звезд.

Это правило большого пальца: всякий раз, когда вы видите, как Пи подкрадывается где-то в любом уравнении, убедитесь, что где-то в этом спрятан круг. В этом случае Пи вводится через интеграл Эйлера – Пуассона, который содержит квадратный корень из Пи.

Видео:О жизни двух главных констант математикиСкачать

4. Проблема с лентой

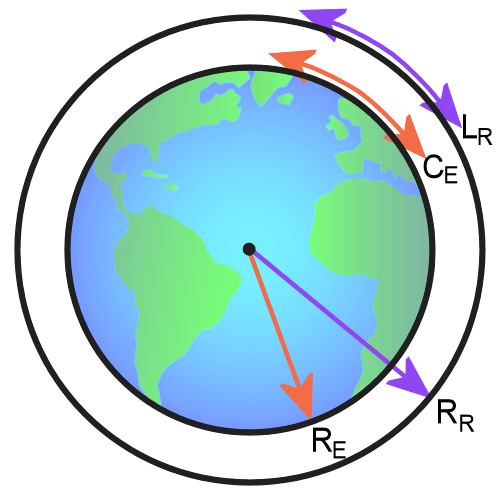
Предположим, вы хотите обернуть вокруг Земли ленту на экваторе, длина окружности которого составляет 24 900 миль (идеальная сфера). Теперь попытайтесь выяснить, сколько потребуется ленты, которая могла бы окружить Землю на расстоянии одного дюйма над ее поверхностью. Можно легко подумать, что для этого потребуется огромное количество ленты. Но на самом деле это не так. Мы расскажем вам, как.

Еще раз предположив, что Земля является идеальной сферой, у нас будет круг с окружностью 24 900 миль (на экваторе). Это означает, что радиус будет 24 900 / (2 * пи) или примерно 3963 миль. Теперь вторая лента, на дюйм выше поверхности Земли, будет иметь радиус на один дюйм больше радиуса Земли, что дает нам уравнение C = 2 Пи (r + 1) или C = 2 Пи (r) + 2 Пи.

Отсюда можно сказать, что окружность второй ленты увеличится на 2Пи. Фактически, независимо от того, какой первоначальный радиус увеличивает радиус, всегда будет 2Пи.

Видео:Число Пи не перестает удивлять!Скачать

3. Последовательность Фибоначчи и вычисление числа Пи

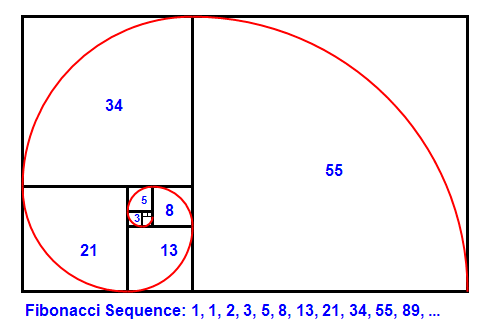
Долгое время вычисления числа Пи основывались на двух методах: первый был разработан Архимедом, а второй был разработан Джеймсом Грегори, шотландским математиком в 1671 году. Однако оказывается, что последовательность Фибоначчи также может быть эффективно использована для вычисления значение Пи.

Последовательность Фибоначчи — это числовая последовательность, в которой число создается или определяется путем добавления двух чисел перед ним. Последовательность начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и продолжается бесконечно. Поскольку арктангенс 1 равен Пи / 4, переставляя уравнение в arctan (1) * 4 = Пи, мы также можем продемонстрировать Пи в терминах чисел Фибоначчи.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

2. Самый первый расчет

Считается, что Пи был первоначально открыт древними вавилонянами около 4000 лет назад. Согласно Rhind Papyrus, древние египтяне вычислили значение Пи как приблизительно 3.1605. Но первый зарегистрированный метод для вычисления значения числа Пи был разработан греческим математиком Архимедом Сиракузским в 250 году до нашей эры.

Архимед грубо рассчитал площадь круга, найдя области двух отдельных многоугольников правильного размера. Один был вписан в круг, а другой — внутри того круга, в котором он был очерчен. Таким образом, два полигона обеспечивали верхнюю и нижнюю границы площади круга (фактическая площадь круга лежит между областями вписанных и описанных многоугольников).

Архимед знал о том факте, что он не обнаружил фактическое значение Пи, а лишь приблизительное значение в этих пределах. Таким образом, Архимед показал, что число Пи между 3 1/7 и 3 10/71. Этот алгоритм строго использовался учеными и инженерами на протяжении 1000 лет, из-за чего даже сегодня его иногда называют «постоянной Архимеда».

Видео:Длина окружности. Площадь круга, 6 классСкачать

1. Скрытая связь между квантовой механикой и Пи

Физики недавно обнаружили связь между многовековой известной математической формулой Пи и квантовой механики, которая скрывалась годами. Это было в 1665 году, когда известный британский математик Джон Уоллис представил свою собственную версию формулы вычисления Пи. Исследователи из Университета Рочестера считают, что они нашли ту же формулу, скрывающуюся при расчете энергетических уровней атома водорода.

Краткие факты

С 1998 года, каждый год 14 марта, научное сообщество празднует день Пи. Этот конкретный день был выбран из-за его соответствия с 3.14, который является пи значение. Первое широко посещаемое празднование дня пи было организовано физиком Ларри Шоу. Интересно, что Альберт Эйнштейн родился 14 марта 1879 года.

В 2002 году группа японских исследователей из Токийского университета вычислила 1,24 триллиона цифр числа пи, используя мощный суперкомпьютер Hitachi SR 8000, побив все предыдущие рекорды.

По мнению некоторых математиков, вместо того чтобы называть его Безугловым, гораздо правильнее сказать, что круг имеет бесконечное число углов.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Сила “пи”: 10 фактов о числе π

1. С развитием компьютерных технологий значение числа пи было вычислено до 4 миллиардов знаков после запятой, но для упрощения его обычно принимают равным 3,14. Это число в том или ином виде было известно ученым многих древних цивилизаций, но чаще всего его принимали равным 3. Впрочем, это уже где как – в Древнем Египте, например, значение числа пи равнялось 3,162, а в Древнем Китае – 3,1459.

2. В конце XIX века в США, штат Индиана, едва не был принят абсурдный закон, согласно которому значение числа пи на территории штата устанавливалось равным 3,2. Но возмущение научного сообщества подобным отношением к математике привело к тому, что законопроект в итоге так и не был принят.

3. Число пи бесконечно, как сама Вселенная. Оно иррационально, и в десятичной системе счисления не может быть выражено в виде конечного количества цифр. Наращивание компьютерной мощности может позволить только получить его уточненное значение, но никак не конечное.

4. Современное название это число получило только в XVIII веке стараниями европейских ученых Уильяма Джонса и Леонарда Эйлера. Причем греческая буква π была выбрана не случайно – с нее начинаются греческие слова “окружность” и “периметр”. А число пи, как известно, равно отношению длины окружности (периметра) к ее диаметру.

5. Самым древним летописным упоминаниям о числе пи уже около 4500–5000 лет. Некоторые ученые даже полагают, что библейская история про Вавилонскую башню вполне реальна, и это число использовалось при ее возведении, но из-за ошибок в расчетах башня обрушилась.

6. В мире существуют клубы поклонников числа пи, и даже проводятся соревнования, побеждает в которых тот, кто в правильной последовательности назовет наибольшее количество знаков после запятой. Занятие, может быть, и не слишком практичное, зато оно отлично тренирует память. Рекордсменом является японский инженер по имени Акира Харагучи, который сумел запомнить 111 701 знак после запятой. Для запоминания такого массива чисел Харагучи использовал мнемоническую методику собственного изобретения.

7. В 1988 году одна американская газета выпустила заметку о том, что правительство штата Алабама решило сократить число пи до трех. Это известие шокировало все научное сообщество, но вскоре выяснилось, что это был розыгрыш на 1 апреля.

8. Числу пи даже посвящено несколько памятников, большинство выполнено в виде греческой буквы π того или иного размера. Самый известный из них можно увидеть в США, в городе Сиэттл. Там монумент установлен у входа в Музей искусств.

9. Из всех ученых древности первым способ для вычисления значения числа пи предложил Архимед. Для этого он использовал окружность и правильные многоугольники, которые вписывал в нее и описывал вокруг нее, приняв диаметр окружности за условную единицу. В таком случае длина сторон многоугольников внутри окружности соответствовала нижней оценке длины окружности, а длина сторон наружных многоугольников – ее верхней оценке.

10. Как уже сказано выше, число пи бесконечно. Но даже в тех его знаках после запятой, что уже известны человечеству, можно найти любую последовательность цифр, от номера телефона вашей бабушки до точной даты рождения любого человека на Земле.

📽️ Видео

Число ПиСкачать

+Как найти длину окружностиСкачать

Тайна числа 1.618034 - самое ВАЖНОЕ число в миреСкачать

Число Пи: как найти его с точностью до 50 знака?Скачать

Как Эратосфен измерил диаметр Земли?Скачать

Длина окружности и площадь круга. Что такое число пи ?Скачать

Что означает число Пи?Скачать