В окружности проведены 2 диагонали

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

В окружности проведены 2 диагонали

2021-11-23
В окружность вписаны две трапеции. Основания и боковые стороны одной из них соответственно параллельны основаниям и боковым сторонам другой.
а) Докажите, что диагонали одной трапеции равны диагоналям другой.
б) Найдите отношение площадей этих трапеций, если известно, что боковая сторона одной из них равна радиусу окружности, а боковая сторона другой в два раза меньше.

а) Обе трапеции равнобедренные, т.к. они вписаны в окружность. Пусть трапеция $ABCD$ с основаниями $AD$ и $BC$ и трапеция $KLMN$ с основаниями $KN$ и $LM$ вписаны в окружность радиуса $R$ (рис.1), причём $ADparallel KN$, $ABparallel MN$ и $CDparallel KL$. Тогда $angle ADC=angle LKN$ как углы с соответственно сонаправленными сторонами. По теореме синусов $AC=2Rsinangle ADC$ и $LN=2Rsinangle LKN$. Следовательно, $AC=LN$.
б) Обозначим $angle ADC=angle LKN=alpha$ (рис.2). Пусть $KL=R$, $AB=frac$. Проведём высоту $LP$ трапеции $KLMN$ и высоту $BH$ трапеции $ABCD$. Тогда отрезки $NP$ и $DH$ равны средним линиям соответствующих трапеций. Из прямоугольных треугольников $KPL$ и $AHB$ находим, что

а из прямоугольных треугольников $LPN$ и $BHD$ —

Проекция диагонали равнобедренной трапеции на основание равна полусумме оснований, т.е. $frac=NP$ и $frac=DH$. Значит,

$S_=NPcdot LP=Rsqrtsinalphacdot Rsinalpha=R^sqrtsin^alpha,$

Видео:№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать

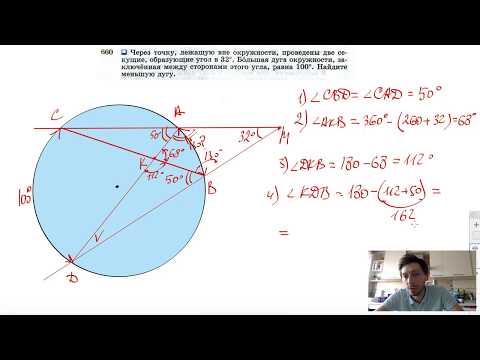
В окружности проведены два взаимно перпендикулярных диаметра AC и BD?

Геометрия | 10 — 11 классы

В окружности проведены два взаимно перпендикулярных диаметра AC и BD.

Определите вид четырех уголольника ABCD.

Ответ : КвадратОбъяснение : АС и BD — диагонали четырехугольника ABCD.

Центром окружности, точкой О, они делятся пополам.

Если в четырехугольнике диагонали делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.

Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Если в прямоугольнике диагонали перпендикулярны, то это квадрат.

Видео:Геометрия В окружности проведены две хорды AB = a и AC = b. длина дуги AC вдвое больше длины дуги ABСкачать

В окружности проведены два взаимно перпендикулярных диаметра АВ и СД?

В окружности проведены два взаимно перпендикулярных диаметра АВ и СД.

Точки F и K лежат на диаметре АИ на равном расстоянии от прямой СД .

Докажите, что отрезки F и DK равны.

Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Диаметры AC и BD окружности взаимно перпендикулярны?

Диаметры AC и BD окружности взаимно перпендикулярны.

Последовательно соедините точки A, B, C, D.

Через эти точки проведите касательные к данной окружности Точки их пересечения оборзначьте A’ B’ C’ D’Назовите вид каждого из получившихся Четырехугольников относительно данной окружности.

Видео:Задание 25 В круге проведены две перпендикулярные хордыСкачать

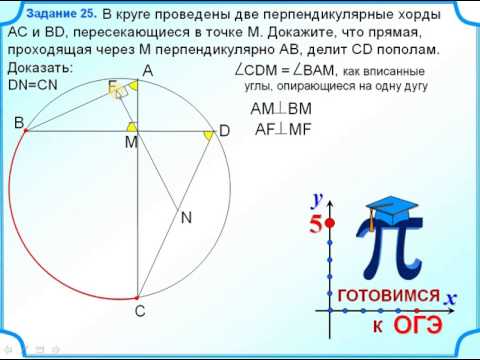
В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда длинна которой 10 удалена от центра окружности на расстояние 4.

Видео:№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать

В AB и CD — два взаимно перпендикулярных диаметра окружности?

В AB и CD — два взаимно перпендикулярных диаметра окружности.

Хорда CB продолжена за точку B на отрезок BE, равный CB.

Каково взаимное расположение прямой DE и окружности?

Видео:В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать

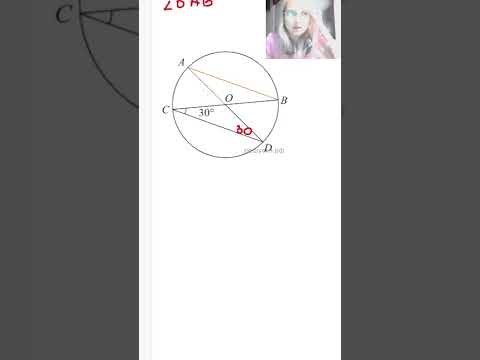
Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O?

Отрезки AC и BD — взаимно перпендикулярные диаметры окружности с центром в точке O.

Докажите что четырехугольник ABCD — квадрат.

Видео:через точку А, лежащую вне окружности проведены две прямые. Одна прямая касается.. ФИПИСкачать

AB и CD — взаимно перпендикулярные диаметры окружности?

AB и CD — взаимно перпендикулярные диаметры окружности.

Хорда CB продлена за точку B на отрезок BE, равный СВ.

Каково взаимное расположение прямой DE и окружности?

Видео:Геометрия В окружности с центром O проведены диаметр AB и хорда AC. Докажите, что угол BOC = 2 угламСкачать

3. Сумма двух углов параллелограмма равна 150o?

3. Сумма двух углов параллелограмма равна 150o.

Найдите углы параллелограмма 4.

В ромбе ABCD прямая KL параллельна стороне АВ.

Определите виды четырёхугольников ABKL и KCDL 3.

Один из углов параллелограмма в 3 раза больше другого.

Найдите углы параллелограмма 4.

В окружности с центром в т.

О проведены два диаметра AB и CD.

Определите вид четырёхугольника ACBD.

3. Периметр параллелограмма равен 36 см, одна из его сторон равна 8 см.

Найдите остальные стороны параллелограмма.

4. В окружности с центром в т.

О проведены два взаимно перпендикулярных диаметра АВ и CD.

Определите вид четырёхугольника ABCD.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру?

В окружности проведены диаметр АВ и хорда СD, перпендикулярная диаметру.

Докажите, что треугольники ADC и DBC равнобедренные.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности?

Какие из следующих утверждений верны : 1)Диагонали ромба взаимно перпендикулярны 2)Всякая хорда окружности меньше диаметра 3)Длина окружности более чем, в три раза, превышает диаметр этой окружности.

Видео:Геометрия В окружности проведены диаметры AB и CD. Докажите, что AC = BD и AC ll BDСкачать

Дана окружность?

Постройте взаимно перпендикулярные диаметры AB и CD.

Вы открыли страницу вопроса В окружности проведены два взаимно перпендикулярных диаметра AC и BD?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

У равнобедренного треугольника нет гипотенузы.

Треугольник FES = треугольникуSED по третьему признаку значит угол FES = углу SED и они равны по 45°. Угол FSE равен углу DSE и они равны по 90°. Угол SDE равен углу SFE и равны они по 45°.

А) ZAOB = 44° + 77° = 121°. Б) ZAOB = 12°37′ + 108 25 = 121°2′. Ответ, а) 121° ; б) 121°2′.

📽️ Видео

Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

В окружности с центром в точке O проведены диаметры ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Геометрия.Две хорды и окружность.ДиаметрСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Геометрия К окружности радиусом 12 см проведены две касательные, образующие прямой угол. ПрямаяСкачать

Геометрия Две окружности имеют общий центр O (см. рис.). В одной из окружностей проведен диаметр ABСкачать

Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых пересекаетСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать