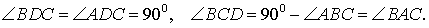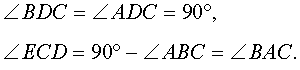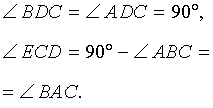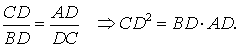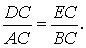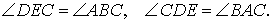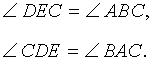Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники
- Запомните!
- Простые вопросы по теме «Треугольники»
- Непростые вопросы по теме «Треугольники»
- Ответы на простые и непростые вопросы
- Высота треугольника. Задача Фаньяно
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
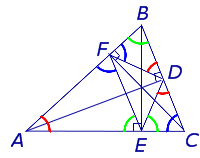
- Задача Фаньяно
- Метод ключевой задачи в геометрии 8 класса. материал для подготовки к егэ (гиа) по геометрии (8 класс) по теме
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 🎬 Видео
Запомните!
1. Признаки равенства треугольников.
- 1-й. По двум сторонам и углу между ними.
- 2-й. По стороне и двум прилежащим к ней углам.
- 3-й. По трем сторонам.
2. Свойство углов равнобедренного треугольника.
Углы при основании равнобедренного треугольника равны.
3. Обратная теорема.
Если два угла треугольника равны, то треугольник равнобедренный.
4. Свойство биссектрисы равнобедренного треугольника.
Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.
5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:
- а) высота является и медианой;
- б) высота является и биссектрисой;
- в) биссектриса является и медианой.
6. Теорема о свойстве точек серединного перпендикуляра.
- Любая точка серединного перпендикуляра равноудалена от концов отрезка.
- Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.
7. Теорема о пересечении серединных перпендикуляров.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.
Простые вопросы по теме «Треугольники»
- В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
- Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
- Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
- Может ли высота треугольника делить сторону пополам?
- Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
- Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
- Является ли любой равнобедренный треугольник равносторонним?
- Является ли любой равносторонний треугольник равнобедренным?
- Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
- Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
- Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
- Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
- Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
- Что для студентов означает слово «медиум»?
- Сколько всего теорем в данной теме?
Непростые вопросы по теме «Треугольники»
16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?
Ответы на простые и непростые вопросы
- Три. Два маленьких и один данный.
- 12; 24.
- Да.
- Да. В равнобедренном треугольнике.
- Да. В равнобедренном треугольнике.
- Нет. Только биссектриса, проведенная из вершины к основанию.
- Нет.
- Да.
- Да. Если треугольник равносторонний.
- Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
- Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
- Да. Например, равносторонний.
- 90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
- Медиум — студенческий праздник, знаменующий середину учебы.
- Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.
16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.
Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия:
Видео:8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Высота треугольника. Задача Фаньяно
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:Найти высоту дерева Задача на подобие треугольников 2 частьСкачать

Высота треугольника. Свойство высоты прямоугольного треугольника
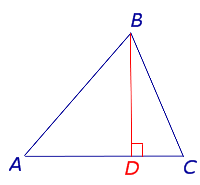
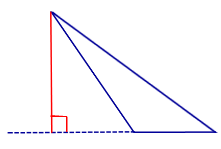
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
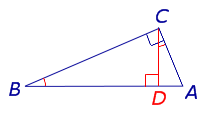
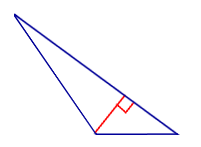
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
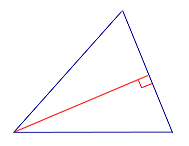
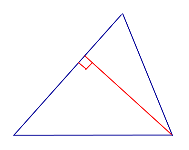
| Остроугольный треугольник | 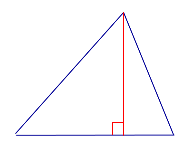 | Все высоты остроугольного треугольника лежат внутри треугольника. |
 | ||
 | ||
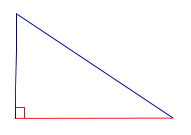
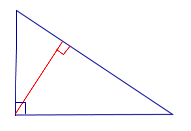
| Прямоугольный треугольник | 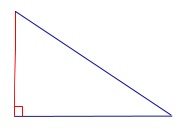 | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
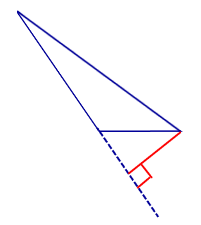
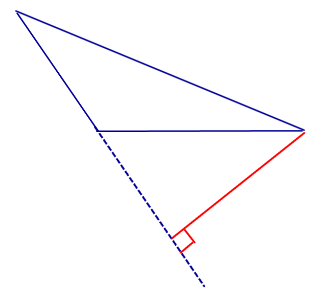
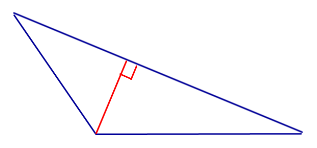
| Тупоугольный треугольник | 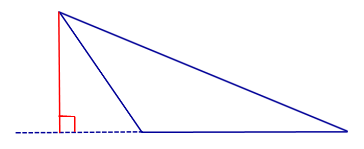 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
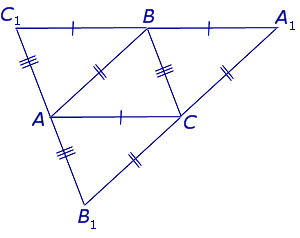
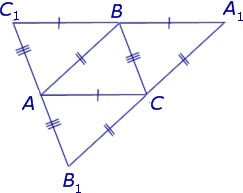
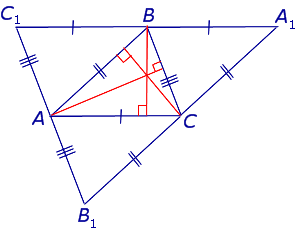
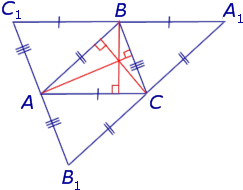
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание | |||
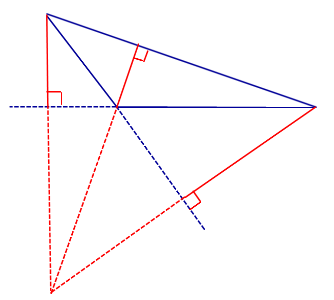
| Остроугольный треугольник | 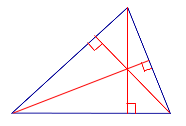 | ||||
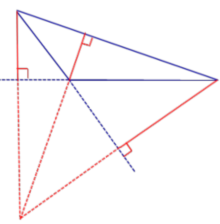
| Прямоугольный треугольник | 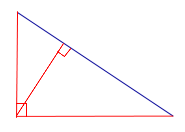 |
| Вложение | Размер |
|---|---|
| metod_klyuchevoy_zadachi.docx | 246.3 КБ |
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Предварительный просмотр:
Итоговое повторение курса планиметрии с привлечением метода ключевой задачи
Метод составления системы задач, построенной по принципу – каждая задача системы использует результат решения одной какой-либо (ключевой) задачи, будем называть методом ключевой задачи .
Существует две точки зрения на понятие ключевой задачи. Первая из них состоит в рассмотрении ключевой задачи как задачи-факта. Зачастую такая ключевая задача оказывается дополнительной теоремой школьного курса. Вторая точка зрения состоит в рассмотрении ключевой задачи как задачи-метода. При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме.
«Ключевая» задача является средством решения других задач, поэтому ее знание учащимися обязательно. Разворачивающаяся система задач, с одной стороны, способствует усвоению факта или метода решения, изложенных в «ключевой» задаче, с другой, позволяет увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная данным методом система задач является эффективным средством повторения, обобщения и систематизации учебного материала.
Ключевая задача. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
Д о к а з а т е л ь с т в о. Проведем CF , параллельно биссектрисе BD . Тогда по теореме о пропорциональных отрезках .
Треугольник BCF – равнобедренный.
Так как углы и равны как соответственные при параллельных прямых BD и CF и секущей AF , углы и равны как накрест лежащие при параллельных прямых BD и CF и секущей ВС , по свойству биссектрисы.
Следовательно, BF=BC . Тогда .
Если BD – биссектриса внешнего угла треугольника АВС , то .
Задача 1. В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки 3 и 4. Найдите площадь треугольника.
Р е ш е н и е. Пусть , . Тогда по свойству биссектрисы , а по теореме Пифагора . Решая систему получим: , . Вычисляя площадь треугольника по формуле , получим .
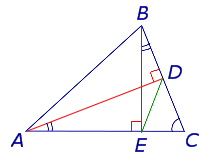
Задача 2. В прямоугольном треугольнике проведена биссектриса острого угла. Отрезок, соединяющий ее с основание с точкой пересечения медиан, перпендикулярен катету. Найдите острые углы треугольника.
Р е ш е н и е. Пусть AD – биссектриса прямоугольного треугольника АВС .
Точка О – точка пересечения медиан. Тогда по условию задачи .
По свойству медиан .
По теореме Фалеса .
Так как AD – биссектриса, то . Следовательно, .
Так как гипотенуза АВ в два раза больше катета АС , то . Следовательно, .
О т в е т: 30 0 ; 60 0 .
Задача 3. В равнобедренный треугольник АВС с основанием АС вписана окружность с центром О . Луч АО пересекает сторону ВС в точке К , причем , . Найдите периметр треугольника АВС .
Р е ш е н и е. Так как О – центр вписанной окружности, то АК – биссектриса треугольника АВС . Тогда . Имеем , .
Задача 4. В окружность радиуса см вписан треугольник АВС , в котором , а сторона АВ в два раза больше стороны АС . В треугольнике проведена биссектриса АМ . Найдите длину отрезка С.
Р е ш е н и е. АМ – биссектриса треугольника АВС . Тогда .
Чтобы воспользоваться свойством биссектрисы, необходимо найти длину стороны ВС. По теореме синусов . Отсюда .
Пусть , тогда . Имеем , откуда .
Задача 5. В треугольнике АВС проведена биссектриса ВЕ , которую центр О вписанной окружности делит в отношении . Найдите АВ , если , .
Р е ш е н и е. Так как О – центр вписанной окружности, то АМ и CD – биссектрисы.
По свойству биссектрисы треугольника ВСЕ , , .
По свойству биссектрисы треугольника АВЕ , , .
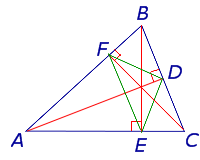
Задача 6. Найдите стороны треугольника, если медиана и высота, проведенные из одного угла, делят его на три равные части, а длина медианы равна 10.
Р е ш е н и е. Пусть СN – медиана, а СК – высота.
Так как СК – высота и биссектриса, то треугольник CNB равнобедренный, следовательно, и .
CN – биссектриса в треугольнике АСК , следовательно,
Треугольник – прямоугольный, поэтому , , , , .
Задача 7. Биссектриса BD внутреннего угла треугольника АВС равна 6, а биссектриса ВF смежного с ним угла равна 8. Найдите площадь треугольника АВС , если .
Р е ш е н и е. Биссектрисы смежных углов перпендикулярны, поэтому .
по теореме Пифагора.
По свойству биссектрисы .
Чтобы найти площадь треугольника АВС необходимо знать длину высоты ВМ , проведенной к стороне АС . Из треугольника BDF найдем . Тогда , .
Задачи для самостоятельного решения
1. В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5. Найдите площадь треугольника.
2. В треугольнике ВСЕ , . Отрезок СК – биссектриса треугольника. Найдите КЕ , если радиус описанной около треугольника окружности равен .
3. Дан треугольник АВС . Его высота BD равна 30. Из основания Е биссектрисы АЕ опущен перпендикуляр EF на сторону АС . Найдите длину этого перпендикуляра, если .
4. В треугольнике АВС из вершины В проведена высота BD и биссектриса BL . Найдите площадь треугольника BLD , если известны длины сторон треугольника АВС : см; см; см.
5. В треугольнике АВС биссектриса угла С пересекает сторону АВ в точке D . Найдите площадь треугольника ADC , если , , .
6. В треугольнике АВС , , . Найдите отношение, в котором точка пересечения биссектрис делит биссектрису угла В .
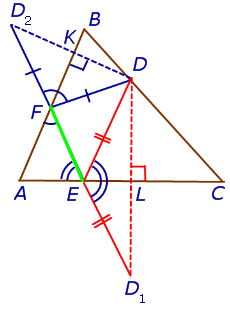
7. Основание равнобедренного треугольника равно 8, а боковая сторона 12. Найдите длину отрезка, соединяющего точки пересечения биссектрис углов при основании с боковыми сторонами треугольника.
Видео:Построение высоты в треугольникеСкачать

По теме: методические разработки, презентации и конспекты
Решение задач методом Ключевых ситуаций. Контрольная работа №1. 7-ой класс.» Плотность характиеризует вещество». «Архимедова сила»..
Дистанционный курс повышения квалификации «Как научиться решать задачи по физике (основная школа).Подготовка к ГИА». В школьном курсе огромное количество задач, которые можно сгруппировать вокруг неск.
Решение задач методом Ключевых ситуаций. Контрольная работа №1. 7-ой класс.» Плотность характиеризует вещество». «Архимедова сила»..
Дистанционный курс повышения квалификации «Как научиться решать задачи по физике (основная школа).Подготовка к ГИА». В школьном курсе огромное количество задач, которые можно сгруппировать вокруг неск.
Тема 24. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.Теория. Ключевые методы решения задач. Упражнения.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э.
Тема 26. МЕТОД КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ.Теория. Ключевые методы решения задач.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .
Тема 32. ТЕКСТОВЫЕ ЗАДАЧИ. Теория. Ключевые методы решения задач. Упражнения.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .
Презентация для подготовки к ГИА по теме «Ключевые задачи по геометрии»
Презентация для подготовки к ГИА по теме «Ключевые задачи по геометрии».
🎬 Видео
Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Задачи с подобными треугольникамиСкачать
Решение задач на тему "Подобные треугольники". 8 классСкачать

Задачи с подобными треугольниками 2Скачать

Уравнение прямой и треугольник. Задача про высотуСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Задача на подобие треугольников 1частьСкачать

Подобные треугольникиСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать