Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольника равны.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) В любой ромб можно вписать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Все высоты равностороннего треугольника равны» — верно, так как в равностороннем треугольнике все высоты равны между собой.
2) «Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу» — неверно, так как угол, вписанный в окружность, равен половине соответствующего центрального угла, опирающегося на ту же дугу.
3) «В любой ромб можно вписать окружность» — верно, так как суммы противоположных сторон ромба равны.
- Можно ли в окружность вписать ромб в окружность
- Можно ли в окружность вписать ромб в окружность
- Ромб. Формулы, признаки и свойства ромба
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- 📹 Видео
Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Можно ли в окружность вписать ромб в окружность
Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Можно ли в окружность вписать ромб в окружность
Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольника равны.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) В любой ромб можно вписать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Все высоты равностороннего треугольника равны» — верно, так как в равностороннем треугольнике все высоты равны между собой.
2) «Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу» — неверно, так как угол, вписанный в окружность, равен половине соответствующего центрального угла, опирающегося на ту же дугу.
3) «В любой ромб можно вписать окружность» — верно, так как суммы противоположных сторон ромба равны.
Видео:В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Ромб. Формулы, признаки и свойства ромба
 |  |
| Рис.1 | Рис.2 |
Видео:В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Признаки ромба
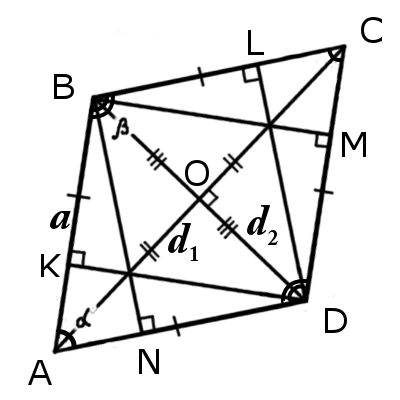
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:Если в четырёхугольник можно вписать окружностьСкачать

Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:Утверждения на ОГЭ - наш козырь на экзамене! / Готовимся к сентябрьской пересдаче ОГЭ! #3Скачать

Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:ОГЭ вариант-6 #13Скачать

Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать

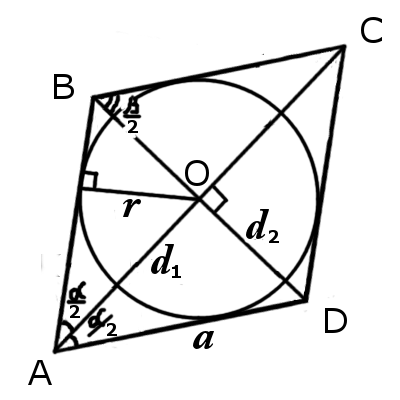
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Как сдать ОГЭ по математике на ТРОЙКУ? / Какие утверждения для фигур необходимо знать для сдачи ОГЭ?Скачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
📹 Видео
ОГЭ ЗАДАНИЕ 19 #математика #огэ #2023Скачать
ВСЕ ТИПЫ 19 задания на ОГЭ по математике 2024 | Дядя АртёмСкачать

Разбор задания 13 ОГЭ по математикеСкачать

ОГЭ 20🔴Скачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Геометрия Докажите, что если около ромба можно описать окружность, то этот ромб является квадратомСкачать

Euclidea - 2. Бета (Beta) - 2.10 - Окружность, вписанная в ромбСкачать

19 Задание ОГЭ по математике . Тренажер. Тема "Окружность"Скачать




