В кубе точка к середина ребра аа1 точка о центр авсд найдите вектор

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Ваш ответ

Видео:8 задание ЕГЭ по математике профильному.В кубе ABCDA1B1C1D1 точка K— середина ребра AA1,точка L—Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№362. Точка К — середина ребра ВС тетраэдра ABCD. Разложите вектор DK по векторамСкачать

В кубе точка к середина ребра аа1 точка о центр авсд найдите вектор

Задание 8. В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.

Так как ABCDA1B1C1D1 — куб, а точки K, L, M – середины соседних ребер (см. рисунок), то длины KL, KM, LM равны между собой как гипотенузы одинаковых прямоугольных треугольников. Раз в треугольнике KLM все стороны равны, то все углы в этом треугольнике по 60 градусов, следовательно, и угол MLK также 60 градусов.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Точка К – середина ребра АА 1 куба АВСDA 1 B 1 C 1 D 1. Найдите угол между прямыми А 1 В и СК. D А В С А1А1 D1D1 С1С1 В1В1 1 1 12 К Если в кубе не дано. — презентация

Презентация была опубликована 8 лет назад пользователемГеннадий Вельмукин

Похожие презентации

Видео:№167. В тетраэдре DABС все ребра равны, точка М— середина ребра АС. Докажите, что ∠DMBСкачать

Презентация на тему: » Точка К – середина ребра АА 1 куба АВСDA 1 B 1 C 1 D 1. Найдите угол между прямыми А 1 В и СК. D А В С А1А1 D1D1 С1С1 В1В1 1 1 12 К Если в кубе не дано.» — Транскрипт:

1 Точка К – середина ребра АА 1 куба АВСDA 1 B 1 C 1 D 1. Найдите угол между прямыми А 1 В и СК. D А В С А1А1 D1D1 С1С1 В1В К Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Заменим BA 1 на параллельную прямую CD 1. Угол между прямыми А 1 В и СК будет равен углу между CD 1 и СК способ

2 Точка К – середина ребра АА 1 куба АВСDA 1 B 1 C 1 D 1. Найдите угол между прямыми А 1 В и СК. D А В С А1А1 D1D1 С1С1 В1В К Применим теорему косинусов для треугольника CKD 1. Я хочу найти косинус угла KCD 1, значит, составляем теорему косинусов для стороны KD 1 :

Похожие презентации

Точка К – середина ребра АА 1 куба АВСDA 1 B 1 C 1 D 1. Найдите угол между прямыми А 1 В и СК. D АВ С А 1 А 1 D1D1 С 1 С 1 В 1 В 1 Если в кубе не дано.

11 A D C A1A1 B1B1 C1C1 D1D1 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Рассмотрев это трудоёмкое решение, метод координат.

AD C A1A1 B1B1 C1C1 D1D1 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Куб отлично вписывается в систему координат. х yz?

Прямая СС 1 является наклонной к плоскости ВС 1 D. Найдем проекцию СС 1 на плоскость ВС 1 D. D А В С А1А1 D1D1 С1С1 В кубе ABCDA 1 B 1 C 1 D 1 найдите.

BA B1B1 C1C1 D1D1 A1A1 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» 11 1 C На ребре СС 1 куба ABCDA 1 B 1 C 1 D 1 отмечена.

А1А1 В правильной треугольной призме ABCА 1 В 1 С 1, все ребра которой равны, найдите угол между прямыми КМ и ТЕ, где точка К – середина ребра АА 1, точка.

BA D B1B1 C1C1 D1D1 A1A1 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Куб отлично вписывается в систему координат. х yz?

В правильной шестиугольной призме АВСDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 1, точки G и H – середины ребер соответственно А 1 В 1 и В 1 С.

D C A B 1 E Заменим СL на параллельную прямую ME. Угол между прямыми DM и CL будет равен углу между DM и ME. Длина ребра правильного тетраэдра ABCD равна.

Сторона основания правильной треугольной призмы ABCA 1 B 1 C 1 равна 8. Высота этой призмы равна 6. Найти угол между прямыми CA 1 и АВ 1. C B1B1 A 8 60.

Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH высота данной пирамиды,

Заменим BC на параллельную хорду АM. Угол между прямыми АР и BС будет равен углу между АР и АМ. Применим теорему косинусов для треугольника МАР. Я хочу.

П-я 4 В А С1С1 В1В1 Основанием прямой призмы ABCA 1 B 1 C 1 является равнобедренный треугольник АВС, в котором СВ=СА=5, ВА=6. Высота призмы равна 24. Точка.

(1;1;0) В кубе ABCDA 1 B 1 C 1 D 1 точки E и K середины ребер соответственно A 1 B 1 и B 1 C 1. Найдите косинус угла между прямыми AE и BK. yzx D1D1D1D1.

BA D B1B1 C1C1 D1D1 A1A1 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Куб отлично вписывается в систему координат. х yz?

Р ЕШЕНИЕ ЗАДАНИЙ С 2. В ЕДИНИЧНОМ КУБЕ АВСDА 1 В 1 С 1 D 1 НАЙДИТЕ УГОЛ МЕЖДУ ПРЯМЫМИ АВ 1 И ВС 1. Решение: Введем систему координат, считая началом координат.

РАССТОЯНИЯ В ПРОСТРАНСТВЕ А. Азевич, г. Москва. Определение 1Расстоянием между точками называется длина отрезка, соединяющего эти точки.

Вычисление углов между прямыми и плоскостями 22.10.13 г.

T AB C M 1 K O1O1O1O1 В правильной четырехугольной пирамиде АВСMT со стороной основания а=4 и высотой ТО 1 = h =1. Найдите косинус угла между прямыми ОТ.

Дан куб ABCDA 1 B 1 C 1 D 1. Через О обозначим точку пересечения диагоналей грани ВВ 1 С 1 С куба. Найдите угол между прямыми АА 1 и ОD 1. B A1A1A1A1 B1B1B1B1.

📺 Видео

№365. Вне плоскости параллелограмма ABCD взята точка О. Точка M — середина АВ, а точка КСкачать

#104. Задание 8: кубСкачать

Геометрия Точка K середина ребра DC куба ABCDA1B1C1D1 Найдите косинус угла между прямыми B1C и C1KСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№326. На рисунке 104 изображен параллелепипед, точки М и К — середины ребер В1С1 и A1D1.Скачать

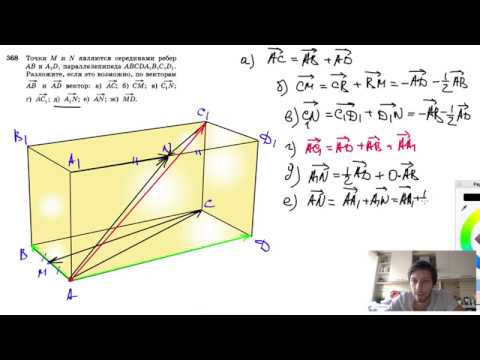
№368. Точки М и N являются серединами ребер АВ и A1D1 параллелепипеда ABCDA1B1C1D1.Скачать

Угол между векторами. 9 класс.Скачать

Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№356. Точки E и F - середины середины ребер AC и BD тетраэдра ABCD. Докажите, что 2FE = ВА + DCСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

№782. В параллелограмме ABCD точка Е — середина стороны AD, точка G — середина стороныСкачать

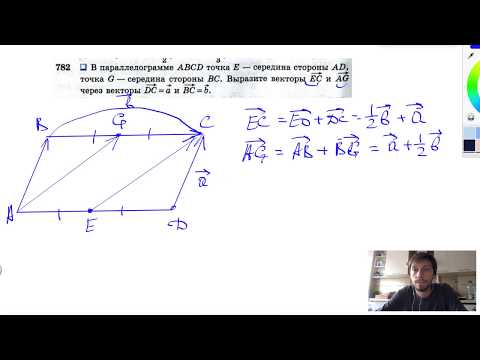
Точка E середина стороны AD параллелограмма ABCDСкачать