В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные b1c1

Геометрия | 5 — 9 классы

В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые параллельные прямой B1C1.

В кубе в плоскости ABCD B1C1||BC||AD.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Прямая а параллельна плоскость альфа?

Прямая а параллельна плоскость альфа.

Как через прямую а провести плоскость, параллельную плоскости альфа?

Видео:№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

«Прямая параллельная плоскости, параллельна всем прямым этой плоскости» Верно ли данное суждение?

«Прямая параллельная плоскости, параллельна всем прямым этой плоскости» Верно ли данное суждение?

Видео:№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

Прямая а параллельна одной из двух параллельных плоскостей?

Прямая а параллельна одной из двух параллельных плоскостей.

Докажите, что прямая а либо параллельна другой плоскости, либо лежит в ней.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1А и С1С , не лежащие в плоскости параллелограмма Докожите параллельность плоскостей А1АВ и С1СD?

Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1А и С1С , не лежащие в плоскости параллелограмма Докожите параллельность плоскостей А1АВ и С1СD.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Верно ли, что если плоскость параллельна одной из двух параллельных прямых, которые не лежат в этой плоскости, то она параллельна и другой прямой?

Верно ли, что если плоскость параллельна одной из двух параллельных прямых, которые не лежат в этой плоскости, то она параллельна и другой прямой?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба?

Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба.

Найдите угол между прямыми DC и m, если угол ABC = 134.

Видео:№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

1. Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями?

1. Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями.

Найдите АВ, если CD = 3 см.

2. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Две прямые параллельны одной плоскости ?

Две прямые параллельны одной плоскости .

Можно ли утверждать , что эти прямые параллельны?

Видео:№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

Прямая а параллельна плоскости альфа?

Прямая а параллельна плоскости альфа.

Существует ли на плоскости а прямая не параллельная прямой а?

Видео:В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

Верно ли следующее утверждение : «Прямая параллельна плоскости, если она параллельна прямой лежащей в этой плоскости?

Верно ли следующее утверждение : «Прямая параллельна плоскости, если она параллельна прямой лежащей в этой плоскости?

На этой странице сайта, в категории Геометрия размещен ответ на вопрос В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые параллельные прямой B1C1?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные b1c1

Вопрос по геометрии:

В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые параллельные прямой B1C1

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

В кубе в плоскости ABCD B1C1||BC||AD

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Геометрия Диагонали грани ABCD куба ABCDA1B1C1D1 пересекаются в точке O Найдите угол между прямымиСкачать

Подготовка к ЕГЭ

Разновидности стереометрических задач .

Просмотр содержимого документа
«Подготовка к ЕГЭ»

ПОДГОТОВКА К ЕГЭ. СТЕРЕОМЕТРИЧЕСКАЯ ЗАДАЧА(№14).

Работа учителя математики

Разновидности стереометрических задач.

• Расстояние от точки до прямой и до плоскости .
• Расстояние между прямыми и плоскостями .
• Угол между скрещивающимися прямыми .
• Угол между прямой и плоскостью .
• Угол между плоскостями .
• Задача на доказательство и вычисление .
• Сечения многогранников .
• Объёмы многогранников .
• Круглые тела: цилиндр, конус, шар.

Расстояние от точки до прямой.

• Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
• Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
• Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой .

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ,

где P и Q – середины соответственно

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки С до прямой ВД1.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД 1 .

1. ∆ВСД 1 – прямоугольный ( по теореме о трёх

перпендикулярах), ∠Д 1 СВ – прямой .

2. СН – высота ∆ВСД 1 , значит СВ – среднее

пропорциональное между ВН и ВД 1 , тогда

СН – расстояние от точки С до прямой ВД 1 , поэтому СН – высота треугольника ВСД 1 . СН = 2·S ∆ВСД 1 : ВД 1 .

∆ Д 1 СВ – прямоугольный, т.к. Д 1 С  СВ

по теореме о трёх перпендикулярах .

Расстояние от точки до плоскости .

• Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этого точки на плоскость.
• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

• В единичном кубе ABCDA₁B₁C₁D₁ найдите расстояние от точки C₁ до плоскости AB₁C.

• В правильной треугольной призме АВСА1В1С1–все рёбра равны 1.Найдите расстояние от точки А до плоскости (ВСА1)

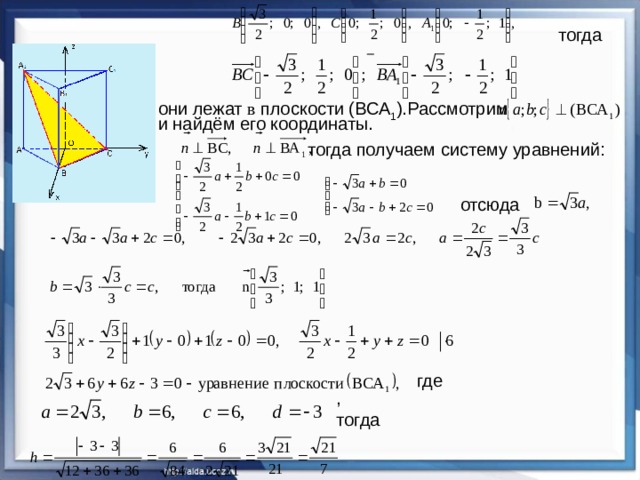
Дано: АВСА 1 В 1 С 1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА 1 )

Решение: h – расстояние от точки А до плоскости (ВСА 1 ),

поэтому h – высота пирамиды АВСА 1

с основанием ВСА 1 . h =

. Пусть основанием пирамиды будет ∆АВС,

тогда её высота – АА 1 .

∆ ВСА 1 – равнобедренный, А1К – его высота, тогда

За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:

они лежат в плоскости (ВСА 1 ).Рассмотрим

и найдём его координаты.

тогда получаем систему уравнений:

Расстояние между прямыми и плоскостями .

• Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр к двум скрещивающимся прямым существует и единственен.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найти: расстояние между прямыми АВ 1 и ВС 1 .

следовательно расстояние между скрещивающимися

прямыми ВС 1 и АВ 1 равно расстоянию между

соответствующими плоскостями. Диагональ СА 1

перпендикулярна этим плоскостям.

СА 1 ∩ (ВДС 1 ) = F;

CА 1 ∩ (АД 1 В 1 ) = Е.

EF – расстояние между ВС 1 и АВ 1 .

В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину отрезка АС, следовательно ОF – средняя линия треугольника АСЕ и, значит, ЕF = FC. Аналогично, О 1 Е – средняя линия треугольника А 1 С 1 F

Расстояние между скрещивающимися прямыми можно найти по формуле:

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ 1 и ВС 1 .

• SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1.Найдите расстояние между прямыми АS и ВС.

Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

Угол между прямой и плоскостью .

• Прямая и плоскость пересекаются , если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости .
• Прямая перпендикулярна к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.
• Проекцией точкиМна плоскость называется либо сама точка М , если М лежит в плоскости , либо точка пересечения плоскости и прямой, перпендикулярной к плоскости и проходящей через точку М , если точка М не лежит в плоскости .
• Проекцией прямойaна плоскость называют множество проекций всех точек прямой a на плоскость .
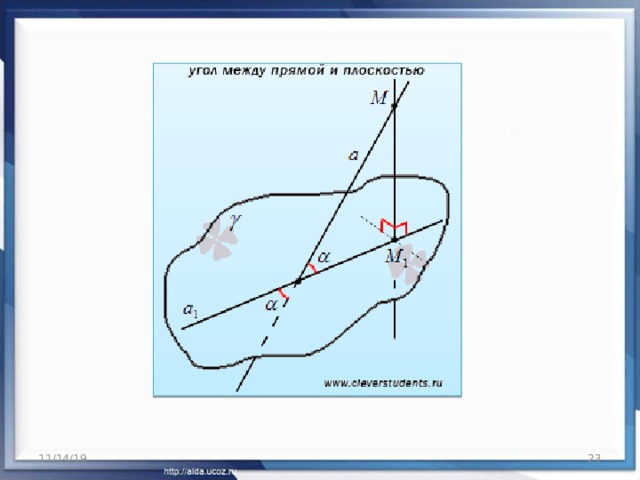
• Угол между прямой и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, — это угол между прямой и ее проекцией на эту плоскость.
• Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми : самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

На векторах построена пирамида. Найдите угол между прямой AD и плоскостью ABC .

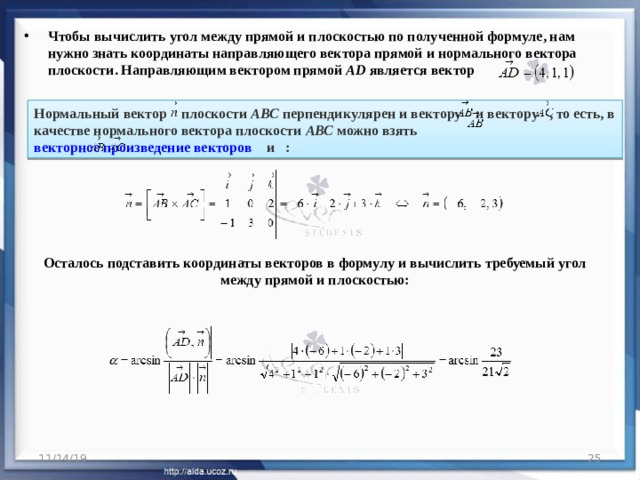
• На векторах построена пирамида. Найдите угол между прямойADи плоскостьюABC .

• Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямойADявляется вектор

Нормальный вектор плоскости АВС перпендикулярен и вектору и вектору , то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :

Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:

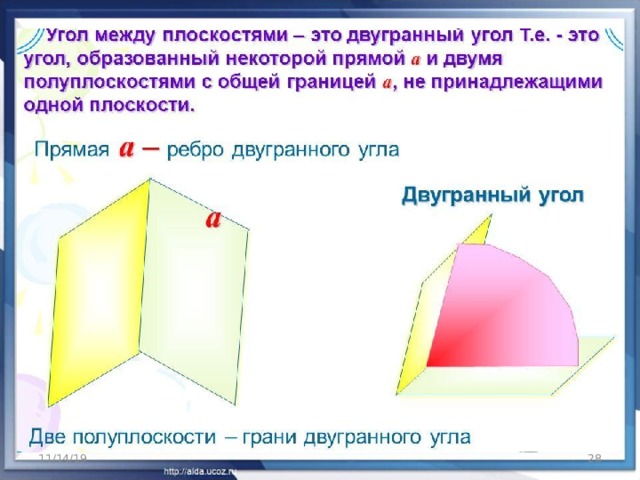
Угол между плоскостями .

Задача на доказательство и вычисление .

В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

В основании правильной треугольной призмы ABCA 1 B 1 C 1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A 1 C 1 .

а) Постройте сечение призмы плоскостью BAN .

б) Найдите периметр этого сечения.

См.сайт «Решу ЕГЭ»

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

В задачах используются в основном простейшие многогранники.

Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов. Метод вспомогательных сечений. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

• В правильной четырёхугольной пирамидеMABCDс вершинойMстороны основания равны 1, а боковые рёбра равны 2. ТочкаNпринадлежит ребруMC,причёмMN: NC = 2:1.Найдите площадь сечения пирамиды плоскостью, проходящей через точкиBиNпараллельно прямойAC.
• См . сайт «Решу ЕГЭ»

🎬 Видео

Готовимся к ЕГЭ. Стереометрия. Базовые задачи. Угол между прямыми. КубСкачать

№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Задание №443 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать