Пирог разрезают на неравные куски тремя прямыми разрезами. Какое наибольшее число кусков можно получить?
Сколько треугольников на рисунке?
Сколько треугольников на рисунке?
В каждую грань тетраэдра с ребром k вписана окружность. Найти отношение площади полной поверхности тетраэдра к сумме площадей образовавшихся кругов.
В каждую грань тетраэдра с ребром k вписана окружность. Найти разность площади полной поверхности тетраэдра и суммы площадей образовавшихся кругов.
Определите периметр треугольника, образованного прямыми, делящими ребра куба, выходящие из одной вершины в отношении (2:1) , считая от этой вершины, если ребро куба (9) см.
Определите площадь треугольника, образованного прямыми, делящими ребра куба, выходящие из одной вершины в отношении (2:1) , считая от этой вершины, если ребро куба равно (9) см.
Определите площадь треугольника, образованного серединами ребер куба, выходящих из одной вершины, если ребро куба равно (8) см.
Определите периметр треугольника, образованного серединами ребер куба, выходящих из одной вершины, если ребро куба равно (8) см.
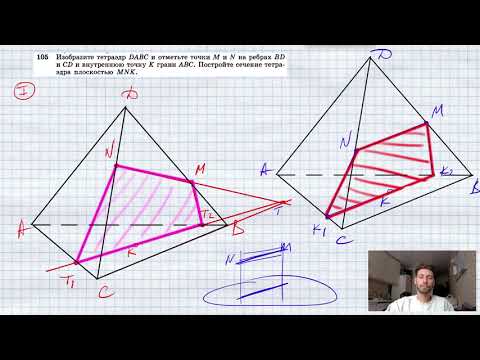
Видео:№105. Изобразите тетраэдр DABС и отметьте точки М и N на ребрах BD и CD и внутреннюю точку К грани AСкачать
Тетраэдр.
Тетраэдр — это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Видео:Самый сложный пример 5 задание проф. ЕГЭ (часть III)Скачать

Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Видео:Как достроить равногранный тетраэдр и найти радиус описанной сферыСкачать

Типы тетраэдров.
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр — это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
— Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
— Соразмерный тетраэдр, бивысоты у него одинаковы.
— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Формулы для определения элементов тетраэдра.
Высота тетраэдра:
где h — высота тетраэдра, a — ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
где V — объем тетраэдра, a — ребро тетраэдра.
Основные формулы для правильного тетраэдра:
Где S — Площадь поверхности правильного тетраэдра;
h — высота, опущенная на основание;
r — радиус вписанной в тетраэдр окружности;
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Правильные многогранники
Правильными называют выпуклые многогранники, все грани которых представляют собой одинаковые правильные многоугольники, и в каждой вершине сходится одинаковое количество граней. Такие многогранники называют также платоновыми телами.
Существует всего пять правильных многогранников:
Тип правильного многогранника
Число сторон у грани
Число рёбер, примыкающих к вершине
Общее число вершин
Общее число рёбер
Общее число граней


Гексаэдр или куб



Название каждого многогранника происходит от греческого названия количества его граней и слова «грань».
Тетраэдр (греч. фефсбедспн — четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
- · равногранный тетраэдр, у которого все грани — равные между собой треугольники;
- · ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке;
- · прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой;
- · правильный тетраэдр, у которого все грани — равносторонние треугольники;
- · каркасный тетраэдр — тетраэдр, отвечающий любому из условий[1]:
- · Существует сфера, касающаяся всех ребер.
- · Суммы длин скрещивающихся ребер равны.
- · Суммы двугранных углов при противоположных ребрах равны.
- · Окружности, вписанные в грани, попарно касаются.
- · Все четырехугольники, получающиеся на развертке тетраэдра, — описанные.
- · Перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
- · соразмерный тетраэдр, все бивысоты которого равны;
- · инцентрический тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
- · Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
- · В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
- · В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
- · Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
- · В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле
многогранник икосаэдр октаэдр додекаэдр
где d — диагональ, а — ребро куба.
Октаэдр (греч. пкфЬедспн, от греч. пкфю, «восемь» и греч. Эдсб — «основание») — один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.
Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Если длина ребра октаэдра равна а, то площадь его полной поверхности (S) и объём октаэдра (V) вычисляются по формулам:
Радиус сферы, описанной вокруг октаэдра, равен:
радиус вписанной в октаэдр сферы может быть вычислен по формуле:
Правильный октаэдр имеет симметрию Oh, совпадающую с симметрией куба.
Октаэдр имеет одну звездчатую форму. Октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название «stella octangula Кеплера».
По сути она является соединением двух тетраэдров
Додекаэдр (от греч. дюдекб — двенадцать и едспн — грань), двенадцатигранник — правильный многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°.
Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр (звёздчатый большой додекаэдр, завершающая форма). Первые две из них были открыты Кеплером (1619), третья — Пуансо (1809). В отличие от октаэдра любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник.

Все 3 звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников.
У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани — пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3. Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра. У каждой вершины соединяются три грани.
Если за длину ребра принять a, то площадь поверхности додекаэдра:
Радиус описанной сферы:
Радиус вписанной сферы:
Элементы симметрии додекаэдра:
· Додекаэдр имеет центр симметрии и 15 осей симметрии.
Каждая из осей проходит через середины противолежащих параллельных ребер.
· Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.
Икосаэдр (от греч. ейкпуЬт — двадцать; -едспн — грань, лицо, основание) — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Площадь S, объём V икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:
радиус вписанной сферы:
радиус описанной сферы:
- · Икосаэдр можно вписать в куб, при этом, шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
- · В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
- · Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
- · В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
- · Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12?5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12?5=90.
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией. Одна из этих звёздчатых форм (20-я, мод. 41 по Веннинджеру), называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
Среди звёздчатых форм также имеются: соединение пяти октаэдров, соединение пяти тетраэдров, соединение десяти тетраэдров.
🔥 Видео
Сечение Пирамиды Плоскостью Параллельной боковому ребруСкачать

11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

10 класс, 33 урок, Правильная пирамидаСкачать

Вписанная окружностьСкачать

✓ Секретная формула объема | Стереометрия | Физтех-2014. Математика | Борис ТрушинСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10 класс, 12 урок, ТетраэдрСкачать

Боковые ребра треугольной пирамиды взаимно перпендикулярныСкачать

№69. Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SBСкачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Объём тетраэдра 19 Найдите объём многогранника, вершинами которого являются середины рёберСкачать

Решаем стереометрию 13 задание подряд | ЕГЭ математика 2023 | Часть 2Скачать

№258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.Скачать

10кл.Егэ.Во сколько раз увеличится площадь поверхности правильного тетраэдра, если всеСкачать

















