Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Значения тангенса и котангенса на тригонометрическом круге
- Свойства синуса, косинуса, тангенса и котангенса
- Знаки тригонометрических функций по четвертям
- Свойство периодичности
- Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
- 🔍 Видео
Видео:Знаки синуса, косинуса, тангенса ЛекцияСкачать
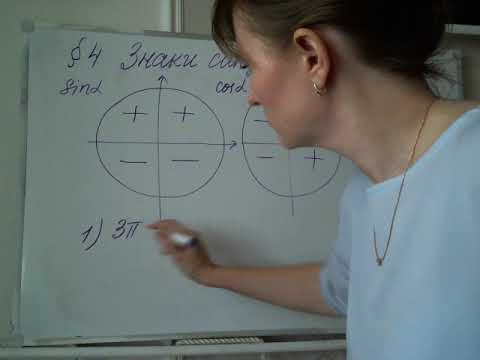
Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Тригонометрическая окружность. Как выучить?Скачать  Значения тангенса и котангенса на тригонометрическом кругеВ прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов. Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня. Где же на тригонометрическом круге оси тангенсов и котангенсов? Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0). Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1). На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что
Собственно, картинка за себя сама говорит. Если не очень все же понятно, разберем примеры: Пример 1. Вычислить Находим на круге Ответ: Пример 2. Вычислить Находим на круге Ответ: не существует Пример 3. Вычислить
Находим на круге точку Так значит, Ответ: Пример 4. Вычислить
Поэтому от точки Выходим на ось котангенсов, получаем, что Ответ: Пример 5. Вычислить Находим на круге Ответ:
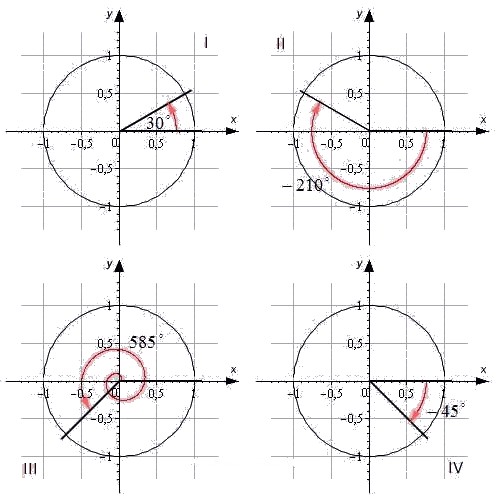
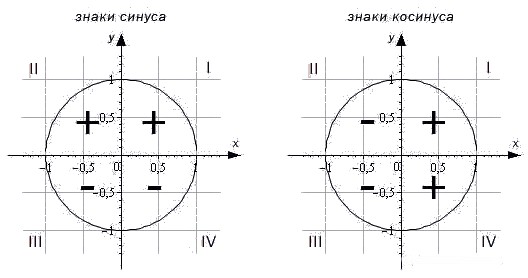
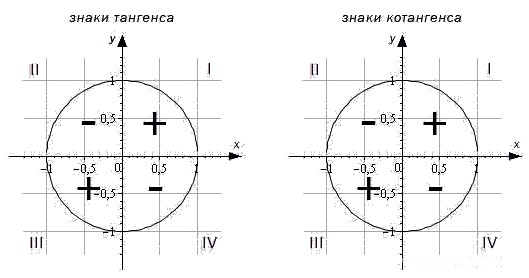
Чтобы не потерять страничку, вы можете сохранить ее у себя: Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать  Свойства синуса, косинуса, тангенса и котангенсаВ этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса. Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α . Видео:10 класс, 11 урок, Числовая окружностьСкачать  Знаки тригонометрических функций по четвертямЧасто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое? Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 ( 1 , 0 ) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 ( x , y ) . В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти. При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях. Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол. Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 ( x , y ) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна. Косинус — это абсцисса точки A 1 ( x , y ) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
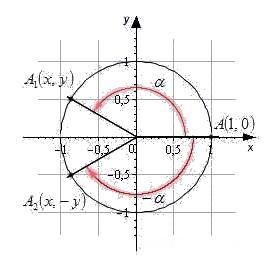
Видео:Найти знак тригонометрической функции (bezbotvy)Скачать 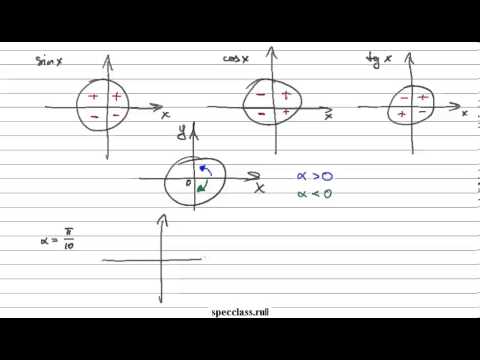 Свойство периодичностиСвойство периодичности — одно из самых очевидных свойств тригонометрических функций. При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными. Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса. Математически данное свойство записывается так: sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов. sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5 t g ( — 689 ° ) = t g ( 31 ° + 360 ° · ( — 2 ) ) = t g 31 ° t g ( — 689 ° ) = t g ( — 329 ° + 360 ° · ( — 1 ) ) = t g ( — 329 ° ) Видео:Знаки тригонометрических функций. 9 класс.Скачать 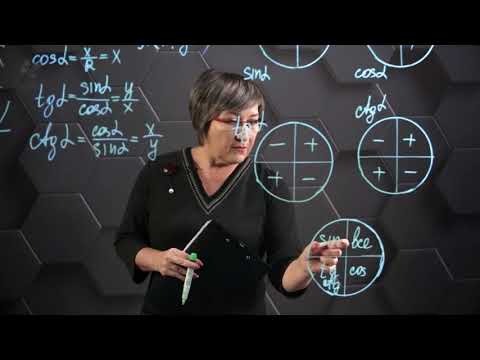 Свойства синусов, косинусов, тангенсов и котангенсов противоположных угловВновь обратимся к единичной окружности.
Точка A 1 ( x , y ) — результат поворота начальной точки A 0 ( 1 , 0 ) вокруг центра окружности на угол α . Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α . Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты ( x , y ) , а вторая — ( x , — y ) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем: sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов. Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α Согласно этому свойству, справедливы равенства sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 ° Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций. 🔍 ВидеоПериод тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать  Алгебра 10 класс (Урок№31 - Знаки синуса, косинуса и тангенса.)Скачать  Как искать точки на тригонометрической окружности.Скачать  Таблица значений тригонометрических функций - как её запомнить!!!Скачать  ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать  ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Синус косинус тангенс котангенс числа. В какой четверти находится угол поворота. Тригонометрия 8-11Скачать  Период тригонометрических функций в радианах с числом Пи. В какой четверти находится угол поворота.Скачать  Тригонометрическая окружность tg x и ctg xСкачать  🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать  Вычисление значений тригонометрических функцийСкачать  Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Синус, косинус произвольного угла. 9 класс.Скачать  |
Почему так?
и 
. Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что 
. Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
(это та же точка, что и 
) и от нее по часовой стрелке (знак минус!) откладываем 
(
). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как 
. Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение 
.
(именно там будет 
) откладываем против часовой стрелки 
.
. Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что 
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
