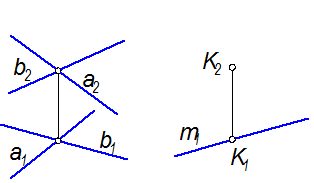
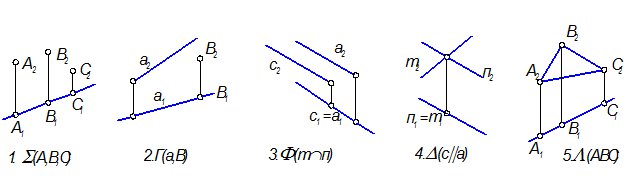В каком случае через точку k проведена горизонтально проецирующая плоскость w параллельная прямой а (5 видео)

Прямая, параллельная плоскости

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

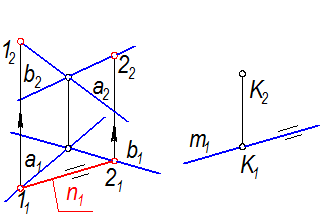
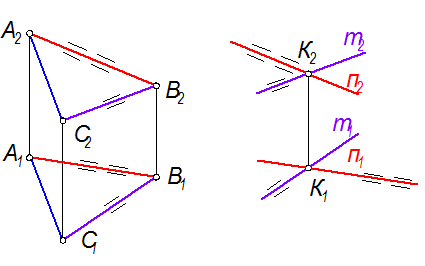
Задача: Через точку К(К₂,К₁) провести прямую m(m₁), параллельную плоскости S(aÇb)

Алгоритм

1. В плоскости S (рис. 2-28) проведём прямую n, параллельную m. Для этого сначала проведём 1₁2₁ || m₁, затем найдём 1₂2₂ в плоскости. Это будет n₂

3. Согласно пятому свойству параллельного проецирования прямая m параллельна прямой n, но nÌ S, следовательно, m || S

Взаимная параллельность плоскостей

Построение двух взаимно параллельных плоскостей основано на известном положении, что две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

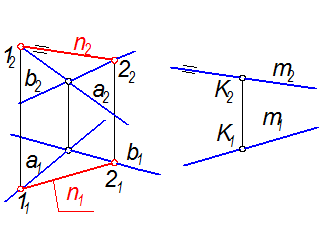
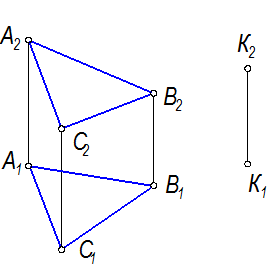
Задача: Через точку К(К₁К₂) (рис. 2-31.а) провести плоскость D, параллельную плоскости Г(АВС). Плоскость D задать пересекающимися прямыми.

Алгоритм:

1. Плоскость D зададим прямыми m Ç n = K (рис. 2-31).

4. Таким образом, плоскости S(АВС) и D(m Ç n) параллельны.

Как вы думаете?

1. Сколько решений может иметь задача, представленная на рис. 2-30?

2. Чем можно ещё задать плоскость D, кроме решения, приведённого на рис. 2-31?

3. Сколько ответов может быть у задачи, представленной на рис. 2-29? Почему?

Выводы:

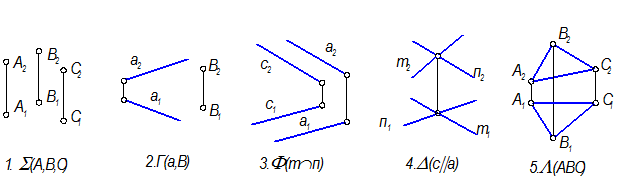
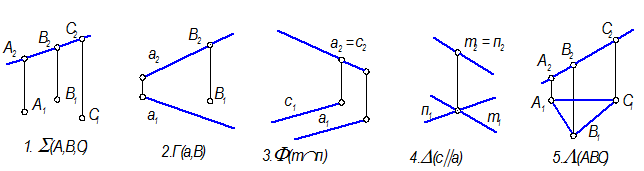
1. В общем случае плоскость определяют три точки.

2. Общий признак плоскостей частного положения — одна из проекций вырождается в прямую линию.

3. Точку в плоскости находят по принадлежности какой-нибудь прямой этой плоскости.

4. В любой плоскости можно построить прямые уровня и линии наибольшего наклона плоскости к каждой из плоскостей проекций.

5. Через точку, лежащую вне плоскости, можно провести сколько угодно прямых, параллельных данной плоскости, но только одну плоскость, параллельную заданной.

Справочный материал

Примеры изображения плоскостей общего и частного положения, заданные геометрическими фигурами

Плоскости общего положения

Графический признак плоскости общего положения: ни одна из проекций не есть прямая линия.

Горизонтально проецирующие плоскости

Плоскости горизонтальные проекции которых есть прямые линии не || и не ^ Л.С.(линиям связи).

Фронтально проецирующие плоскости

Плоскости, фронтальные проекции которых есть прямые линии не || и не ^ Л.С.

Горизонтальные плоскости уровня

Плоскости, фронтальные проекции которых есть прямые линии ^ Л.С.

Содержание

Решение: Через прямую проведем горизонтально проецирующую плоскость Г(рис. 4а) и эпюре обозначим совпадение горизонтальных проекций прямой и плоскости: ι≡Г
Главная > Решение
Лекции по начертательной геометрии (стр. 5 )
📽️ Видео

Видео:Провести горизонтальную прямую через точку и пересекающую заданный отрезок. Начертательная геометрияСкачать

Решение: Через прямую проведем горизонтально проецирующую плоскость Г(рис. 4а) и эпюре обозначим совпадение горизонтальных проекций прямой и плоскости: ι≡Г

Главная > Решение

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Взаимное положение прямой и плоскости

Быть параллельной плоскости;

Пересекаться с плоскостью.

Прямая принадлежит плоскости, если она проходит хотя бы через две точки, лежащие в этой плоскости.( рис.1)

2.Прямая параллельна плоскости, если она параллельна какой –либо прямой, лежащей в этой плоскости (рис.2)

3. Прямая пересекается с плоскостью ( 1 позиционная задача )

Построить точку пересечения прямой ι с плоскостью Σ(АВС) (рис.4)

Алгоритм решения включает три основных этапа:

1.Через заданную прямую проводят вспомогательную проецирующую плоскость.

2.Строят линию пересечения заданной прямой и построенной линии пересечения плоскостей, то есть искомую точку пересечения прямой с плоскостью.

Через прямую проведем горизонтально – проецирующую плоскость Г(рис.4а)

и эпюре обозначим совпадение горизонтальных проекций прямой и плоскости: ι≡Г

Из курса геометрии известно, две плоскости пересекаются по прямой линии.

Пусть 1-2 – линия пересечения плоскостей Г и Σ.Точки 1 и 2 – это точки пересечения прямых АВ и АС плоскости Σ с плоскостью Г (рис. 4а)

АВГ =1 ; АСГ =2,на эпюре: А1В1Г1 =11; А1С1 Г1 =21, по

линиям связи находим: 12 А2В2, 22 А2 С2

Прямые 1-2 и ι , расположенные в одной плоскости Г, являются горизонтально конкурирующими прямыми:

Обратимся к фронтальным проекциям прямых:ι212 – 22 = К2, К(К1 ; К2 ) –искомая точка пересечения прямой ι с плоскостью Σ.

Для определения видимости на плоскости П1 нужно сравнить высоты двух горизонтально конкурирующих точек 2 и 3 : Z3 >Z2 ,следовательно , точка 3 видима на П1 . Для определения видимости на плоскости П2 нужно сравнить ординаты двух фронтально конкурирующих точек, например,4 и 5: y5>y4 , следовательно, точка 5 на П2 видимая.(Рис.4б)

ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ

Две плоскости могут быть взаимно параллельны или пересекаться.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости взаимно параллельны (рис.5).

Две плоскости пересекаются по прямой линии Для построения линии пересечения двух плоскостей необходимо найти две точки, общие для данных плоскостей. Рассмотрим случай ,когда одна из плоскостей общего, а другая частного положения(рис.6).

Дано: Σ (АВС) и Г(Г2 )- плоскость уровня. Построить линию пересечения плоскостей 1-2.

1.АВ Σ ; АВГ =1;

2.ВСΣ ; ВСГ =2;

3. ΣГ = 1-2-линия пересечения плоскостей.

Фронтальная проекция линии пересечения 12-22║х, следовательно, 1-2 является горизонталью плоскости Σ.

В том случае, когда обе плоскости общего положения и проекции определителей плоскостей на эпюре не

пересекаются в пределах чертежа, применяют метод

вспомогательных секущих плоскостей-посредников, которыми являются плоскости частного положения.

Рассмотрим пример (рис.7).

Пусть даны две плоскости Σ (ι ║m) и Г (пр).Построить линию пересечения: ГΣ =1-2.

В качестве посредника используем плоскость.

Λ Σ =a; ΛΣ=b; ab= 1.

Точка 1 принадлежит как плоскости Г , так и плоскости Σ , т.е. она

принадлежит линии их пересечения. Чтобы построить точку 2, проведем плоскость Λ´ и будем иметь:

Λ´ Σ = с; Λ´Г=d; сd=2.

Итак,1-2 – линия пересечения плоскостей Σ и Г.

На рис. 8 показано решение задачи на эпюре.

1. Λ Σ (ι ║m) =a; Λ Г ( пp) = b; ab= 1

2. Λ´ Σ =с; Λ Г =d; сd = 2; 1 – 2 =ГΣ.

Рассмотрим еще один пример (рис. 9)

Даны две треугольные пластины АВС и DЕF .Чтобы построить линию пересечения плоскостей 1-2 достаточно найти точки пересечения сторон DF и FЕ плоскости DЕF с плоскостью АВС.

1.DF; АВС = МN ; М N DF =1;

2.ЕF R ; RABC=KL; К LEF=2;

3.1-2 =АВСDЕF

Видимость проекций пластины DЕF определена методом конкурирующих точек.

Видео:Лекция 1. Классификация прямых линий.Скачать

Лекции по начертательной геометрии (стр. 5 )

В каком случае через точку k проведена горизонтально проецирующая плоскость w параллельная прямой а

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

Теперь по чертежу определим, какая прямая задана. Так как отрезок АВ не проецировался на плоскости проекций в точку (см. п. 3.1.1), следовательно, это не проецирующая прямая. Так как проекция А1В1 или проекция А2В2 не параллельны оси проекций Х (см. п. 3.1.2), то это не прямая уровня. Следовательно, построенный отрезок является прямой общего положения (см. п. 3.1.3).

Задача 3.2. Через точку С(25, 15, 5) провести горизонтально-проецирующую прямую m длиной 20мм.

Решение. По координатам строим комплексный чертеж точки С, т. е. С1 и С2. Согласно п.3.1.1 и рис.3.1б горизонтальная проекция m1 этой прямой представляет собой точку, а т. к. прямая m проходит через точку С, то их горизонтальные проекции совпадут, т. е. m1 º С1. Поскольку на П2 проекция m2 прямой m изображается вертикально, а ее длина равна длине прямой, то от С2 откладываем отрезок m2 равный 20мм. Полученное изображение является комплексным чертежом прямой m (рис.3.20).

Задача 3.3. Построить комплексный чертеж отрезка прямой MN, если заданы координаты M(15, 5, 15), N( ?, 5,10). Длина отрезка êMN ê= 20мм. Как называется эта прямая?

Решение. Рассмотрим внимательно координаты точек M и N. Для точки N координата Х не известна. Однако можно заметить, что координаты Y для точек M и N одинаковы, а координаты Z различные. Следовательно, горизонтальная проекция M1N1 отрезка параллельна оси проекций Х. Такое положение может быть только в одном случае, когда эта прямая — фронталь (см. рис.3.5б). Тогда фронтальная проекция M2N2 проецируется в натуральную величину, равную 20мм (см. п. 3.1.2б). Поскольку известно, что проекция N2 по координате Z находится на высоте 10 мм, а расстояние от M2 до N2 составляет 20мм, то из точки М2 циркулем радиусом 20мм проводим дугу. Там, где дуга пересечет координатную линию, соответствующую Z=10мм, строим проекцию N2 точки N.

Проекцию N1 строим по линии связи на координате YN=5мм. Соответствующие точки соединяем отрезками прямых линий. Полученное изображение является комплексным чертежом фронтали (рис. 3.21).

Задача 3.4. Определить относительное положение точек А, В, С, D и прямой m (рис. 3.22).

Решение. Для решения этой задачи воспользуемся рекомендациями п.3.2.

а). Т. к. горизонтальная проекция А1 ниже проекции m1, следовательно точка А находится перед прямой m.

Т. к. проекция А2 ниже проекции m2, значит точка А расположена ниже прямой m.

б). Точка В не лежит на прямой m, т. к. проекция В2 выше проекции m2. Следовательно точка В находится над прямой m.

в). У точки С обе проекции лежат на одноименных проекциях прямой, т. е. С1Ì m1, а С2Ì m2, тогда СÌ m.

г). Точка D не лежит на прямой m, т. к. проекция D1 не лежит на проекции m1 прямой, а находится за ней. Поэтому точка D расположена за прямой m.

Задача 3.5. Определить расположение прямых b, d, f относительно плоскостей проекций П1 и П2 и взаимное расположение этих прямых (рис.3.23).

Решение. а). Вначале выполним первое условие.

Из п.3.1 известно, что прямые относительно плоскостей проекций могут быть проецирующими, уровня или общего положения.

Из рис.3.23 видно, что горизонтальная проекция d1 прямой d представляет собой точку, а ее фронтальная проекция d2 – вертикальную прямую. Сравнив с рис.3.1б, можно сделать вывод, что прямая d-это горизонтально — проецирующая прямая.

У прямой f горизонтальная проекция f1 представляет собой прямую параллельную оси проекций Х, а фронтальная проекция f2 –наклонную прямую. Сравнив с рис. 3.5б, можно сделать вывод, что прямая f— это фронтальная прямая уровня, или фронталь.

Ни одна из проекций b1 или b2 прямой b не являются точкой и не параллельны оси проекций, следовательно, это прямая общего положения.

б). Согласно п.3.4 прямые линии могут быть параллельны между собой, пересекаться или быть скрещивающимися прямыми.

Вначале рассмотрим положение прямых f и b. Горизонтальные проекции и фронтальные проекции этих прямых имеют точки пересечения и согласно рис. 3.23 эти точки пересечения лежат на одной линии связи, следовательно, прямые f и b пересекаются.

По расположению проекций прямых d и f видно, что d1 лежит на проекции f1 в виде точки, а фронтальные проекции их также пересекаются на одной линии связи, следовательно, прямая d проходит через прямую f, а, значит, пересекает ее.

Проекции прямых b и d не параллельны и не имеют общих точек пересечения, следовательно, прямые b и d являются скрещивающимися прямыми.

Ответ: f ∩b, d ∩f, b d.

Задача 3.6. Определить взаимное расположение отрезков прямых АВ и СD (рис.3.24а).

Рис. 3.24а Рис.3.24б

Решение. На основании рис. 3.24а можно сделать вывод, что отрезки прямых АВ и СD параллельны между собой. Однако это впечатление может быть обманчиво. Проверим это, выполнив профильную проекцию отрезков прямых (рис. 3.24б). Зная из чертежа координаты Х, Y,Z точек А, В,С, D, построим проекции этих точек на профильной плоскости проекций (см. задачу 2.3 раздела 2). Соединив полученные проекции точек отрезками прямых линий А3В3 и С3D3, видим, что эти отрезки не параллельны, а, следовательно, прямые АВ и СD являются скрещивающимися прямыми.

Решение. Чтобы построить какую-либо прямую, необходимо, чтобы она проходила минимум через две точки. Такую прямую можно провести, начиная построение на горизонтальной проекции с соблюдением условий задачи. Так горизонтальную проекцию t1 необходимо провести через проекцию А1, т. к. по условию прямая t проходит через точку А, в то же время t1 проходит через проекцию d1 горизонтально — проецирующей прямой d, поскольку должно выполниться условие задачи, что t Ç d. Горизонтальную проекцию точки пересечения обозначим D1(d1 º D1), а точку пересечения t1 с проекцией b1 обозначим В1.

Теперь построим проекцию t2 прямой t. Вначале из В1 по линии связи построим фронтальную проекцию В2 точки пересечения линий t и b. Через точки А2 и В2 построим прямую t2 до пересечения с d2, где отметим точку D2 (рис.3.25б). Задача решена.

Задача 3.8. Даны проекции прямых линий m и n (рис.3.26а). Построить фронталь, пересекающую обе прямые и расположенную на расстоянии 10мм от плоскости проекций П2.

Рис. 3.26а Рис. 3.26б

Решение. Согласно п. 3.1.2 фронталь относится к прямым уровня, т. е. она параллельна фронтальной плоскости проекций П2. Особенностью этой прямой линии заключается в том, что ее горизонтальная проекция параллельна оси проекций Х (см. рис.3.5б). Так как фронталь расположена от П2 на расстоянии 10мм, то фронталь надо начинать строить с ее горизонтальной проекции f1, которую следует провести на расстоянии 10мм от оси проекций Х параллельно Х (рис.3.26б). Так как по условию фронталь пересекает прямые m и n, строим точки пересечения f1 с прямыми m1 и n1. Получаем соответственно М1 и N1. Теперь от этих проекций по линиям связи строим фронтальные проекции М2 и N2 точек пересечения фронтали с заданными прямыми соответственно на прямых m2 и n2. Точки М2 и N2 соединяем прямой линией, которая является фронтальной проекцией f2 фронтали. Задача решена (рис. 3.26б).