Дано a1a2 a1a3 10 a2a3 12 o центр окружности вписанной

— выработать навыки решения типовых задач на применение формул объемов пирамиды и усеченной пирамиды.

I. Проверка домашнего задания

Задача № 697. Дано: АВСА1В1С1 — правильная усеченная пирамида. АВ = а, А1В1 = 0,5а. ММ1 ⊥ ВС, ММ1 = а (рис. 1).

1) Рассмотрим ΔАВС, найдем

2) ΔА1В1С1, найдем A1М1 (A1М1 ⊥ В1С1).

3)

4) Рассмотрим прямоугольную трапецию ОО1М1М (рис 1 a)):

Из ΔКМ1М: ∠K = 90°, по теореме Пифагора.

(Ответ: )

II. Решение задач

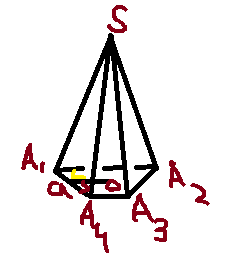
1. Дано: A1A2A3A4 — трапеция, А1А4 = А3А2, О — центр окружности, вписанной в трапецию SO ⊥ (А1А2А3), А1А4 = а1 (рис. 2).

1) Проведем A4C ⊥ A1A2. Рассмотрим ΔА1СA4. ∠С = 90°, А1А4 = а, тогда А1С = h = asinα,

2) H = SO = OBtgβ = 0,5a sinαtgβ.

3) Рассмотрим равнобедренную трапецию A1A2A3A4, найдем ее площадь. Н = А4С = asinα. Пусть CD = x, тогда (рис. 3) А1С = acosα, подставим в формулу, С одной стороны, площадь многоугольника можно найти через периметр и радиус вписанной окружности. тогда Уравняем правые части, После упрощения получим х = а — acosα. Итак, площадь основания равна

4) (Ответ: )

III. Проверочная самостоятельная работа (разноуровневая) (см. приложение.

Вариант А1 192 см3. Вариант Б1 343 см3. Вариант B1

Вариант A2 360 см3. Вариант Б2 320 см3. Вариант B2

Решение проверочной самостоятельной работы

1) AS = BS = CS = DS, значит, АО = ВО = СО = DO.

192 см3. (Ответ: 192 см3.)

360 см3. (Ответ: 360 см3.)

1) ∠SMO = 45°, точка О — центр вписанной в основание окружности, ОМ = r, ОМ ⊥ ВС.

2) формула Герона. с др. стороны

3) ΔSOM — равнобедренный, SO = ОМ = 7 см.

4) (Ответ: 343 см3..

1) Так как ∠ASO = ∠BSO = ∠CSO = 45°, то ∠SAO = ∠SBO = ∠SCO; тогда AО = OB = ОС = R.

2) ОА = OB, точка О — центр окружности, описанной около основания.

1) Пусть BC = а,

2) с другой стороны Приравниваем,

(Ответ: )

2) Составим равенство из формул для вычисления площадей треугольника.

3)

(Ответ: ).

Обменяться вариантами самостоятельной работы.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Задача 8700 Дано: А1А2А3А4 – трапеция А1А4=А2А3 =.

Условие

Дано:
А1А2А3А4 – трапеция
А1А4=А2А3 = а
О –центр окружности, вписанной в А1А2А3А4
ОL–радиус описанной окружности
Найти:
Vпирамиды – ?

Решение

Рассмотрим основание пирамиды. Первым делом нам надо найти площадь основания. Высота трапеции h=2r, ребро равно a. Синус угла между боковой стороной и основанием sinальфа = 2r/a

По формуле 4r^2/sinальфа находим площадь основания

C имеющимися данными невозможно найти высоту пирамиды, а значит и объем пирамиды тоже. А так получилось бы

V = (1/3) * (4r^2/sinальфа) * H, где H высота пирамиды

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

ПОЖАЛУЙСТА СРОЧНО дано а1а2а3а4 ромб а1а3 24 а2а4 10 найти sполн?

Геометрия | 5 — 9 классы

ПОЖАЛУЙСТА СРОЧНО дано а1а2а3а4 ромб а1а3 24 а2а4 10 найти sполн.

S(полн) = 2 S (осн) + S ( бок)

S (осн) = 1 / 2·A1A3·A2A4 = 1 / 2·24·10 = 120

Р(осн) = 4 а , где а — сторона основания а = А4А3

ИзΔ А4А3А3′ ⇒ равнобедренный ⇒ А4А3 = А3А3′ ⇒ a = H

ИЗΔ А4ОА3 , где О = А1А3∩ А2А4 найдём А4А3 по т.

ОА3 = 24 / 2 = 12 , ОА4 = 10 / 2 = 5

А3А4 = √12² + 5² = √144 + 25 = √ 169 = 13 ⇒ Н = а = 13

S (бок) = 4·а·Н = 4·13·13 = 4·169 = 676

S(полн) = 2S(осн) + S(бок) = 2·120 + 676 = 916.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Дано : ABCD — ромб Найти угол с?

Дано : ABCD — ромб Найти угол с.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

В прямоугольном параллелепипеде abcda1b1c1d1 лежит ромб abcd со стороной равной а и угол bad равен 60 градусов?

В прямоугольном параллелепипеде abcda1b1c1d1 лежит ромб abcd со стороной равной а и угол bad равен 60 градусов.

Видео:№207. В треугольнике ABC дано: АВ = ВС = 13 см, AС = 10 см. Точка М удалена от прямых АВ, ВС и АС наСкачать

Дано : Правильная призма ABCDEM AC = 6CM MA = 10CM НАЙТИ : SБОК?

Дано : Правильная призма ABCDEM AC = 6CM MA = 10CM НАЙТИ : SБОК.

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Дано ABCD ромб найти BF — ?

Дано ABCD ромб найти BF — ?

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Помогите пожалуйста через дано решить?

Помогите пожалуйста через дано решить!

Найти углы ромба, если один из них на 40 градусов больше другого.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Дан ромб, все стороны равны, найти углы ромба?

Дан ромб, все стороны равны, найти углы ромба.

Видео:ОГЭ 2021| Математика | Геометрическая задача повышенной сложности. Окружности. Урок 8Скачать

Помогите с задачей по геометрии) Дано : Дан цилиндр?

Помогите с задачей по геометрии) Дано : Дан цилиндр.

R = корень из 3 см h = 7 см.

Найти : Sбоковую и Sполную.

Видео:§ 13 № 1- 55 - Геометрия 7-9 класс ПогореловСкачать

Дан ABCD — ромб, AC = 20см ; BD = 7см?

Дан ABCD — ромб, AC = 20см ; BD = 7см.

Найти площадь ромба.

Видео:№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать

ПОМОГИТЕ ПОЖАЛУЙСТА?

Дано : ABCD — ромб.

Найти : угол CBE.

Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

ПОЖАЛУЙСТА РЕШИТЕ СРОЧНО НАДО АААА?

ПОЖАЛУЙСТА РЕШИТЕ СРОЧНО НАДО АААА.

Вопрос ПОЖАЛУЙСТА СРОЧНО дано а1а2а3а4 ромб а1а3 24 а2а4 10 найти sполн?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Х + х + 5 = 50 2х + 5 = 50 2х = 50 — 5 = 45 х = 45 : 2.

Решим системой a — b = 30 a + b = 180 2a = 210 a = 105 b = 75.

Α — β = 30, α = 30 + β, α + β = 180°, подставляем значение α 30 + β + β = 180°, 2β = 180 — 30 = 150°, β = 75°, α = 30 + β = 30 + 75 = 105° Ответ : α = 105°, β = 75°.

49 — 15 = 34 34 / 2 = 17 катет напротив угла 30гр(120 — 90) равен половине гипотенузы = 17 * 2 = 34 34 + 34 + 49 + 15 = 132.

Доказательство основано на признаке параллельности прямых, признаке равенства треугольников и признаке параллелограмма.

🎦 Видео

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

§ 12 № 1- 29 - Геометрия 7-9 класс ПогореловСкачать

№ 201-300 - Геометрия 9 класс МерзлякСкачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

16-я задача ЕГЭ (планиметрическая). Видеоурок №2Скачать

Повторение изученного в 8 классе Геометрия все темы просто! Вся геометрия 8 в одном уроке. ВидеоурокСкачать

№195. Найдите измерения прямоугольного параллелепипеда AD1, если АС1 = 12 см и диагональ BD1Скачать

№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать