Мгновенный центр скоростей окружности (4 видео)

iSopromat.ru

Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.

Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например P_V, C_V.

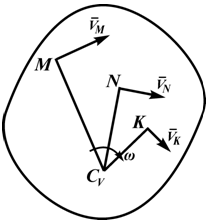
При определении положения МЦС скорость любой точки может быть записана: V_M = V_Cv + V_MCv , где точка C_V выбрана за полюс. Поскольку это МЦС и V_Cv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:

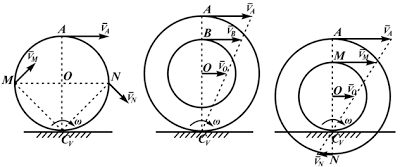
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:

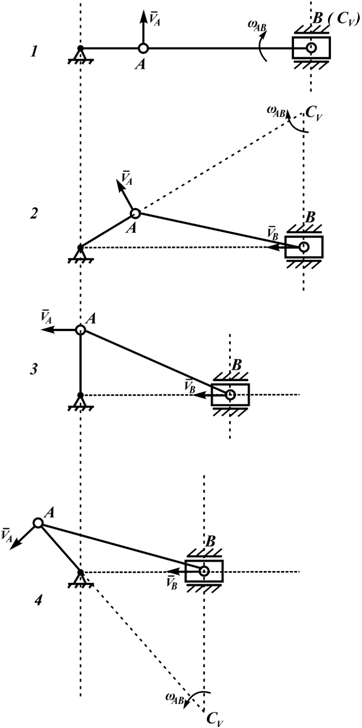
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.

На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.

В этом случае МЦС находится в «бесконечности», т.е.

V_A/2R=V₀/R=V_M/(R√2)=ω,
V_A/2R=V₀/R=V_B/(R+r)=ω,
V_A/(R+r)=V₀/r=V_N/(R-r)=ω

Формулы справедливы при отсутствии проскальзывания в точке C_V.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Содержание

Решение задач, контрольных и РГР
Набор студента для учёбы
Мгновенный центр скоростей (МЦС)
Мгновенный центр скоростей
Сложное движение точки
🔥 Видео

Видео:Мгновенный центр вращенияСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Мгновенный центр скоростейСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Мгновенный центр скоростейСкачать

Мгновенный центр скоростей (МЦС)

Зависимость (8.4) позволяет получить простую картину распределения скоростей точек плоской фигуры. Это распределение оказывается точно таким же, как и в случае тела, вращающегося вокруг неподвижной оси. Разница лишь в том, что точка, вокруг которой вращается плоская фигура, со временем изменяет свое положение, т.е. является мгновенным центром вращения.

Мгновенным центром скоростей (или мгновенным центром вращения) называют ту точку плоской фигуры, скорость которой в данный момент времени равна нулю. Покажем, что если угловая скорость фигуры отлична от нуля (со Ф 0), то такая точка существует и единственна.

Пусть в некоторый момент времени известна скорость _А точки А фигуры и угловая скорость фигуры со Ф 0.

Проведем прямую AN, перпендикулярную вектору Уд, и отложим на ней (рис. 8.8) отрезок

Найдем скорость точки Р фигуры при помощи векторной формулы (8.4):

Оба вектора в правой части этого равенства перпендикулярны к AN, т.с. параллельны друг другу, и направлены в противоположные стороны (рис. 8.8). Модули их равны, т.к. согласно (8.5)

Поэтому vр = у_л + у_Рд = 0, следовательно, точка Р является мгновенным центром скоростей (МЦС) фигуры. Единственность МЦС следует из процедуры его построения.

Пусть точка Р — мгновенный центр скоростей плоской фигуры, тогда скорость любой точки фигуры выражается в виде

Здесь _ВР — это вектор скорости точки В при вращении фигуры вокруг центра Р с угловой скоростью со, вектор _в = _ВР направлен перпендикулярно отрезку РВ в сторону вращения фигуры (рис. 8.9), а его величина согласно (8.5)

Это значит, что скорость любой точки фигуры находится так, как если бы фигура вращалась в своей плоскости с угловой скоростью со вокруг МЦС (рис. 8.9).

Из равенств v_B = со ? ВР и v_c = со- СР следует пропорция

т.е. величина скорости точки плоской фигуры пропорциональна её расстоянию от МЦС.

Для решения задач кинематики плоского движения удобно пользоваться следующими правилами построения МЦС.

1. Как видно из рис. 8.9, МЦС — это точка пересечения перпендикуляров к скоростям точек плоской фигуры. Поэтому для построения МЦС достаточно знать направления скоростей двух точек фигуры (при условии, что эти скорости непараллельны).

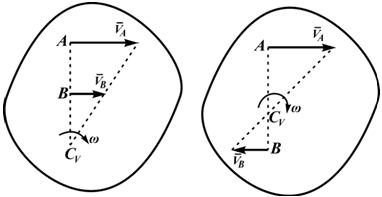
2. Если скорости двух точек фигуры параллельны, а сами эти точки лежат на общем перпендикуляре к скоростям (рис. 8.10), то положение МЦС можно установить при помощи пропорции (8.9), если известны величины и направления скоростей. Решение пропорции (8.9) можно заменить простым геометрическим построением, показанным на рис. 8.9 штриховой линией: МЦС находится как точка пересечения общего перпендикуляра ВС и линии, соединяющей концы векторов скоростей точек В и С.

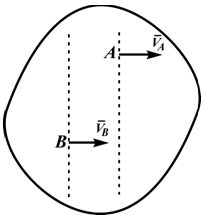
3. Если перпендикуляры к скоростям точек параллельны, т.е. не имеют пи одной общей точки (рис. 8.11), то МЦС построить невозможно. Построения (п.8.4) допускают такую ситуацию лишь в том случае, когда угловая скорость фигуры со = 0. Тогда из (8.4) и (8.5) следует, что все точки фигуры имеют одинаковые скорости.

4. Если известна скорость _А какой-нибудь точки А фигуры и угловая скорость фигуры со, то можно найти МЦС, повторяя построения п. 4.4.
5. При качении фигуры по неподвижной кривой без проскальзывания МЦС фигуры находится в точке К её касания с этой кривой (рис. 8.12), так как скорость точки касания фигуры равна нулю.

Продемонстрируем использование МЦС для расчета скоростей.

Пример 2. Стержень АВ длиной 0,6 м совершает плоскопараллельное движение так, что его концы А и В перемещаются вдоль вертикальРешение. Найдем положение МЦС стержня АВ. Для этого построим перпендикуляры к скоростям точек А и В (рис. 8.14). Точка пересечения Р этих перпендикуляров и является МЦС стержня.

ной и горизонтальной направляющих (рис. 8.13). Известно, что точка А движется с постоянной скоростью гд = 2 м/с.

Найти угловую скорость стержня АВ и скорость точки В в тот момент времени, когда угол (р= 30°.

Согласно описанным выше свойствам МЦС (и. 8.4) имеем:

Из первого равенства находим угловую скорость стержня

Из второго равенства определяем величину скорости точки В:

Направления скоростей у_д , v_в и направление вращения стержня А В согласованы так, как показано на рис. 8.14.

Видео:§4.3. Мгновенный центр скоростей (часть 1)Скачать

Мгновенный центр скоростей

Мгновенным центром скоростей (МЦС) называется точка в плоскости движения плоской фигуры, скорость которой в данный момент равна нулю.

МЦС является мгновенной неподвижной осью. Поэтому векторы скоростей точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, и направлены в соответствии с угловой скоростью, а модули скоростей пропорциональны расстояниям точек до МЦС: . Отношение скорости любой точки плоской фигуры к ее расстоянию до МЦС является величиной, равной угловой скорости вращения.

Частные случаи определения МЦС

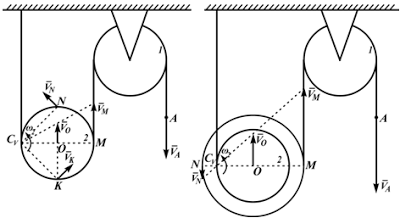
а) Колесо катится без скольжения. МЦС находится в точке соприкосновения колеса с неподвижной поверхностью:

б) четырехзвенник ОАВО₁. Строим МЦС стержня АВ. Перпендикуляры к скоростям точек А и В будут параллельны, т. е. пересекаются в бесконечности. Поэтому МЦС не существует. Стержень АВ совершает мгновенное поступательное движение, и скорости всех точек стержня будут одинаковыми по величине и направлению. В данный момент угловая скорость стержня АВ равна нулю (_AB = 0 ).

Видео:Мгновенный центр скоростей колесаСкачать

Сложное движение точки

Сложным движением называют такое движение, при котором точка одновременно участвует в двух или более движениях Абсолютным движением называют движение точки М по отношению к основной системе отсчета O₁X₁Y₁Z₁, которую условно принимают за неподвижную. Относительным движением называют движение точки М по отношению к подвижной системе отсчета OXYZ. Переносным движением называют движение подвижной системы отсчета OXYZ относительно основной (неподвижной) системы отсчета O₁X₁Y₁Z_1.

Теорема о сложении скоростей

Абсолютной скоростью называют скорость точки М относительно основной системы координат O₁X₁Y₁Z₁ и обозначают

Относительной скоростью называют скорость точки М относительно подвижной системы координат OXYZ и обозначают

Переносной скоростью называют скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка М, и обозначают

Абсолютная скорость точки в сложном движении равна геометрической сумме переносной и относительной скоростей =+

Модуль абсолютной скорости в общем случае находят проектированием выражения на оси координат, так как угол между векторами относительной и переносной скоростей может быть от 0 до 180°: