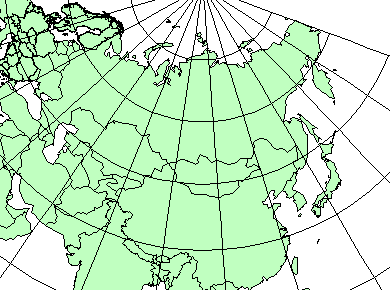
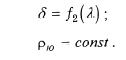В каких проекциях параллели изображаются концентрическими окружностями (6 видео)

Классификация проекций по виду нормальной картографической сетки

Азимутальные проекции – этопроекции, в которых параллели изображаются концентрическими окружностями, а меридианы – прямыми, исходящими из общего центра параллелей, под углами, равными разности их долгот (рис. 2.15).

Рис. 2.15. Азимутальная проекция

Конические проекции – этопроекции, в которых параллели изображаются дугами концентрических окружностей, а меридианы – прямыми, расходящимися из общего центра параллелей, под углами, равными разности их долгот (рис. 2.16).

Рис. 2.16. Коническая проекция

Цилиндрические проекции – этопроекции, в которых меридианы изображаются равноотстоящими параллельными прямыми, а параллели перпендикулярными к ним прямыми, в общем случае не равноотстоящими (рис.2.17).

Рис. 2.17. Цилиндрическая проекция

Псевдоазимутальные проекции – этопроекции, в которых параллели изображаются концентрическими окружностями, меридианы – кривыми, сходящимися в точке полюса, средний меридиан – прямой.

Псевдоконические проекции – этопроекции, в которых параллели изображаются дугами концентрических окружностей, средний меридиан – прямой, проходящей через их общий центр, остальные меридианы – кривые.

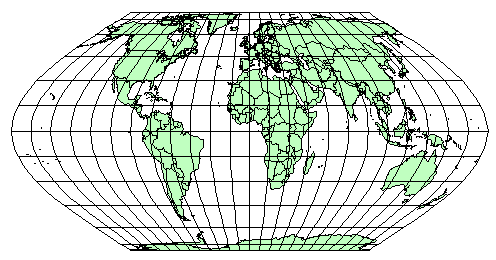
Псевдоцилиндрические проекции – этопроекции, в которых параллели изображаются параллельными прямыми, средний меридиан – прямая, перпендикулярная к параллелям, остальные меридианы – кривые или прямые, наклоненные к параллелям (рис. 2.18).

Рис. 2.18. Псевдоцилиндрическая проекция

Полиазимутальные проекции – этопроекции, в которых параллели изображаются эксцентрическими окружностями, меридианы – кривые, сходящиеся в точке полюса, средний меридиан – прямой.

Поликонические проекции – этопроекции, в которых параллели изображаются дугами эксцентрических окружностей с радиусами тем большими, чем меньше их широта, средний меридиан – прямой, на которой расположены центры всех параллелей, остальные меридианы – кривые (рис. 2.19).

Содержание

Проекции с параллелями постоянной кривизны
Виды картографических проекций
Что такое картографическая проекция?
Цилиндрическая проекция
Коническая проекция карты
Азимутальная картографическая проекция
5.3. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ
5.3.1. Равноугольные проекции
5.6.2. Равнопромежуточные проекции
5.6.3. Равновеликие проекции
5.6.4. Произвольные проекции
7.10. СПОСОБ КОЛИЧЕСТВЕННОГО ФОНА
ArcGIS автоматически интегрирует данные в известных системах координат
Методы получения проекций
7.1. КАРТОГРАФИЧЕСКАЯ СЕМИОТИКА
5.6. ВЫБОР ПРОЕКЦИЙ
7.8. СПОСОБ АРЕАЛОВ.
5.7. РАСПОЗНАВАНИЕ ПРОЕКЦИЙ
🎦 Видео

Видео:58.2.1. Построить недостающие проекции точек, принадлежащих поверхности сферы, определить их видимСкачать

Проекции с параллелями постоянной кривизны

· Параллели прямые линии. Описывается уравнениями, выраженными только в прямоугольной системе координат. Включает 4 класса проекций

a) Цилиндрические проекции (меридианы — равностоящие параллельные прямые, а параллели – параллельные прямые, ортогональные меридианам). Их общие уравнения х=f(φ) и y=βλ

Где β – параметр проекции

b) обобщенные цилиндрические проекции (меридианы – неравностоящие параллельние прямые, а параллели – параллельные прямые,ортогональные меридианам. Об. Ур-е х=f₁(φ) и х=f₂(λ)

c)Псевдоцилиндрические проекции (параллели – параллельные прямые, меридианы – кривые или прямые симметричные относительно среднего прямолинейного меридиана.

d) цилиндрическо-конические проекции, в которых параллели изображаются пучком прямых, а меридианы – концентрическими окружностями.

· Конические окружности. Выражаются в системах плоских полярных и прямоугольных координат.

a) Конически епроекции (параллели – концентрические окружности, а меридианы – пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ пропорциональны углам между ними на поверхности эллипсоида (шара). В точке полюса Р имеется разрыв изображения. Ур-я

b) Обобщенные конические проекции (параллели – конц окружности, меридианы — пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ являются функциями этих углов на эллипсоиде (шаре). В точке полюса Р имеется разрыв.

c) Псевдоконические проекции (параллели — концентрические окружности, меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

d) Азимутальные проекции (параллели -концентрические окружности, меридианы — пучок прямых, исходящих из центра окружности). В точке полюса отсутствует разрыв изображения. Углы между меридианами на проекции равны углам между ними на шаре (эллипсоиде). Плоские полярные координаты выражаются в функции полярных сфероидических (сферических) координат z=const, a=const. Уравнения

e) Обобщенные азимутальные проекции (параллели -концентрические окружности, меридианы — пучок прямых, исходящих из центра окружности, углы между ними являются функциями этих углов на эллипсоиде, в точке полюса отсутствует разрыв изображения. Меридианы с долготами 0 и 360 совпадают). Уравнения

f) Псевдоазимутальные проекции. Параллели – конц. Окр, в точке полюса нет разрыва изображения. Меридианы с долготами 0 и 360 совпадают и являются либо прямыми либо кривыми, в каждой точке которых они имеют одинаковую кривизну, остальные меридианы – прямые или кривые линии. Уравнения

· Эксцентрические окружности. Выражаются в плоских и прямоугольных координатах.

a) Поликонические проекции в широком смысле(параллели – эксцентрические окружности, центры которых находятся на среднем меридиане, а меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

b) Поликонические проекции в узком смысле. Накладывается еще два условия: полярный радиус p=Nctg φ. Частный масштаб длин на среднем меридиане имеет постоянное значение m₀=k, в частности m₀=1.

2) Картографические проекции с параллелями переменной кривизны

· Полиазимутальные проекции и обобщенные полиазимутальные проекции

a) Полиазимутальные проекции. Параллели-эллипсы, меридианы – пучок прямых или кривых, исходящих из центра эллипсов, в точке полюса отсутствует разрыв изображения. Общие уравнения

b) Обобщенные полиазимутальные (параллели – кривые произвольной кривизны, а меридианы пучок прямых или кривых, исходящих из точки полюса, в котором нет разрыва изображения). Общие уравнения

· Обобщенные поликонические, различающиеся изображением параллелей; в виде – эллипсов, парабол, гипербол и параллелями произвольной кривизны, меридианы изображаются кривыми линиями. Обобщенные уравнения

· Полицилиндрические проекции. Параллели и меридианы изображаются кривыми произвольной или заданной кривизны (эллипсами, параболами и гиперболами)

Общие уравнения

· Проекции произвольных поверхностей, картографическая сетка которых отражает форму картографических поверхностей. Обобщение азимутальных, цилиндрических, конических и др проекций.

· Проекции для создания аноморфированных карт, обладающие дополнительными функциональными возможностями:

a) Варивалентные проекции

b) Переменно-масштабные проекции (при сохранении общего масштаба карты достигается сжатие или растяжение изображения на ее отдельных участках

c) Проекции с измененной метрикой пространства (исп эвклидова метрика и др метрики)

Видео:42 Картографические проекцииСкачать

Виды картографических проекций

Видео:Метод эксцентрических сферСкачать

Что такое картографическая проекция?

Картографическая проекция — это способ сгладить трехмерную поверхность земного шара (или другого сферического тела) в плоскость для того, чтобы сделать карту. Это требует систематического преобразования широт и долгот местоположений поверхности сферы в местоположения на плоскости. Этот процесс обычно математический, но некоторые методы основаны на графике.

Все проекции имеют искажения. Они бывают следующих видов: искажения форм, искажения площадей, искажения длин, искажения углов. Особенно большими искажения бывают на мелкомасштабных картах, на крупномасштабных они практически неощутимы.

Цилиндрическая проекция

Цилиндрические картографические проекции являются одним из способов изображения Земли. В этом виде проекции параллели нормальной сетки параллельные прямые, а меридианы перпендикулярные параллелям прямые; расстояния между ними пропорциональны разностям долгот. Единственный фактор, который отличает разные цилиндрические проекции друг от друга, — это масштаб, используемый при разнесении параллельных линий на карте.

Цилиндрические проекции. Равноугольная Меркатора

Недостатки цилиндрических проекций в том, что они сильно искажены на полюсах. Хотя области вблизи экватора с большей вероятностью будут точными в сравнению с реальной Землей, параллели и меридианы, являющиеся прямыми линиями, не учитывают искривление Земли. Цилиндрические отлично подходят для сравнения широт друг с другом и полезны для обучения и визуализации мира в целом, но на самом деле не являются наиболее точным способом визуализации того, как мир действительно выглядит в целом.

Типы цилиндрических картографических проекций, которые вы можете знать, включают в себя популярные проекции Меркатора, Кассини, Гаусса-Крюгера, Миллера, Бермана, Хобо-Дайера и Галла-Петерса.

Коническая проекция карты

Канонические проекции включают эквидистантную коническую проекцию, конформную коническую проекцию Ламберта и конику Альберса. Эти карты имеют конусную константу, которая определяет угловое расстояние между меридианами. Эти меридианы являются равноотстоящими и прямыми линиями, которые сходятся в местах вдоль проекции независимо от того, есть ли полюс или нет. Как и цилиндрическая проекция, проекции конической карты имеют параллели, которые пересекают меридианы под прямым углом с постоянной мерой искажения повсюду.

Проекции конической карты разработаны так, чтобы их можно было обернуть вокруг конуса на вершине сферы (шара), но они не должны быть геометрически точными.

Проекция Альберса является примером проекции конической карты

Конические проекции лучше всего подходят для использования в качестве региональных карт или карт полушария, редко для полной карты мира. Искажение на конической карте делает его неподходящим для использования в качестве визуального изображения всей Земли, но делает его отличным для визуализации умеренных регионов, карт погоды, климатических проекций и многого другого.

Азимутальная картографическая проекция

В азимутальной проекции параллели нормальной сетки являются концентрическими кругами, а меридианы — их радиусами, расходящимися из общего центра параллелей под углами, равными разности долгот. Каждая точка на карте имеет тот же самый азимут по отношению к среднему меридиану, который эта же точка имеет со средним меридианом на сфере.

Азимутальная равновеликая проекция Ламберта

Эквидистантная азимутальная проекция с северного полюса

Азимутальная картографическая проекция является угловой — учитываются три точки на карте (A, B и C), азимут от точки B до точки C определяет угол, на который кто-то должен смотреть или двигаться, чтобы добраться до A. Эти угловые отношения более известны как дуги большого круга или геодезические дуги. Азимутальные карты полезны для определения направления в любой точке Земли, используя центральную точку в качестве ориентира.

Видео:10класс. Картографические проекцииСкачать

5.3. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ

Для различных целей создаются различные по характеру искажений проекции. Характер искажений проекции определяется отсутствием в ней определенных искажений (углов, длин, площадей). В зависимости от этого все картографические проекции по характеру искажений подразделяются на четыре группы:
— равноугольные (конформные);
— равнопромежуточные (эквидистантные);
—равновеликие (эквивалентные);
— произвольные.

5.3.1. Равноугольные проекции

Равноугольными называются такие проекции, в которых направления и углы изображаются без искажений. Углы, измеренные на картах равноугольных проекций, равны соответствующим углам на земной поверхности. Бесконечно малая окружность в этих проекциях всегда остается окружностью.
В равноугольных проекциях масштабы длин в любой точке по всем направлениям одинаковы, поэтому у них нет искажения формы бесконечно малых фигур и нет искажения углов (рис. 5.7, Б). Это общее свойство равноугольных проекций выражает формула ω = 0°. Но формы реальных (конечных) географических объектов, занимающих целые участки на карте, искажаются (рис. 5.8, а). У равноугольных проекций наблюдаются особенно большие искажения площадей (что отчетливо демонстрируют эллипсы искажений).

Рис. 5.7. Вид эллипсов искажений в проекциях равновеликих —- А, равноугольных — Б, произвольных — В, в том числе, равнопромежуточных по меридиану — Г и равнопромежуточных по параллели — Д. На схемах показано искажение угла 45°.

Эти проекции используются для определения направлений и прокладки маршрутов по заданному азимуту, поэтому их всегда используют на топографических и навигационных картах. Недостатком равноугольных проекций является то, что в них сильно искажаются площади (рис. 5.7, а).

Рис. 5.8. Искажения в цилиндрической проекции:а – равноугольной; б – равнопромежуточной; в – равновеликой

5.6.2. Равнопромежуточные проекции

Равнопромежуточными проекциями называют проекции, у которых масштаб длин одного из главных направлений сохраняется (остается неизменным) (рис. 5.7, Г. рис. 5.7, Д.) Применяются главным образом для создания мелкомасштабных справочных карт и карт звездного неба.

5.6.3. Равновеликие проекции

Равновеликими называются проекции, в которых нет искажений площадей, т. е. площадь фигуры, измеренной на карте, равна площади этой же фигуры на поверхности Земли. В равновеликих картографических проекциях масштаб площади повсюду имеет одну и ту же величину. Это свойство равновеликих проекций можно выразить формулой:

P = a× b = Const = 1 (5.15)

Неизбежным следствием равновеликости этих проекций является сильное искажение у них углов и форм, что хорошо поясняют эллипсы искажений (рис. 5.7, A).

5.6.4. Произвольные проекции

К произвольным относятся проекции, в которых имеются искажения длин, углов и площадей. Необходимость использования произвольных проекций объясняется тем, что при решении некоторых задач возникает необходимость в измерении углов, длин и площадей на одной карте. Но ни одна проекция не может быть одновременно и равноугольной, и равнопромежуточной, и равновеликой. Ранее уже говорилось, что с уменьшением изображаемого участка поверхности Земли на плоскости уменьшаются и искажения изображения. При изображении небольших участков земной поверхности в произвольной проекции величины искажений углов, длин и площадей незначительны, и при решении многих задач их можно не учитывать.

Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

7.10. СПОСОБ КОЛИЧЕСТВЕННОГО ФОНА

Этот способ, как и способ качественного фона, отображает подразделение территории на однородные районы, но по количественному показателю (или показателям). Для этого по имеющимся источникам выделяют согласно разработанной ступенчатой шкале однородные районы, которые затем раскрашивают цветом разной насыщенности или покрывают соответствующими штриховками. При применении количественного фона линии на карте разграничивают выделенные однородные районы, причем смежные районы могут передавать величину явления, соответствующую противоположным ступеням шкалы.
Для использования этого способа требуется хорошая изученность территории по определенным показателям в количественном отношении. Очень часто для построения карт необходимо выполнение картографических работ, например составление морфометрических карт по топокартам (густоты и глубины расчленения рельефа, крутизны склонов и др.).
Способ количественного фона используется главным образом для составления карт природы (геоморфологических, гидрологических, гидрогеологических и др.), но его можно встретить и на социально-экономических картах, например на картах плотности населения.

Рис. 7.10. Количественный фон.

Возможно сочетание качественного и количественного фонов, например при выделении районов преобладающих конфессий (качественный фон) с дополнительной характеристикой процентного соотношения населения разного вероисповедания (количественный фон).

Вопросы и задания для самоконтроля

Как называют научную дисциплину, исследующую свойства знаков и знаковых систем?
Какие разделы включает картографическая семиотика? Дайте им характеристику.
Что включает понятие «Язык карты»?
Назовите основные функции языка карты? Дайте этим функциям характеристику.
С какой целью используют картографические условные знаки?
На какие основные группы подразделяют условные знаки? Дайте им характеристику.
С какой целью используют графические переменные? Приведите примеры графических переменных.
Какие функции выполняют значки на географических картах? Приведите примеры использования способа значков?
Как различают значки по форме? Дайте каждой форме значка характеристику.
Какие значки используются для передачи динамики явлений?
С какой целью применяют линейные знаки?
Дайте определение изолинии.
С какой целью применяют изолинии? Приведите примеры изолиний.
Каковы количественные и качественные показатели земной поверхности можно показать с помощью изолиний?
Как называют линии, отображающие распределение дискретных объектов?
Для характеристики каких географических явлений применяют способ качественного фона?
Какие графические средства применяют для показа географических явлений способом качественного фона?
Какие явления показывают с помощью количественного фона?
Какие графические средства применяют для показа географических явлений способом количественного фона?

Далее
Главная
Предыдущая

Видео:Стереографические проекции. Часть 1. Элементы проекцииСкачать

ArcGIS автоматически интегрирует данные в известных системах координат

Все географические данные, используемые в ArcGIS, предполагают наличие корректной системы координат, что позволяет им быть локализованными на реальной земной поверхности.

Если данные имеют корректную систему координат, ArcGIS может автоматически интегрировать их «на лету» с другими спроецированными данными в соответствующую среду – для картографирования, трехмерной визуализации, анализа и т.д.

Если данные не имеют пространственной привязки, их невозможно интегрировать. Необходимо определить ее до того, как вы начнете использовать эти данные в ArcGIS. Пространственная привязка (система координат) является метаданными. Она описывает систему координат, которую используют данные.

Видео:2 3 проекция точки на конусеСкачать

Методы получения проекций

Изучая картографические проекции, их виды и свойства необходимо упомянуть о методах их построения. Итак, картографические проекции получают, используя два основных метода:

В основе геометрического метода лежат закономерности линейной перспективы. Наша планета условно принимается сферой некоторого радиуса и проецируется на цилиндрическую или коническую поверхность, которая может либо касаться, либо рассекать ее.

Проекции, полученные подобным способом, называются перспективными. В зависимости от положения точки наблюдения относительно поверхности Земли перспективные проекции разделяют на виды:

гномонические или центральные (когда точка зрения совмещена с центром земной сферы);
стереографические (в этом случае точка наблюдения расположена на поверхности относимости);
ортографическая (когда поверхность наблюдается из любой точки, находящейся вне сферы Земли; проекция строится переносом точек сферы с помощью параллельных линий, перпендикулярных к отображающей поверхности).

Аналитический метод построения картографических проекций базируется на математических выражениях, связывающих точки на сфере относимости и плоскости отображения. Такой метод является более универсальным и гибким, позволяя создавать произвольные проекции по заранее заданному характеру искажения.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

7.1. КАРТОГРАФИЧЕСКАЯ СЕМИОТИКА

Язык карты – это используемая в картографии знаковая система, включающая условные обозначения, способы изображения, правила их построения, употребления и чтения при создании и использовании карт. Во все времена язык карты не только обеспечивал хранение и передачу пространственно-временной информации, но и играл роль общего языка в науках о Земле и смежных с ними отраслях знания.
На стыке картографии и семиотики – лингвистической науки, исследующей свойства знаков и знаковых систем, сформировался особый раздел картографическая семиотика, в рамках которой разрабатывается общая теория систем картографических знаков как языка карты.
В ней изучается довольно обширный круг проблем, касающихся происхождения, классификации, свойств и функций картографических знаков и способов картографического изображения. Семиотика включает три основных раздела: синтактику, семантику и прагматику, соответственно эти разделы существуют и в картографической семиотике:
картографическая синтактика – изучает правила построения и употребления знаковых систем, их структурные свойства, грамматику языка карты;
картографическая семантика – исследует соотношения условных знаков с самими отображаемыми объектами и явлениями;
картографическая прагматика – изучает информационную ценность знаков как средства коммуникации и особенности их восприятия читателями карты. Иногда в составе картографической семиотики выделяют еще один раздел – картографическую стилистику, изучающую стили и факторы, которые определяют выбор изобразительных средств в соответствии с назначением и функциями картографических произведений.
Исследования показали, что в языке карты можно различить, по крайней мере, два слоя (подъязыка): один из них отражает размещение картографируемых объектов, их пространственную форму, ориентацию, взаимное положение, другой – содержательную сущность этих явлений, их внутреннюю структуру, качественные и количественные характеристики. Грамматика обоих подъязыков определяется правилами картографической семиотики.
Язык карты – это объектный язык картографии. Его главные функции (как и картографии вообще) – коммуникативная, т.е. передача некоторого объема информации от создателя карты к читателю, и познавательная – получение новых знаний о картографируемом объекте.

Видео:Метод концентрических сфер.Скачать

5.6. ВЫБОР ПРОЕКЦИЙ

На выбор проекций влияет много факторов, которые можно сгруппировать следующим образом:

географические особенности картографируемой территории, ее положение на Земном шаре, размеры и конфигурация;
назначение, масштаб и тематика карты, предполагаемый круг потребителей;
условия и способы использования карты, задачи, которые будут решаться по карте, требования к точности результатов измерений;
особенности самой проекции – величины искажений длин, площадей, углов и их распределение по территории, форма меридианов и параллелей, их симметричность, изображение полюсов, кривизна линий кратчайшего расстояния.

Первые три группы факторов задаются изначально, четвертая – зависит от них. Если составляется карта, предназначенная для навигации, обязательно должна быть использована равноугольная цилиндрическая проекция Меркатора. Если картографируется Антарктида, то почти наверняка будет принята нормальная (полярная) азимутальная проекция и т.д.
Значимость названных факторов может быть различной: в одном случае на первое место ставят наглядность (например, для настенной школьной карты), в другом – особенности использования карты (навигация), в третьем – положение территории на земном шаре (полярная область). Возможны любые комбинации, а следовательно – и разные варианты проекций. Тем более что выбор очень велик. Но все же можно указать некоторые предпочтительные и наиболее традиционные проекции.Карты мира обычно составляют в цилиндрических, псевдоцилиндрических и поликонических проекциях. Для уменьшения искажений часто используют секущие цилиндры, а псевдоцилиндрические проекции иногда дают с разрывами на океанах.Карты полушарий всегда строят в азимутальных проекциях. Для западного и восточного полушарий естественно брать поперечные (экваториальные), для северного и южного полушарий – нормальные (полярные), а в других случаях (например, для материкового и океанического полушарий) — косые азимутальные проекции.Карты материков Европы, Азии, Северной Америки, Южной Америки, Австралии с Океанией чаще всего строят в равновеликих косых азимутальных проекциях, для Африки берут поперечные, а для Антарктиды – нормальные азимутальные.Карты отдельных стран, административных областей, провинций, штатов выполняют в косых равноугольных и равновеликих конических или азимутальных проекциях, но многое зависит от конфигурации территории и ее положения на земном шаре. Для небольших по площади районов задача выбора проекции теряет актуальность, можно использовать разные равноугольные проекции, имея в виду, что искажения площадей на малых территориях почти неощутимы.Топографические карты Украины создают в поперечно-цилиндрической проекции Гаусса, а США и многие другие западные страны – в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно UТМ). Обе проекции близки по своим свойствам; по существу та и другая являются многополостными.Морские и аэронавигационные карты всегда даются исключительно в цилиндрической проекции Меркатора, а тематические карты морей и океанов создают в самых разнообразных, иногда довольно сложных проекциях. Например, для совместного показа Атлантического и Северного Ледовитого океанов применяют особые проекции с овальными изоколами, а для изображения всего Мирового океана – равновеликие проекции с разрывами на материках.
В любом случае при выборе проекции, в особенности для тематических карт, следует иметь в виду, что обычно искажения на карте минимальны в центре и быстро возрастают к краям

Кроме того, чем мельче масштаб карты и обширнее пространственный охват, тем большее внимание приходится уделять «математическим» факторам выбора проекции, и наоборот – для малых территорий и крупных масштабов более существенными становятся «географические» факторы

Видео:Лекция 5. Поверхности вращения. часть 1.Скачать

7.8. СПОСОБ АРЕАЛОВ.

Способ ареалов (от латинского слова area — площадь, участок) заключается в том, что площадь, на которой распространено картографируемое явление, особым обозначением выделяется из всей изображенной на карте территории. Применяется главным образом для качественной характеристики картографируемой территории,
Этим способом на тематических картах показывают области распространения культурных и диких видов растений или животных, бессточные области, районы плавучих льдов в море, районы залегания полезных ископаемых, на исторических картах могут быть показаны территории, охваченные крестьянскими восстаниями, и многие другие явления.
Ареалы бывают абсолютные, вне которых данное явление не встречается, и относительные, внутри которых данное явление обладает определенными свойствами (например, ареал промышленной разработки каменного угля в пределах области его залегания). Относительный ареал более узок – он показывает места наибольшего сосредоточения явления. Ареалы подразделяются на точные и схематичные в зависимости от использования действительных (достоверных) или мнимых границ. Если объект картографирования имеет точные границы, то и ареал будет точным. Для схематических ареалов характерно приближенное отображение явления, когда нет точных данных о его размещении или для данного явления свойственна неопределенность границ в природе.
Ареалы распространения разных видов растений, животных и т. п. могут иметь различные пространственные соотношения: они могут находиться на некотором расстоянии один от другого, могут соприкасаться друг с другом или взаимно перекрываться. Графически возможности изображения ареалов разнообразны: это сплошная или пунктирная линия различного рисунка и цвета, окраска или цветные штриховки, геометрические или наглядные значки или даже надпись (рис. 7.7).

Рис. 7.7. Графические способы показа ареала на карте

Границы как графическое средство, преимущественно применяются для абсолютных ареалов, для относительных – значки или надписи. Причем, отличие значка ареала от значка значкового способа заключаются в том, что в первом случае он характеризует площадь, а во втором – показывает объект точно, локализовано. Границы показывают не линейный объект, а только оконтуривают ареал.
На карте «Австралия, Новая Зеландия. Месторождения полезных ископаемых» (рис. 7.8), показаны важные месторождения полезных ископаемых. Металлические руды показаны химическими символами периодической системы Д.И.Менделеева, неметаллические и полиметаллические руды – геометрическими знаками разного рисунка.

Рис. 7.8. Австралия, Новая Зеландия. Месторождения полезных ископаемых

Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

5.7. РАСПОЗНАВАНИЕ ПРОЕКЦИЙ

Распознать проекцию, в которой составлена карта, – значит установить ее название, определить принадлежность к тому или иному виду, классу. Это нужно для того, чтобы иметь представление о свойствах проекции, характере, распределении и величине искажений – словом, для того, чтобы знать, как пользоваться картой, чего от нее можно ожидать.
Некоторые нормальные проекции сразу распознаются по виду меридианов и параллелей. Например, легко узнаваемы нормальные цилиндрические, псевдоцилиндрические, конические, азимутальные проекции. Но даже опытный картограф не сразу распознает многие произвольные проекции, потребуются специальные измерения по карте, чтобы выявить их равноугольность, равновеликость или равнопромежуточность по одному из направлений. Для этого существуют особые приемы: сперва устанавливают форму рамки (прямоугольник, окружность, эллипс), определяют, как изображены полюсы, затем измеряют расстояния между соседними параллелями вдоль по меридиану, площади соседних клеток сетки, углы пересечения меридианов и параллелей, характер их кривизны и т.п.
Существуют специальные таблицы-определители проекций для карт мира, полушарий, материков и океанов. Проведя необходимые измерения по сетке, можно отыскать в такой таблице название проекции. Это даст представление о ее свойствах, позволит оценить возможности количественных определений по данной карте, выбрать соответствующую карту с изоколами для внесения поправок.

ВидеоВиды проекций по характеру искажений

Вопросы для самоконтроля:

Какие элементы составляют математическую основу карты?
Что называют масштабом географической карты?
Что называют главным масштабом карты?
Что называют частным масштабом карты?
Чем обусловлено отклонение частного масштаба от главного на географической карте?
Как измерить расстояние между точками на морской карте?
Что представляет собой эллипс искажений и для каких целей он используется?
Как можно определить по эллипсу искажений наибольший и наименьший масштабы?
Какие существует методы переноса поверхности земного эллипсоида на плоскость, в чем их сущность?
Что называют картографической проекцией?
Как классифицируют проекции по характеру искажений?
Какие проекции называют равноугольными, как изобразить эллипс искажений на этих проекциях?
Какие проекции называют равнопромежуточными, как изобразить эллипс искажений на этих проекциях?
Какие проекции называют равновеликими, как изобразить эллипс искажений на этих проекциях?
Какие проекции называют произвольными?