В единичном кубе abcda1b1c1d1 найдите длину вектора ав аа1 (3 видео)

Дан единичный куб ABCDA1B1C1D1 Чему равна длина вектора: а) АВ + CD + A1C1, б)CA + DB+ А1C1; в) А1C1 + CD1 + D1А?

Содержание

Ваш ответ
Похожие вопросы
Формирование знаний и умений у обучающихся по теме «Расстояние в пространстве» в заданиях ЕГЭ
Формирование знаний и умений у обучающихся по теме «Расстояние в пространстве» в заданиях ЕГЭ
Литература
Подготовка к ЕГЭ
Просмотр содержимого документа «Подготовка к ЕГЭ»
🎥 Видео

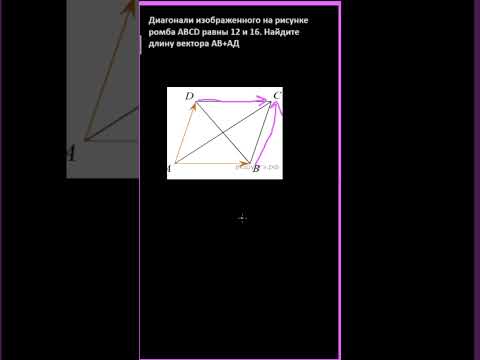
Видео:Диагонали изображенного на рисунке ромба ABCD равны 12 и 16. Найдите длину вектора АВ + АДСкачать

Ваш ответ

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Формирование знаний и умений у обучающихся по теме «Расстояние в пространстве» в заданиях ЕГЭ

Видео:Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

Формирование знаний и умений у обучающихся по теме «Расстояние в пространстве» в заданиях ЕГЭ

Для того чтобы научить решать задачи, нужно решать задачи. Однако простое следование этой рекомендации может не привести к желаемому результату, поскольку задач много, все их не перерешаешь и, кроме того, при решении последующих задач предыдущие задачи забываются. По прошествии некоторого времени ученики могут не только не помнить, как решать задачу, которую они решали раньше, но и не помнить сам факт решения этой задачи. Это объясняется тем, что в процессе решения не был отработан метод, лежащий в основе решения задач данного типа, не были сформированы устойчивые навыки и представления, необходимые для решения данной и аналогичных ей задач.

В методике обучения математике имеются примеры преодоления этих трудностей обучения решению задач. Они основаны на выделении базовых (тренировочных) задач, закладывающих основы последующего обучения решению более трудных задач. Так, например, для того чтобы научить школьников решать арифметические задачи, необходимо, чтобы сначала они овладели техникой вычислений, могли производить арифметические действия над числами, не делая при этом грубых ошибок. Аналогично, поскольку решение многих уравнений сводится к решению линейных или квадратных уравнений, то, для того чтобы научить учеников решать произвольные уравнения, нужно сначала научить их решать линейные и квадратные уравнения.

Если математика — это «гимнастика ума», то уместно провести аналогию между обучением математике и обучением гимнастике. Для того чтобы научить детей выполнять то или иное трудное гимнастическое упражнение, нужно сначала многократно повторять более легкие базовые (тренировочные) упражнения, добиваться устойчивых умений и навыков в их выполнении и только после этого переходить к обучению выполнения требуемого трудного упражнения. Более того, именно тренировки развивают такие гимнастические качества, как силу, ловкость, координацию

Так же следует поступать и в случае обучения решению геометрических задач. Сначала нужно выделить базовые (тренировочные) задачи, тренироваться в их решении до тех пор, пока не будут сформированы устойчивые умения и навыки, а затем приступать к решению более трудных задач. При этом именно тренировочные упражнения будут способствовать развитию геометрических представлений и мышления учащихся.

При обучении школьников решению стереометрических задач имеется дополнительная трудность, связанная с тем, что обычно для изображения многогранников используется параллельное проектирование, которое не вполне соответствует нашему зрительному восприятию окружающих предметов. Школьников нужно специально учить разбираться в изображениях пространственных фигур, развивать их пространственное воображение. Для этого учащихся следует познакомить с параллельным проектированием и его основными свойствами, показать, как изображаются основные пространственные фигуры.

Обучение решению задач на нахождение расстояний в пространстве не только формирует необходимые умения и навыки, но и развивает пространственные представления учащихся.

Отметим, что особенностью предлагаемых задач является то, что они хорошо клонируются. Мы рассматриваем точки и прямые на примере куба, но вместо куба можно взять прямоугольный параллелепипед, правильную треугольную или шестиугольную призму, пирамиду и т. д. Каждый учитель, по аналогии с предложенными задачами, может придумывать свои задачи. [4]

Начнем с задач на нахождение расстояния от точки до точки в пространстве.

1. Расстояние между двумя точками

Расстояние между точками А и В можно вычислить:

1) как длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон;

, где

3) по формуле .

Пример 1. В единичном кубе ABCDA1 B1 C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и F так, что D1 E = AD1 , D1 F = D1 B1 . Найдите длину отрезка EF.

Решение. Длину отрезка EF найдем по теореме косинусов из треугольника D1 EF (рис. 1), в котором D1F=, D1E=, FD1E = (треугольник AB1 D1 является равносторонним). Имеем:

откуда EF = .

Рис.1 Ответ: .

Приведем примеры данного типа задачи по 2 уровням сложности.

2. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, найдите расстояние между точками В и D.

3. В правильной шестиугольной призме A. Fl9 все ребра которой равны /3, найдите расстояние между точками А и С. (Рис. 2)

2. Расстояние от точки до прямой

Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую. (рис. 3)

Для нахождения расстояния от точки А до прямой а сначала находят основание А’ перпендикуляра, опущенного из точки А на прямую а. Если нахождение длины перпендикуляра АА’ не вытекает непосредственно из условия задачи, то на прямой а выбирают какие-нибудь точки В, С я рассматривают треугольник АВС, в котором АА’ является высотой (рис. 4). Для нахождения высоты АА’ используют теорему Пифагора или другие теоремы и формулы.

Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.

Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.

Расстояние от точки до прямой можно вычислить:

1) как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;

2) используя векторный метод;

3) используя координатно-векторный метод.

Пример 2. При условиях примера 1 найдите расстояние от точки D1 до прямой EF.

Решение. Пусть h – длина высоты треугольника D1 EF , опущенной из точки D1 . Найдем h, используя метод площадей. Площадь треугольника D1EF равна D1 F D1 E sin=.

С другой стороны площадь треугольника D1EF равна . Из уравнения находим искомое расстояние .

Замечание. Можно заметить, что выполняется равенство FE2 + D1 E2 = D1 F2, то есть треугольник D1 EF прямоугольный и длина отрезка D1 E является искомым расстоянием.

Ответ: .

2. В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой BC1 (рис. 5).

Рис. 5

Здесь для доказательства перпендикулярности прямых АВ и ВС1 можно воспользоваться тем, что прямая АВ перпендикулярна плоскости ВСС1 и, значит, перпендикулярна любой прямой, лежащей в этой плоскости. Искомое расстояние равно длине отрезка АВ и равно 1.

2′. В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой а) DС1; б) А1С1.

Так же как и в предыдущих задачах, вместо точки А можно брать любую другую вершину куба.

2». В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой СВ1 (рис. 6).

В этой задаче требуется построить (изобразить) искомый перпендикуляр. Заметим, что треугольник АСВ1 — равносторонний, следовательно, его медиана АМ будет высотой (рис. 7). Таким образом, для построения искомого перпендикуляра достаточно отметить середину М отрезка СВ1 и соединить ее с точкой А. Так как стороны треугольника АСВ1 равны , искомое расстояние равно .

2»’. В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой а) СD1; б) B1D1.

Следующие задачи наиболее трудные.

3. В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой ВD1 (рис. 8).

Для нахождения искомого перпендикуляра рассмотрим треугольник АВD1 (рис. 9). Он является прямоугольным (угол А — прямой) с катетами АВ =1, АD1 = и гипотенузой ВD1=. Найдем его высоту АN. Для этого можно использовать или преобразование подобия, или тригонометрические функции, или площадь треугольника. Искомое расстояние равно .

3′. В единичном кубе АВСDА1В1С1D1 найдите расстояние от точки А до прямой: а) DB1 ; б) СА1.

3. Расстояние от точки до плоскости

• Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.

• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.

• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.

• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.

• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

Расстояние от точки М до плоскости α

1) равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой l, которая проходит через точку М и параллельна плоскости α ;

2) равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α;

3) вычисляется по формуле, где ρ=ρ(M;α), ρ1 =ρ(M1;α), OM = r, OM1 = r1, MM1 ∩α = 0; в частности, ρ=ρ1 , если r = r1:

прямая m, проходящая через точку М, пересекает плоскость α в точке О, а точка М1 лежит на прямой m;

4) вычисляется по формуле ρ(M;α) = ρ(M; ABC) = , где треугольник

АВС расположен на плоскости α, а объем пирамиды АВСМ равен V ABCM;

5) вычисляется по формуле , где M (x0; y0; z0), плоскость α задана уравнением Ax + By + Cz + D = 0;

6) находится с помощью векторного метода;

7) находится с помощью координатно-векторного метода.

Пример 3. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние от точки С1 до плоскости АВ1 С.

Решение. Так как прямая А1 С1 параллельна АС, то прямая А1С1 параллельна плоскости АВ1 С (рис. 10). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой А1 С1 до плоскости АВ1С . Например, расстояние от центра О1 квадрата A1 B1C1 D1 до плоскости АВ1 С равно h.

Пусть Е – основание перпендикуляра, опущенного из точки О1 на прямую В1О, где О – центр квадрата ABCD. Прямая О1 Е лежит в плоскости BB1 D1 D , а прямая АС перпендикулярна этой плоскости. Поэтому О1 Е АС и

О1 Е — перпендикуляр к плоскости АВ1 С, а О1 Е = h .

Так как B1O1=,O1O=1, то .

Выражая двумя способами площадь треугольника B1O1O, получим

, откуда .

2. В кубе A. D1, ребра которого равны /2, найдите расстояние от точки В до плоскости АВ1С1 (рис. 11)

3. В единичном кубе A. D1 найдите расстояние от точки В до плоскости АСВ1.

Перейдем теперь к задачам на нахождение расстояния между двумя скрещивающимися прямыми.

4. Расстояние между скрещивающимися прямыми

Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.

Напомним, что расстоянием между двумя скрещивающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым.

Если одна из двух данных скрещивающихся прямых лежит в плоскости, а другая — параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между второй прямой и плоскостью (рис. 12).

Рис. 12

Если данные скрещивающиеся прямые а и b лежат соответственно в параллельных плоскостях и, то расстояние между прямыми а и b равно расстоянию между плоскостями и. В этом случае длина перпендикуляра СD опущенного из произвольной точки С плоскости на плоскость , будет равна расстоянию между прямыми а и b (рис. 13).

Расстояние между скрещивающимися прямыми

1) равно расстоянию от любой точки одной из тих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой;

2) равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые;

если ортогональная проекция на плоскость α переводит прямую а в точку А, а прямую b в прямую b1 , то расстояние между скрещивающимися прямыми а и b равно расстоянию от точки А до прямой b1;

4) вычисляется по формуле , где А и В – точки

на одной прямой, С и D – точки на другой прямой, ϕ — угол между данными прямыми;

5) определяется с помощью векторного метода;

6) определяется с помощью координатно-векторного метода.

Пример 4. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите расстояние между прямыми BD и SA.

Решение. Пусть Е – основание перпендикуляра (рис. 14), опущенного из точки О на ребро SA. Так как прямая BD перпендикулярна плоскости

AOS, то BD OE .

Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA.

Найдем его длину, вычислив двумя способами площадь треугольника AOS.

Из равенства AO SO = AS OE, где AO = , AS =1, SO = следует, что

OE = .

2. В единичном кубе АВСDА1В1С1D1 найдите расстояние между прямыми АА1 и ВD1 (рис. 15).

Здесь общим перпендикуляром является отрезок ЕF, соединяющий середины отрезков АА1 и ВD1 (рис. 16).

Действительно, пусть О — центр грани АВСD (рис. 17). В четырехугольнике АОЕF стороны АЕ и ОF равны и параллельны. Значит, этот четырехугольник — параллелограмм, следовательно, стороны ЕF и АО равны и параллельны.

Прямая АА1 перпендикулярна АО, так как она перпендикулярна плоскости АВС. Прямая ВD1 перпендикулярна АО по теореме о трех перпендикулярах. Следовательно. и прямая ЕF перпендикулярна АA1 и ВD1. Значит, отрезок ЕF является искомым общим перпендикуляром, длина которого равна .

2′. В единичном кубе АВСDА1В1С1D1 найдите расстояние между прямыми: а) АА1 и DВ1 ;б) АВ и СА1; в) ВС и АС1 ; г) СD и ВD1; д) АD и ВD1.

Наиболее трудной из этой серии является следующая задача.

3. В единичном кубе АВСDА1В1С1D1 найдите расстояние между прямыми АВ1 и ВС1 (рис. 18).

Расстояние между данными прямыми равно расстоянию между параллельными плоскостями АВ1D1 и ВDС1 (рис. 19).

Диагональ СА1 перпендикулярна этим плоскостям и делится ими в точках пересечения Е и F на три равные части. Следовательно, искомое расстояние равно длине отрезка ЕР и равно .

3′. В единичном кубе АВСDА1В1С1D1 найдите расстояние между прямыми: а) ВА1 и СВ1; б) ВА1 и АС; в) ВA1 и В1D1; г) ВА1 и АD1.

Можно доказать следующие утверждения.

Утверждение 1. Общий перпендикуляр двух скрещивающихся прямых существует и единственный.

Утверждение 2. Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых лежат эти прямые.

Приведенных сведений достаточно, чтобы найти расстояние между скрещивающимися прямыми в простых случаях. Расстояние между фигурами F1 и F2 обозначается р (F1, F2).

Утверждение 3. Расстояние между скрещивающимися прямыми равно расстоянию между их проекциями на плоскость, перпендикулярную одной из них.

Пусть а и b — скрещивающиеся прямые и плоскость перпендикулярна прямой а. Прямая b пересекает плоскость а в точке С (рис. 20). Пусть отрезок АВ — общий перпендикуляр прямых а и b (он существует по утверждению 1). Проекцией отрезка АВ па плоскость является отрезок А1B1, перпендикулярный отрезкам АА1 и ВВ1. Так как отрезок АВ перпендикулярен наклонной СВ, то он перпендикулярен и ее проекции СВ1 (по теореме о трёх перпендикулярах). То есть длина отрезка А1B1 есть расстояние от точки А1 (проекции прямой а на плоскость ) до прямой СВ1 (проекции прямой b на плоскость ).

Противоположные стороны АВ и А1B1 прямоугольника АВВ1А1 равны, поэтому расстояние АВ между скрещивающимися прямыми равно расстоянию А1B1 между их проекциями па плоскость , перпендикулярную прямой а, что и требовалось доказать.

Итак, если требуется найти расстояние между скрещивающимися прямыми, то постройте их общий перпендикуляр и найдите его длину; или найдите параллельные плоскости, в которых лежат данные прямые, и найдите расстояние между этими плоскостями; или спроектируйте эти прямые на плоскость, перпендикулярную одной из них, и найдите расстояние между их проекциями.

Методы решения задач

1. Поэтапно-вычислительный метод

2. Координатный метод

3. Координатно-векторный метод

4. Векторный метод

5. Метод объемов

6. Метод ключевых задач

Рассмотрим каждый метод.

1. Координатный метод

Пример 5. В единичном кубе ABCDA1 B 1C1 D1 точки Е и К — середины ребер AA1 и CD соответственно, а точка М расположена на диагонали B1 D1 так, что B1 M = 2MD1. Найдите расстояние между точками Q и L, где Q – середина

отрезка ЕМ, а L – точка отрезка МК такая, что ML = 2LK.

Решение. Введем прямоугольную систему координат, как указано на рисунке 21. Тогда E (0;0;), К (1; ;0), В1 (0;1;1) , D1 (1;0;1) . Для нахождения координат точки М используем формулу координат точки, делящей отрезок

B1 D1 в отношении 2:1. Имеем М (;; ) = (;;1) . Аналогично получим координаты точки L, делящей отрезок МК в отношении 2:1. Имеем

L (;; ) = (;; )

Координаты точки Q равны полусуммам соответствующих координат точек Е и М, поэтому Q(;; ) . Применим формулу для расстояния между точками с заданными координатами

Ответ:

Пример 6. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние от точки А1 до плоскости BDC1 .

Решение. Составим уравнение плоскости, проходящей через точки B(0;1;0), D(1;0;0) и C1 (1;1;1) рис. 22. Для этого подставим координаты этих точек в общее уравнение плоскости Ax + By + Cz + D = 0 . Получим систему уравнений

или

Отсюда находим уравнение − Dx − Dy + Dz + D =0 или x + y − z −1 = 0 . По формуле находим расстояние от точки А1 (0;0;1) до плоскости β = BDC1:

Ответ:

2. Координатно-векторный метод

Пример 7. В единичном кубе ABCDA1B1C1D1 найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .

Решение. Введем прямоугольную систему координат (рис. 23), тогда

Пусть EF – общий перпендикуляр скрещивающихся прямых BD1 и AB1 , то есть EF AB1 , EF BD1 , причем E AB1 и F BD1 . Обозначим и воспользуемся формулами для координат точки, которая делит данный отрезок в заданном отношении. Получим E (0;; ),F(;;). Пусть = p, =q, тогда E(0; p; p),F (q;1− q;q) Так как вектор Рис. 23

= (q; 1− q − p; q − p) должен быть перпендикулярным векторам = (0;1;1) и (1;- 1; 1), то имеем систему уравнений:

или

Ответ:

3. Векторный метод

Пример 8. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние от точки D1 до прямой РQ, где Р и Q – середины соответственно ребер A1 B1 и ВС.

Решение. Пусть , , (рис. 24), тогда , .

Выразим вектор через базисные векторы :

Пусть D1 N PQ , где N PQ . Выразим вектор , учитывая коллинеарность векторов и :

. Так как , то . Отсюда получаем .

. Рис. 24

Ответ:

Пример 9. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние от точки А1 до плоскости BDC1 .

Решение. Пусть , , (рис. 25), тогда , .

Выразим некоторые векторы через базисные векторы : , ,.

Пусть МА1 BDC1 , где M BDC1 . Вектор , поэтому.

Далее имеем

Так как .

, то имеем Рис. 25

Ответ:

Пример 10. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние между прямыми AB1 и BD.

Решение. Пусть , , (рис. 26), тогда , .

Если M и N – основания общего перпендикуляра прямых AB1 и BD соответственно, то имеем , ,

Вектор перпендикулярен векторам и , поэтому имеем

Рис. 26

Ответ:

4. Метод объемов

При составлении уравнения используется объем фигуры, выраженный двумя независимыми способами.

Пример 11. Ребро куба ABCDA1 B1 C1 D1 равно а. Найдите расстояние от точки С до плоскости BDC1 .

Решение. Искомое расстояние х равно высоте CQ (рис. 27), опущенной в пирамиде BCDC1 из вершины С на основание BDC1 .

Объем этой пирамиды равен

. С другой стороны, так как треугольник BDC1 равносторонний со стороной а, объем пирамиды равен

. Отсюда получаем уравнение , из которого находим

x =.

Ответ:

Метод ключевых задач

5. Метод ключевых задач

, ,

2. Найти угол между диагоналями смежных граней куба.

3. Найти угол между диагональю куба и скрещивающейся с ней диагональю грани.

4. Найти угол между диагональю куба и плоскостью, проведенной через концы трех ребер куба, выходящих из той же вершины, что и диагональ.

5. В кубе ABCDA1 B1 C1 D1 диагональ BD1 перпендикулярна плоскостям AB1 C и A1 DC1 и делится ими на три равные части.

6. Отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам.

7. В правильной треугольной пирамиде скрещивающиеся ребра перпендикулярны.

8. Отрезок, соединяющий середины скрещивающихся ребер правильного тетраэдра, является их общим перпендикуляром и имеет длину , где а – длина ребра.

9. Любое сечение треугольной пирамиды плоскостью, параллельной ее скрещивающимся ребрам, является параллелограммом.

10. Любое сечение правильной треугольной пирамиды плоскостью, параллельной ее скрещивающимся ребрам, есть прямоугольник.

Приведем пример использования метода ключевых задач.

Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, r – расстояние между ними, АВ = а , CD = b , ϕ — угол между AB и CD, V – объем пирамиды ABCD, то .

Пример 12. В единичном кубе ABCDA1 B1 C1 D1 найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .

Решение. Найдем искомое расстояние по формуле

, где V – объем пирамиды ABB1D1 (рис. 28), AB1 = , BD= ,

— угол между прямыми BD1 и AB1 . Так как площадь основания АВВ1 пирамиды ABB1 D1 равна , а высота A1 D1 равна 1, то V = . Следовательно,

Ученикам нужно показывать, что возможно одну и ту же задачу решить несколькими способами, различными методами. Предлагается рассмотреть решение одной задачи четырьмя способами: геометрическим, координатным, векторным и векторно-координатным.

Задача. В прямоугольном параллелепипеде ABCDA1B1C1D1 . Найти расстояние между (AD1) и (DB1) и вычислить его при а = 4, b = 6, с =.

1. Геометрическое решение.

Прямые AD1 и DB1 — скрещивающиеся. Чтобы найти расстояние между ними, достаточно через одну из них (например, DB1) провести плоскость П, параллельную другой прямой (AD1). Плоскость П вполне определяется прямыми (DB1) и (DE), где (DE) || (AD1). Плоскость П пересекает грани параллелепипеда по FB1PD (Рис. 29). Искомое расстояние сводится к расстоянию от произвольной точки прямой AD1 до плоскости П(EDB1). Найдем расстояние от точки D1 до плоскости EDB1.

Проведем D1K B1E. Тогда по теореме о трех перпендикулярах DK EF. Значит, плоскость DD1K пл. П. Проведем D1L DK. — искомое расстояние.

Проектируя ортогонально прямую AD1 на плоскость П, получим прямую A‘D‘1 параллельную прямой AD1. Точку пересечения прямых (A‘D‘1) и (DB‘1) обозначим через M‘. Эта точка является проекцией точки М, принадлежащей прямой (AD1).

ММ’ — искомый перпендикуляр. Длина этого перпендикуляра является расстоянием между скрещивающимися прямыми. Для вычисления этого расстояния можно найти расстояние от любой точки прямой (AD1) до плоскости П. В нашем случае (рис. 32) это D1L. Из треугольника D1EF следует ,

Из треугольника D1KD имеем и

2. Векторное решение.

Введем векторный базис. Пусть базисными векторами будут, , , а их модулями соответственно а, b и с. Найдем разложение данных векторов и по базисным (рис. 30):

Пусть MN — искомый отрезок общего перпендикуляра. Выразим вектор через базисные:

Так как и , то скалярные произведения, . Рис. 30

Из этого условия находим и.

Учитывая ортогональность базисных векторов, получим:

Из этой системы находим значения и, а затем и модуль вектора .

3. Координатное решение.

Нахождение расстояния между скрещивающимися прямыми может быть сведено, как и в первом случае к нахождению расстояния от любой точки одной прямой до плоскости, которая проходит через другую прямую, параллельно первой. Эту плоскость можно задать так: пусть Р — середина [АВ] и F — середина [D1C1 ], тогда, (PF) (AD1), а плоскость DPB1F проходит через (DB1), и (AD1) плоскости DPB1.

Выбрав в пространстве прямоугольную систему координат, найдем уравнение плоскости DPB1 а затем и расстояние от какой-нибудь точки прямой (AD1) до этой плоскости.

Пусть D(0, 0, 0) — начало координат, (DA) — ось абсцисс, (DC) – ось ординат a (DD1) — ось z — аппликат.

Тогда уравнение плоскости, определяемой точками D(0, 0, 0),

D1(0, 0, с) или А (а, 0, 0) — точки прямой (AD1). Расстояние .

4. Координатно-векторное решение.

Сущность его в том, что базисные векторы задаются координатами (a,0,0), (0,b,0), (0,0,с). Аналогично рассуждению во втором случае, находим вектор ( x,y,z) и записываем условие перпендикулярности векторов (равенство нулю скалярного произведения) тоже в координатной форме:

Предлагаемая методика тренировочных задач реализована в пособиях [1], [2], [3], в которых подробно рассмотрены не только задачи на нахождение расстояний в пространстве, но и задачи на нахождение углов, объемов, площадей поверхностей и др.

Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Литература

1. Геометрия. Стереометрия: Пособие для подготовки к ЕГЭ/ Под ред. , . – М.: МЦНМО, 2009.— 272 с.

2. Гордин должен знать каждый матшкольник. — 2-е изд., испр.— М.: МЦНМО, 2003. — 56 с.

3. Готман задачи и методы их решения.- М.: МЦНМО, 2006. – 160с.: ил.

4. , Смирнов трия. Расстояния и углы в пространстве. —М.: Экзамен, 20ЕГЭ 100 баллов).

Видео:Диагонали изображенного на рисунке ромба ABCD равны 12 и 16. Найдите длину вектора АВ - АДСкачать

Подготовка к ЕГЭ

Разновидности стереометрических задач .

Просмотр содержимого документа
«Подготовка к ЕГЭ»

ПОДГОТОВКА К ЕГЭ. СТЕРЕОМЕТРИЧЕСКАЯ ЗАДАЧА(№14).

Работа учителя математики

Разновидности стереометрических задач.

Расстояние от точки до прямой и до плоскости .
Расстояние между прямыми и плоскостями .
Угол между скрещивающимися прямыми .
Угол между прямой и плоскостью .
Угол между плоскостями .
Задача на доказательство и вычисление .
Сечения многогранников .
Объёмы многогранников .
Круглые тела: цилиндр, конус, шар.

Расстояние от точки до прямой.

Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой .

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ,

где P и Q – середины соответственно

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки С до прямой ВД1.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД 1 .

1. ∆ВСД 1 – прямоугольный ( по теореме о трёх

перпендикулярах), ∠Д 1 СВ – прямой .

2. СН – высота ∆ВСД 1 , значит СВ – среднее

пропорциональное между ВН и ВД 1 , тогда

СН – расстояние от точки С до прямой ВД 1 , поэтому СН – высота треугольника ВСД 1 . СН = 2·S ∆ВСД 1 : ВД 1 .

∆ Д 1 СВ – прямоугольный, т.к. Д 1 С  СВ

по теореме о трёх перпендикулярах .

Расстояние от точки до плоскости .

Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этого точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

В единичном кубе ABCDA₁B₁C₁D₁ найдите расстояние от точки C₁ до плоскости AB₁C.

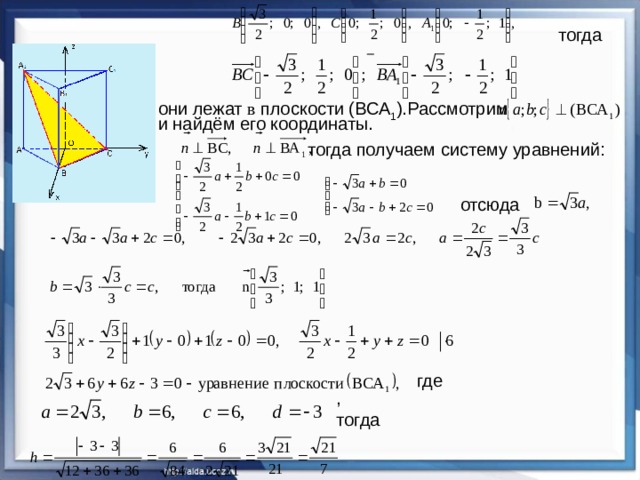
В правильной треугольной призме АВСА1В1С1–все рёбра равны 1.Найдите расстояние от точки А до плоскости (ВСА1)

Дано: АВСА 1 В 1 С 1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА 1 )

Решение: h – расстояние от точки А до плоскости (ВСА 1 ),

поэтому h – высота пирамиды АВСА 1

с основанием ВСА 1 . h =

. Пусть основанием пирамиды будет ∆АВС,

тогда её высота – АА 1 .

∆ ВСА 1 – равнобедренный, А1К – его высота, тогда

За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:

они лежат в плоскости (ВСА 1 ).Рассмотрим

и найдём его координаты.

тогда получаем систему уравнений:

Расстояние между прямыми и плоскостями .

Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр к двум скрещивающимся прямым существует и единственен.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найти: расстояние между прямыми АВ 1 и ВС 1 .

следовательно расстояние между скрещивающимися

прямыми ВС 1 и АВ 1 равно расстоянию между

соответствующими плоскостями. Диагональ СА 1

перпендикулярна этим плоскостям.

СА 1 ∩ (ВДС 1 ) = F;

CА 1 ∩ (АД 1 В 1 ) = Е.

EF – расстояние между ВС 1 и АВ 1 .

В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину отрезка АС, следовательно ОF – средняя линия треугольника АСЕ и, значит, ЕF = FC. Аналогично, О 1 Е – средняя линия треугольника А 1 С 1 F

Расстояние между скрещивающимися прямыми можно найти по формуле:

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ 1 и ВС 1 .

SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1.Найдите расстояние между прямыми АS и ВС.

Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

Угол между прямой и плоскостью .

Прямая и плоскость пересекаются , если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости .
Прямая перпендикулярна к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Проекцией точкиМна плоскость называется либо сама точка М , если М лежит в плоскости , либо точка пересечения плоскости и прямой, перпендикулярной к плоскости и проходящей через точку М , если точка М не лежит в плоскости .
Проекцией прямойaна плоскость называют множество проекций всех точек прямой a на плоскость .
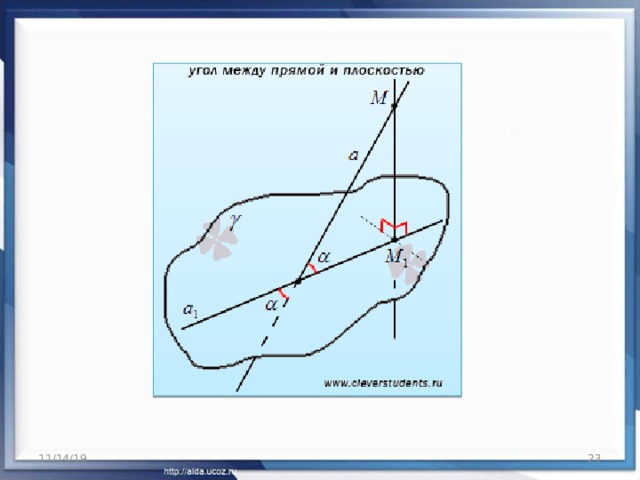
Угол между прямой и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, — это угол между прямой и ее проекцией на эту плоскость.
Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми : самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

На векторах построена пирамида. Найдите угол между прямой AD и плоскостью ABC .

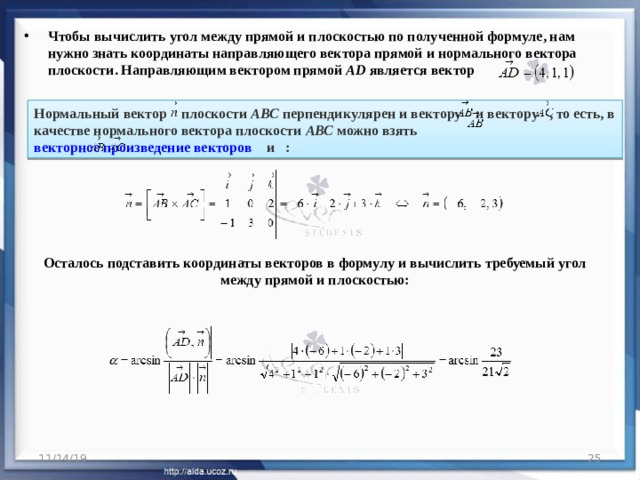
На векторах построена пирамида. Найдите угол между прямойADи плоскостьюABC .

Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямойADявляется вектор

Нормальный вектор плоскости АВС перпендикулярен и вектору и вектору , то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :

Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:

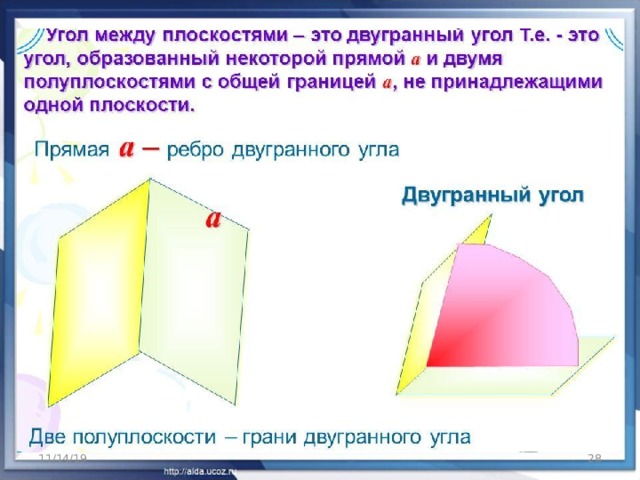
Угол между плоскостями .

Задача на доказательство и вычисление .

В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

В основании правильной треугольной призмы ABCA 1 B 1 C 1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A 1 C 1 .

а) Постройте сечение призмы плоскостью BAN .

б) Найдите периметр этого сечения.

См.сайт «Решу ЕГЭ»

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

В задачах используются в основном простейшие многогранники.

Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

что значит построить сечение многогранника плоскостью;
как могут располагаться относительно друг друга многогранник и плоскость;
как задается плоскость;
когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов. Метод вспомогательных сечений. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В правильной четырёхугольной пирамидеMABCDс вершинойMстороны основания равны 1, а боковые рёбра равны 2. ТочкаNпринадлежит ребруMC,причёмMN: NC = 2:1.Найдите площадь сечения пирамиды плоскостью, проходящей через точкиBиNпараллельно прямойAC.
См . сайт «Решу ЕГЭ»