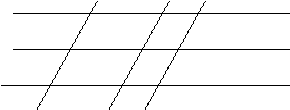
1°. Количество параллелограммов, изображенных на рисунке 1, равно
 |
2°. Длина одной из сторон параллелограмма составляет 80% от длины другой стороны. Найдите длину меньшей стороны этого параллелограмма, если его полупериметр равен 18см.
| 8см | 10см | 9см | 5см | Определить невозможно |
3°. Сумма градусных мер трех углов параллелограмма равна 300°. Найдите величину тупого угла этого параллелограмма.
| 100° | 120° | 140° | 150° | Верного ответа нет |
4°. Если сумма любых двух неравных углов четырехугольника равна 180°, то этот четырехугольник
| Может быть параллелограммом, а может и не быть | Не существует | Не может быть параллелограммом | Должен быть параллелограммом | Имеет хотя бы один прямой угол |
5°. Периметр параллелограмма равен 20 см. Какое наибольшее целое значение может принимать длина одной из диагоналей этого параллелограмма?
| Определить невозможно |
6*. О – точка пересечения диагоналей параллелограмма ABCD. Периметр треугольника ОВС на 6 больше периметра треугольника АОВ. Найдите разность длин сторон АD и DC .
| -8 | -6 | Определить невозможно |
7*. На рисунке 2 отрезки АМ и АК — высоты параллелограмма АВСD. Найдите величину угла МАК, если величина угла ADC равна 23 °.
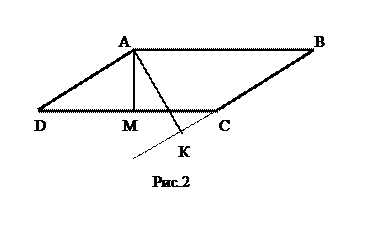 |
| 23 ° | 67 ° | 157 ° | 90 ° | Определить невозможно |
8°. Биссектриса АК угла ВАD параллелограмма АВСD делит сторону ВС на отрезки ВК=7 и КС=5. Найдите периметр этого параллелограмма.
| Верного ответа нет |
9°. Если диагональ выпуклого четырехугольника делит его на два неравных треугольника, то этот четырехугольник
| не может быть параллелограммом | может быть параллелограммом, а может и не быть | должен быть параллелограммом | не существует | имеет хотя бы один прямой угол |
10°. Если АС — диагональ четырехугольника АВСD, а медианы треугольников АВС и АDС, проведенные к стороне АС, равны между собой и лежат на одной прямой, то четырехугольник АВСD
| может быть параллелограммом, а может и не быть | должен быть параллелограммом | не может быть параллелограммом | не существует | имеет хотя бы один прямой угол |
11°. В четырехугольнике МКРТ середина отрезка МР является серединой отрезка КТ. Какому из указанных числовых промежутков принадлежит сумма длин сторон МК и КР, если периметр четырехугольника равен 20?
| (0; 9) | (9;11) | (10,5; 13) | (11;19) | Верного ответа нет |
12°. Точки М и Р лежат на противоположных сторонах параллелограмма так, что точка О пересечения диагоналей параллелограмма лежит на отрезке МР. В таком случае длина отрезка МР составляет от длины отрезка ОР
| 200% | 150% | 100% | 50% | Невозможно определить. |
13*. Диагональ КР параллелограмма КМРТ перпендикулярна стороне МК и равна
стороне ТР. Тупой угол этого параллелограмма равен
| 120° | 125° | 135° | 140° | 145° |

| 15см | 5см | 20см | Определить невозможно | 10см |
15*. Градусная мера угла между биссектрисами двух соседних углов параллелограмма в пять раз больше, чем градусная мера острого угла этого параллелограмма. Отношение градусных мер двух соседних углов этого параллелограмма равно
- В четырехугольнике мкрт середина отрезка мр является серединой отрезка кт
- Как написать хороший ответ?
- Срочно! В четырехугольнике MKPT середина отрезка MP является серединой отрезка КТ. Какому указанных числовых промежутков принадлежит сумма длин сторон МК и КР, если периметр четырехугольника равен 20? Варианты ответов: 1) (0;9) 2) (9;11) 3) (10,5;13) 4) (11:19)
- 📸 Видео
Видео:Вписанные четырехугольники. 9 класс.Скачать

В четырехугольнике мкрт середина отрезка мр является серединой отрезка кт
Вопрос по геометрии:
Срочно! В четырехугольнике MKPT середина отрезка MP является серединой отрезка КТ. Какому указанных числовых промежутков принадлежит сумма длин сторон МК и КР, если периметр четырехугольника равен 20?
Варианты ответов:
1) (0;9) 2) (9;11) 3) (10,5;13) 4) (11:19)
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
ДАНО: МКРТ — четырёхугольник ; КА = АТ ;
МА = АР ; Р mkpt = 20
1) Диагонали четырёхугольника МКРТ точкой пересечения делятся пополам =>
Значит, МКРТ — параллелограмм
2 × ( MK + KP ) = 20
Значит, МК + КР = 10
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Срочно! В четырехугольнике MKPT середина отрезка MP является серединой отрезка КТ. Какому указанных числовых промежутков принадлежит сумма длин сторон МК и КР, если периметр четырехугольника равен 20? Варианты ответов: 1) (0;9) 2) (9;11) 3) (10,5;13) 4) (11:19)
Поделись вопросом в социальных сетях!
Если Вы не получили ответ на свой вопрос, то предлагаем воспользоваться поиском, чтобы найти похожие вопросы и ответы по предмету -> Геометрия. А если Вы знаете правильный ответ сами, то будем признательны если Вы ответите, воспользовавшись формой ниже.
📸 Видео
574. Точка М — середина отрезка АВ, концы которого лежат на сфере радиуса R с центром О. Найдите:Скачать

№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
3 правила для вписанного четырехугольника #shortsСкачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Описанные четырехугольники. 9 класс.Скачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать

Пропорциональные отрезки круга. 9 класс.Скачать

#58. Олимпиадная задача о четырехугольникеСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

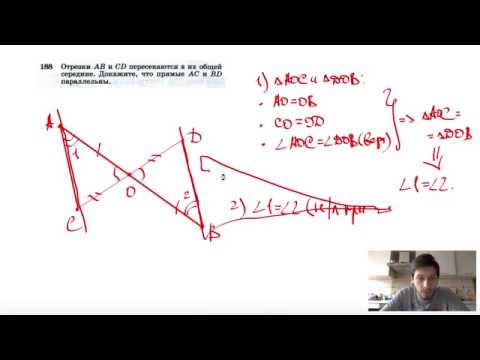
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать
ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

ЕГЭ Математика Задание 6#27935Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

№759 Дан произвольный четырехугольник MNPQ. Докажите, что:Скачать

