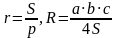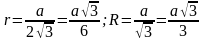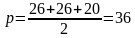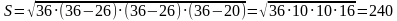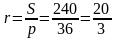Устные задачи по теме вписанные и описанные окружности

Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»

Тема: Решение задач по теме «Вписанная и описанная окружности»

Задачи: продолжить формирование навыков решения задач по теме.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.

Для любого треугольника:

Для равностороннего треугольника.

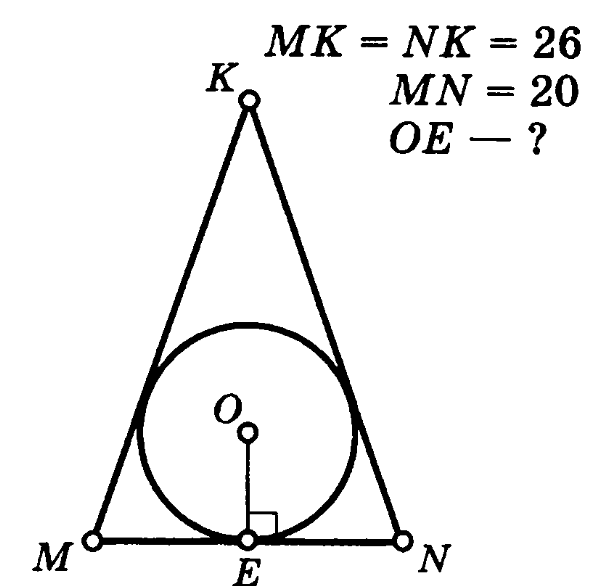
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.

Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 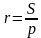, где р – полупериметр.

Ответ: .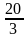

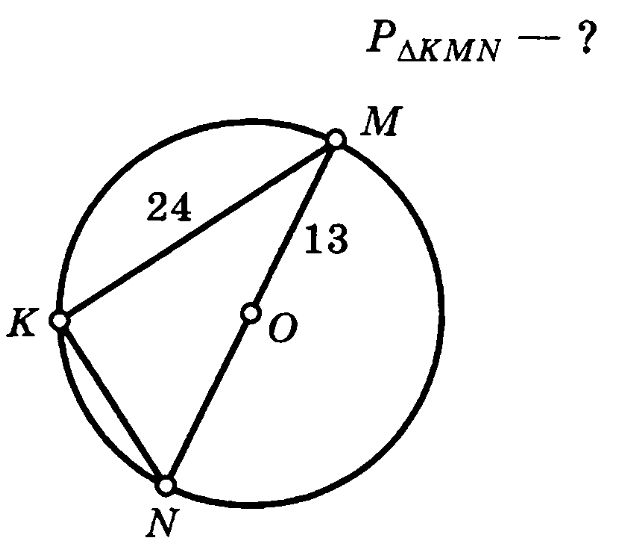
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.

Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.

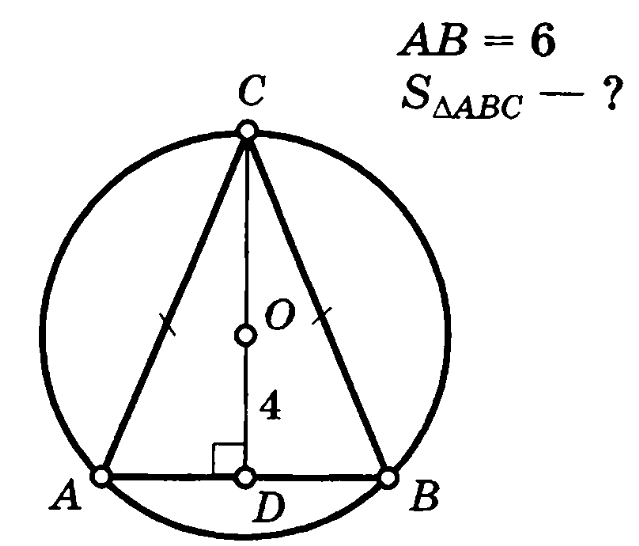
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.

Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.

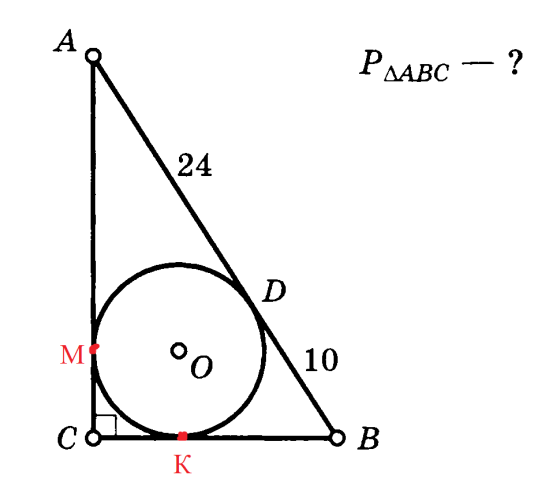
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.

Решение (краткое). DB=DK=10, AD=AM=24.

KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.

Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Устные задачи по теме вписанные и описанные окружности

Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.

значит,

Приведем другое решение.

Высота правильного треугольника равна 3 радиусам вписанной окружности, поэтому она равна 18.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Окружность, описанная вокруг трапеции, описана и вокруг треугольника Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:

откуда Тогда по теореме синусов:

Приведем другое решение (Р. А., СПб.).

Хорды AD, DC и CB равны, поэтому равны и стягиваемые ими дуги. Вписанный угол А равен 60°, он опирается на две из этих дуг и равен половине их суммы. Поэтому каждая из дуг равна 60°, их сумма равна 180°, а хорда АВ является диаметром. Отсюда получаем, что искомый радиус равен 6.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Решение задач по теме» Вписанная и описанная окружность» ( 8кл)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Решение задач по теме «Вписанная и описанная окружность»(8кл) МОБУ « Новочеркасская СОШ» Булдакова Л.П

Решить задачи 1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Решение Отрезки касательных равны, все они обозначены на чертеже. Найдем периметр: (5+3)*2 + 3*2 = 22.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Треугольник АСD египетский, значит, СD = 4. SABC=1/2(6*4) = 12 Воспользуемся формулой для вычисления радиуса.

В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.

Решение АВ=5 (это египетский треугольник). Р- полупериметр Р=6

Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Решение Пусть углы 1х, 2х, 3х. По условию около данного четырехугольника можно описать окружность А+С = D+B. Тогда угол D=2х. Сумма противоположных углов описанного четырехугольника 180. 1х+3х=180 (или 2х+2х=180) х=45 (1 часть) Угол D=90

Задача Два угла вписанного в окружность четырехугольника равны 82º и 58º. Найдите больший из оставшихся углов.

Решение Значит, — это углы соседние. Теперь воспользуемся свойством углов вписанного четырехугольника А+С = D+B =180. 1) 180 – 58 = 122 – это угол В. 2) 180 – 82 = 98 – это угол А. Больший из них – 122. Это не противолежащие углы, т.к. в описанном четырехугольнике их сумма равнялась бы 180 градусов.

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

дополнительные построения: центр О соединить с вершинами С и В (эти отрезки равны радиусу, т.е. 5). Получим два египетских треугольника ОHC и OFB. ОH=4, OF=3. Высота HF=7.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60º, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Решение Вписанный угол ВАD опирается на дугу DCB. дуга DCB=120, а дуга DC = 60. Три дуги стягивают равные хорды AD, DC, CB. Они равны 60. Тогда дуга AB= 180. а это означает, что АВ – диаметр, тогда радиус 12:2 = 6.

Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции

Решение 1) Средняя линия равна полусумме оснований. Тогда сумма оснований равна 10. 2) 22 – 10 = 12 это приходиться на боковые стороны. 3) 12:2 = 6, боковые стороны вписанной трапеции равны.

Интернет-ресурсы Книга: http://www.liveinternet.ru/users/4321745/post201324261/ Карандаш: http://allforchildren.ru/pictures/showimg/school5/school0519jpg.htm Линейка, циркуль, лекало: http://www.ineedsex.ru/main.php?g2_view=core.DownloadItem&g2_itemId=345&g2_serialNumber=2 Транспортир: http://knopka48.ru/images/detailed/1/26449_2.png

Автор шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново Сайт: http://pedsovet.su/

Краткое описание документа:

• Цели и задачи урока:Учить применять свойства вписанной и описанной окружности при решении задач;

• Развивать самостоятельность, логически мыслить и правильно выражать свои мысли;

В презентации представлены задачи по геометрии 8класса, по данной теме. 1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника

• Задача 2 Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Все задачи сопровождаются рисунками и решениями.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 510 568 материалов в базе

Другие материалы

• 24.04.2015
• 3502
• 8

• 24.04.2015
• 549
• 1

• 24.04.2015
• 745
• 2

• 24.04.2015
• 958
• 1

• 24.04.2015
• 3046
• 0

• 24.04.2015
• 9388
• 17

• 24.04.2015
• 3831
• 1

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 24.04.2015 33045
• PPTX 460.5 кбайт
• 614 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Булдакова Любовь Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 2 месяца
• Подписчики: 12
• Всего просмотров: 730339
• Всего материалов: 430

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

День памяти жертв холокоста включен в примерный план воспитательной работы

Время чтения: 1 минута

Школы Северной Осетии переведут на дистанционное обучение

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔍 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная и описанная окружности. ЗадачиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Вписанные и описанные окружности. С. р. 3 в1 9 классСкачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача №2.Скачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

Вписанные и описанные окружности. Геометрия 9 класс. Ключевая задача № 3.Скачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия 8 класс. Тема: "Вписанная и описанная окружности. Решение задач"Скачать

Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

ОПИСАННАЯ и ВПИСАННАЯ окружности. §21 геометрия 7 классСкачать

Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать