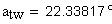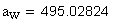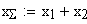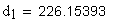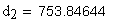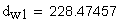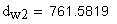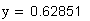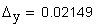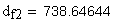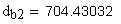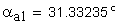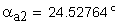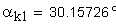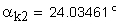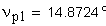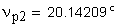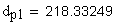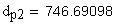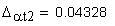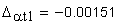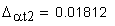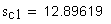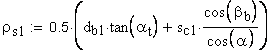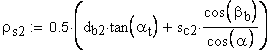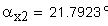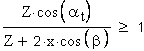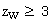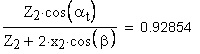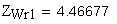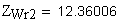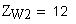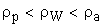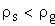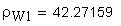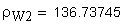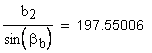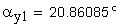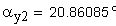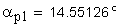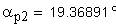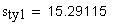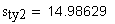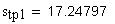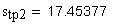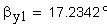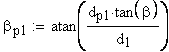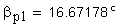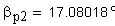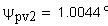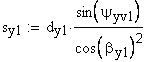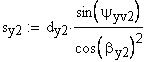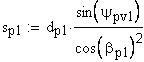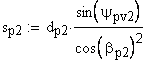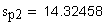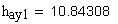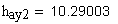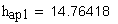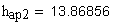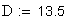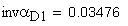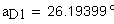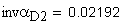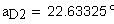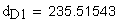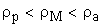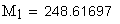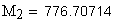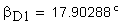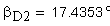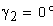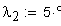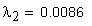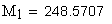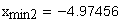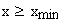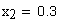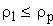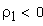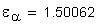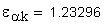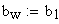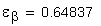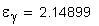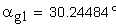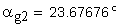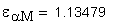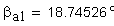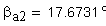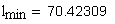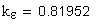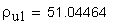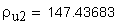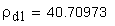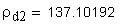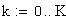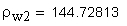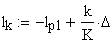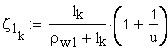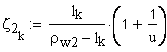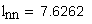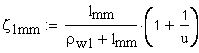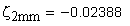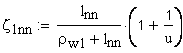Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z , а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r y разделить на z частей, каждая из которых называется окружным шагом p y .
где m y = p y / p = d y / z — модуль зацепления по окружности произвольного радиуса.
Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) — число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t — центральный угол соответствующий дуге p — окружному шагу по делительной окружности.
Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины — строчными буквами латинского алфавита, угловые — греческими буками; установлены индексы для величин :
по окружностям: делительной — без индекса, вершин — a , впадин — f , основная — b , начальная — w , нижних точек активных профилей колес — p , граничных точек — l ;
по сечениям: нормальное сечение — n , торцевое сечение — t , осевое сечение — x ;
относящихся к зуборезному инструменту — 0 .
Для параметров зубчатого колеса справедливы следующие соотношения




где a — угол профиля на делительной окружности,
a y — угол профиля на окружности произвольного радиуса.
Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом — вектором, проведенным в данную точку из центра колеса.
Шаг колеса делится на толщину зуба s y и ширину впадины e y . Толщина зуба s y — расстояние по дуге окружности r y между разноименными точками профилей зуба. Ширина впадины e y — расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.
На основной окружности a b => 0 и cos a b => 1 , тогда
В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:
нулевые s = e = p * m / 2 , D = 0;
положительные s > e , => D > 0;
отрицательные s D D — коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать
Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.
Толщина зуба колеса по окружности произвольного радиуса .
Толщина зуба по дуге делительной окружности
Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2
Подставляя в формулу угловой толщины эти зависимости, получим
Методы изготовления эвольвентных зубчатых колес .
Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:
метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму );
метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения — резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению , т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).
Из вариантов изготовления по способу копирования можно отметить:
Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие.
Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако при этом нельзя получить высокой прочности и твердости зубьев.
Из вариантов изготовления по способу огибания наибольшее распространение имеют:
Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности.
Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры.
Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью.
Понятие о исходном, исходном производящем и производящем контурах .
Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:
для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения — исходный контур;
для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения — исходный производящий контур.
По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:
угол главного профиля a = 20 ° ;
коэффициент высоты зуба h * a = 1 ;
коэффициент высоты ножки h * f = 1.25 ;
коэффициент граничной высоты h * l = 2 ;
коэффициент радиуса кривизны переходной кривой r * f =с * /(1-sin a )= 0.38 ;
коэффициент радиального зазора в паре исходных контуров с * = 0.25.
Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.
Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с * Ч m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий — в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура — проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.
Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.
Линия станочного зацепления — геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.
Смещение исходного производящего контура x*m — кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.
Уравнительное смещение D y*m — условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).
Окружность граничных точек r l — окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.
Основные размеры зубчатого колеса .
Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).
Радиус окружности вершин
Радиус окружности впадин
Толщина зуба по делительной окружности.
Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать
Виды зубчатых колес (Классификация по величине смещения) .
В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.
Подрезание и заострение зубчатого колеса .
Если при нарезании зубчатого колеса увеличивать смещение, то основная и делительная окружность не изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом участок эвольвенты, который используется для профиля зуба, увеличивает свой радиус кривизны и профильный угол. Толщина зуба по делительной окружности увеличивается , а по окружности вершин уменьшается.
На рис. 12.7 изображены два эвольвентных зуба для которых
Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого
При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения
улучшение, нормализация [s a /m ] = 0.2;
цианирование, азотирование [s a /m ] = 0.25. 0.3;
цементация [s a /m ] = 0.35. 0.4.
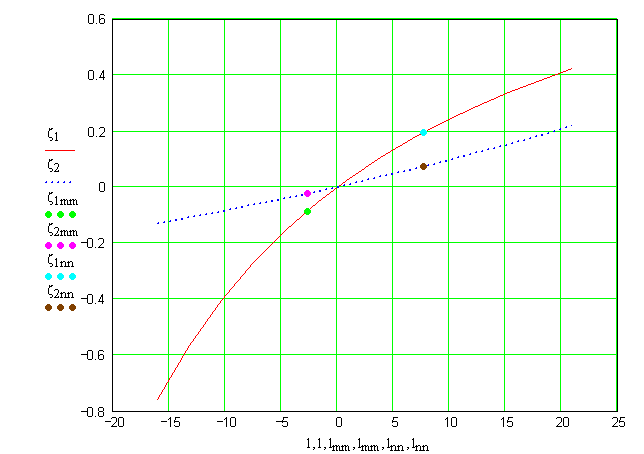
Подрезание эвольвентных зубьев в станочном зацеплении
В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B 1 . где точка B l определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка B l располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так
- Угол профиля на окружности вершин
- Расчет геометрических параметров зубчатой цилиндрической передачи (по ГОСТ 16532-70)
- Расчет основных геометрических параметров
- Расчет размеров для контроля номинальной поверхности зуба. Расчет размеров для контроля торцового профиля зуба.
- Дополнительный расчет при модификации головки исходного контура.
- Расчет размеров для контроля взаимного положения разноименных профилей зубьев. Расчет постоянной хорды и высоты до постоянной хорды.
- Расчет размеров для контроля взаимного положения одноименных
- Проверка качества зацепления по геометрическим показателям. Проверка отсутствия подрезания зуба
- 2.3. ЭВОЛЬВЕНТНЫЕ ЗУБЧАТЫЕ КОЛЕСА И ИХ ПАРАМЕТРЫ
- 📹 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Угол профиля на окружности вершин
Как выбрать и купить фрезерно-гравировальный станок с ЧПУ
Видео:Углы с вершиной внутри и вне окружности.Скачать

Расчет геометрических параметров зубчатой цилиндрической передачи (по ГОСТ 16532-70)
Исходные данные для расчета:
| Число зубьев шестерни ведущей | Z1:=27 |
| Число зубьев шестерни ведомой (колеса) — | Z2:=90 |
| Модуль,мм | m:=8 |
| Угол наклона зуба на делительной окружности | β:=17.2342*deg |
| Нормальный исходный контур | |
| Угол профиля | α:=20*deg |
| Коэффициент высоты головки | ha:=1 |
| Коэффициент граничной высоты | h1:=2 |
| Коэффициент радиального зазора (для стандартного контура) | c>=0.25 |
| Коэффициент высоты модификации головки | hg:=0.4 |
| Коэффициент глубины модификации головки | Δ:=0.008 |
| Коэффициент смещения (коррекции) у шестерни | x1:=0.35 |
| Коэффициент смещения (коррекции) у колеса | x2:=0.3 |
| Размер притупления продольной кромки вершины зубьев у шестерни, мм | k1:=1.5 |
| Размер притупления продольной кромки вершины зубьев у колеса, мм | k2:=1.5 |
| Ширина венца у шестерни, мм | b1:=55 |
| Ширина венца у колеса, мм | b2:=55 |
Параметры Mathcad: deg=0.01745, °=deg, TOL=1*10 -9
Расчет основных геометрических параметров
1. Делительное межосевое расстояние, мм
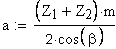
2. Угол профиля в торцовой плоскости.
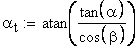
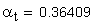
Расчет межосевого расстояния при заданных коэффициентах смещения
3. Угол зацепления в торцовой плоскости
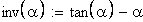
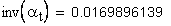
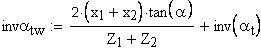
определение угла по его инволюте
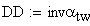
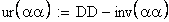
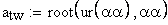
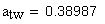
4. Межосевое расстояние, мм
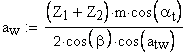
5. Коэффициент суммы смещений
Расчет диаметров зубчатых колес
6. Делительный диаметр, мм
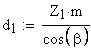
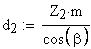
7. Передаточное число
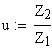
8. Начальный диаметр, мм
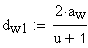
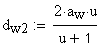
9. Коэффициент воспринимаемого смещения
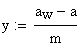
10.Коэффициент уравнительного смещения
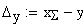
11.Диаметр вершин зубьев, мм
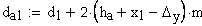
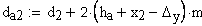
12.Диаметр впадин, мм
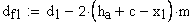
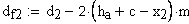
13.Диаметр притупления кромок вершин зубьев, мм
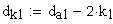
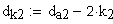
Расчет размеров для контроля номинальной поверхности зуба.
Расчет размеров для контроля торцового профиля зуба.
1. Основной диаметр, мм
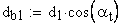
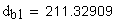
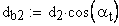
2. Угол профиля зуба в точке на окружности вершин, град.
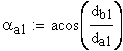
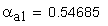
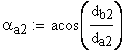
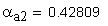
3. Угол профиля зуба в точке на окружности притупления кромок вершин, град.
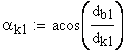
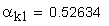
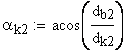
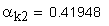
4. Радиус кривизны активного профиля зуба в нижней точке (без учета притупления), мм
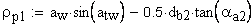

Примечание: формула справедлива, если верхняя точка активного профиля сопряженного зубчатого колеса совпадает с точкой профиля на окружности его вершин.
Если имеется притупление продольной кромки зуба, то вместо a1 и a2 следует подставлять соответственно ak1 и ak2
5. Угол развернутости активного профиля зуба в нижней точке
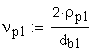
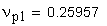
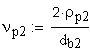
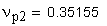
6. Диаметр окружности нижних точек активных профилей зубьев, мм
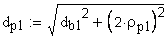
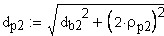
Расчет размера для контроля контактной линии поверхности зуба.
7. Основной угол наклона
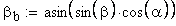
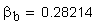
Дополнительный расчет при модификации головки исходного контура.
1. Радиус кривизны профиля зуба в начальной точке модификации головки, мм.
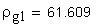
2. Угол развернутости профиля зуба, соответствующий начальной точке модификации головки.
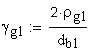
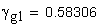
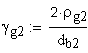
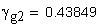
3. Диаметр окружности модификации головок зубьев, мм.
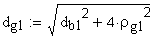
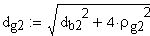
4. Угол линии модификации головки торцового исходного контура в начальной точке модификации.
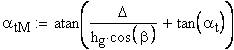
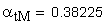
5. Диаметр основной окружности эвольвенты, являющейся линией модификации головки зуба, мм.
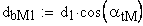
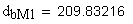
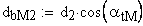
6. Нормальная глубина модификации торцового профиля головки зуба, мм.
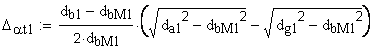
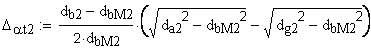
Если имеется притупление продольной кромки зуба, в выше приведенных формулах (6) следует подставить вместо da — dk
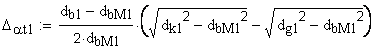
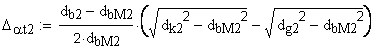
Примечание: формулы 4, 5, 6 справедливы, если линия модификации головки исходного контура — прямая.
Расчет размеров для контроля взаимного положения разноименных профилей зубьев.
Расчет постоянной хорды и высоты до постоянной хорды.
1. Постоянная хорда, мм
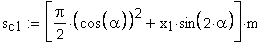
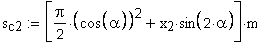
Должно выполняться условие
2. Радиус кривизны разноименных профилей зуба в точках, определяющих постоянную хорду, мм:
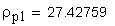
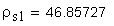
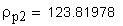
Указанное выше условие выполняется.
3. Высота до постоянной хорды, мм
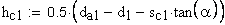
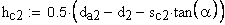
Расчет длины общей нормали.
4. Угол профиля в точке на концентрической окружности диаметра dx=d+2xm, град.

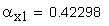

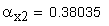
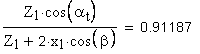
5. Расчетное число зубьев в длине общей нормали
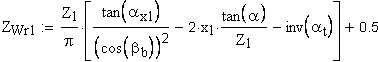
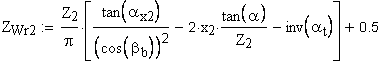
6. Длина общей нормали, мм
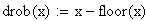
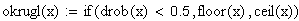
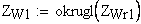
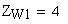
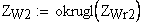
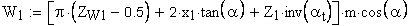
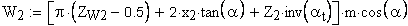
Должно выполняться условие:
При модификации головки должно выполняться дополнительное условие:
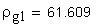
7. Радиус кривизны разноименных профилей зубьев в точках, определяющих длину общей нормали, мм
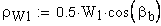
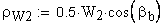
8. Радиус кривизны профиля зуба в точке на окружности вершин, мм
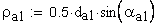
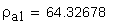
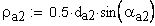
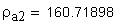
Указанное выше условие выполняется.
Если условие левой части неравенства не выполняется, следует пересчитать значение W при увеличенном значении Zw. Если условие правой части неравенства не выполняется, следует пересчитать W при уменьшенном значении Zw.
Для косозубых зубчатых колес должно выполняться дополнительное условие:
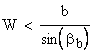
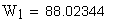
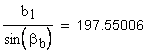
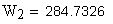
Расчет толщины по хорде и высоты до хорды.
9. Угол профиля в точке на концентрической окружности заданного диаметра dy,
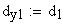

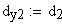



10. Окружная толщина зуба на заданном диаметре dy,
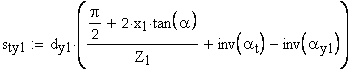
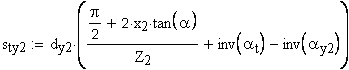
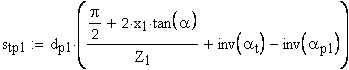
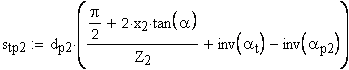
11. Угол наклона линии зуба соосной цилиндрической поверхности диаметра dy,
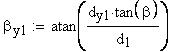
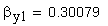
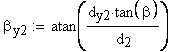
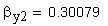
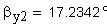
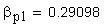
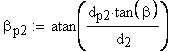
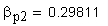
12. Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра , град
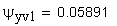
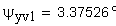
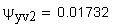
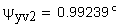
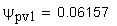
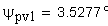
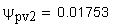
13. Толщина по хорде, мм
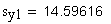
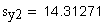
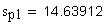
14. Высота до хорды, мм
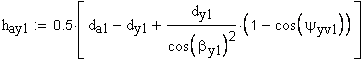
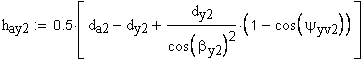
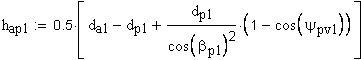
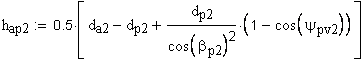
Расчет размера по роликам (шарикам).
15. Диаметр ролика (шарика), мм.
при a=20 град. рекомендуется
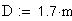
16. Угол профиля на концентрической окружности зубчатого колеса, проходящей через центр шарика
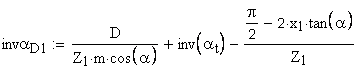
определение угла по его инволюте
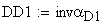
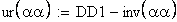
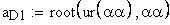
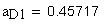
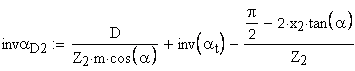
определение угла по его инволюте
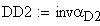
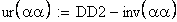
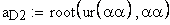
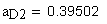
17. Диаметр концентрической окружности зубчатого колеса, проходящей через центр шарика, мм


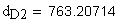
Должно выполняться условие:
18. Радиус кривизны разноименных профилей зубьев в точках контакта поверхности ролика (шарика) с главными поверхностями зубьев, мм
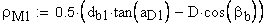
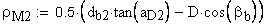
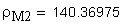
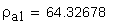
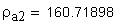
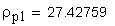
Указанное выше условие выполняется.
Если имеется притупление продольной кромки зуба, в неравенство вместо 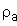
При модификации головки в неравенство вместо 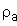
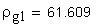
19. Размер по роликам (шарикам), мм
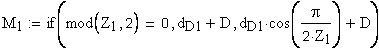
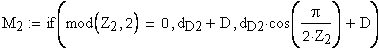
Должны выполняться условия:
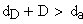
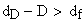
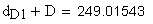
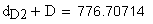
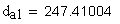
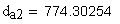
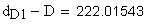
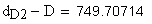
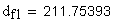
Указанные выше условия выполняются.
20. Минимальный размер по роликам (шарикам) косозубых зубчатых колес с нечетным числом зубьев, а также с четным числом зубьев при b>45° , мм
Угол наклона зуба на окружности, проходящей через центры шариков
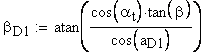
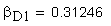
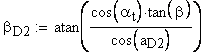
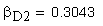
Вычисление значения угла γ
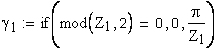
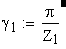
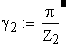
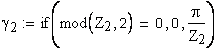
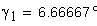
Вычисление значения угла λ
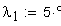
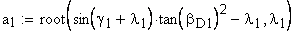
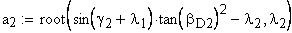
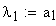
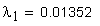
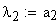


Расчет нормальной толщины зубчатого колеса.
21. Нормальная толщина зуба, мм
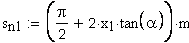
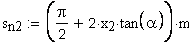
Расчет размеров для контроля взаимного положения одноименных
1. Шаг зацепления, мм
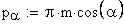
2. Осевой шаг зубьев, мм
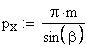
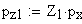
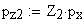
Проверка качества зацепления по геометрическим показателям.
Проверка отсутствия подрезания зуба
1. Коэффициент наименьшего смещения
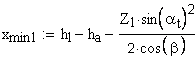
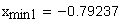
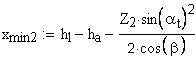
подрезание зуба исходной производящей рейкой отсутствует
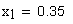
Проверка отсутствия интерференции зубьев
2. Радиус кривизны в граничной точке профиля зуба, мм


интерференция зубьев отсутствует
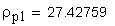
При подрезании зубьев
Проверка коэффициента перекрытия
3. Коэффициент торцового перекрытия
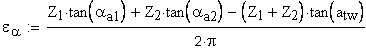
При наличии притупления продольной кромки вершин зубьев
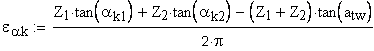
4. Коэффициент осевого перекрытия -для косозубых передач
рабочая ширина венца
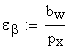
5. Коэффициент перекрытия — для косозубых передач
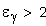
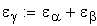
Дополнительный расчет при модификации головки исходного контура
6. Угол профиля зуба в начальной точке модификации головки
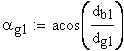
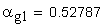
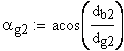
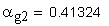
7. Часть коэффициента торцового перекрытия, определяемая участками торцовых профилей зубьев, совпадающих с главными профилями

сравнение величин радиусов:
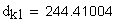
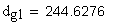
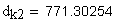
Проверка нормальной толщины на поверхности вершин
(без учета притупления кромок вершин зубьев)
8. Угол наклона линии вершины зуба
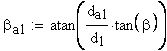
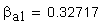
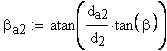
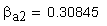
9. Нормальная толщина на поверхности вершин, мм
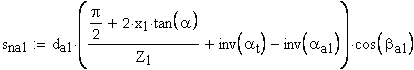
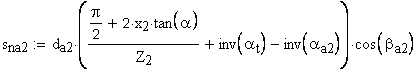
Рекомендуется при поверхностном упрочнении зубьев
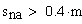
Рекомендуемое условие выполняется
1. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии. ГОСТ 16532-70.
2. Зубчатые передачи: Справочник / Е.Г. Гинзбург, Н.Ф. Голованов и др. Под общ. ред. Е.Г. Гинзбурга 2-е изд., перераб. и доп. _- Л.: Машиностроение, 1980. — 416 с.
для косозубых передач:
средняя суммарная длина контактных линий
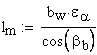
наименьшая суммарная длина контактных линий
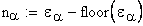
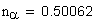
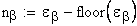
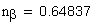

коэффициент среднего изменения суммарной длины контактных линий
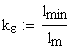
для прямозубых передач:
радиус кривизны профиля зуба в верхней граничной точке однопарного зацепления
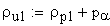
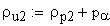
радиус кривизны профиля зуба в нижней граничной точке однопарного зацепления
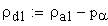
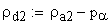
Расчет некоторых качественных показателей передачи
расчет удельных (относительных) скольжений
радиусы кривизны профилей зубьев в полюсе зацепления (в торцовом сечении)

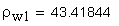
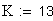

длина линии зацепления
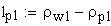
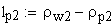
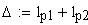
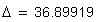
удельное скольжение профилей зубьев
длина линии зацепления в точке начала однопарного зацепления (в алгебраическом смысле)
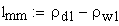
длина линии зацепления в точке конца однопарного зацепления
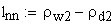
удельное скольжение профилей зубьев в точке начала однопарного зацепления
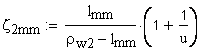
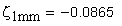
удельное скольжение профилей зубьев в точке конца однопарного зацепления
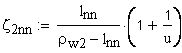
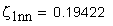
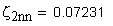
Расчет приведенного радиуса кривизны профилей зубьев
Видео:Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

2.3. ЭВОЛЬВЕНТНЫЕ ЗУБЧАТЫЕ КОЛЕСА И ИХ ПАРАМЕТРЫ
Рисунок 3. Параметры эвольвентного зубчатого колеса.
К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.
Виды модулей: делительный, основной, начальный.
Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.
Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.
Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения
Делительная окружность делит зуб на головку и ножку.
Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.
Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.
Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.
Сумма высот головки ha и ножки hf соответствует высоте зубьев h:
Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.
Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.
Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.
Коэффициент уравнительного смещения Δу:
Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.
Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу
Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев
Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба
S = 0,5 · ρ + 2 · х · m · tg α
Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев
Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.
Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.
Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра
📹 Видео
ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

ЕГЭ МАТЕМАТИКА (профиль) | Окружность и углы в окружностиСкачать

Ответы на вопросы по листу №3 ТММ (часть 2/5)Скачать

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.Скачать

Углы, вписанные в окружность. 9 класс.Скачать

❓ Угол между секущими (вне окружности)Скачать

Решение задач на тему центральные и вписанные углы.Скачать

Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противопСкачать
Вписанные углы в окружностиСкачать

Углы, связанные с окружностьюСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Найдите УГОЛ. Находим угол шестиугольной полки.Скачать

Задача № 27933 ЕГЭ по математике. Урок 147Скачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Найти число вершин 3 задание проф. ЕГЭ. по математикеСкачать