 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- Угол между секущими
- Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности
- Это полезно
- 🌟 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:❓ Угол между секущими (вне окружности)Скачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Угол между хордой и касательной. 9 класс.Скачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Углы с вершинами внутри и вне кругаСкачать  Угол между секущимиУгол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Для треугольника APN ∠ANC — внешний угол при вершине N. Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним, ∠ANC — вписанный угол, опирающийся на дугу AC, ∠PAN — вписанный угол, опирающийся на дугу MN. Так как вписанный угол равен половине дуги, на которую он опирается, то Видео:Угол между секущимиСкачать 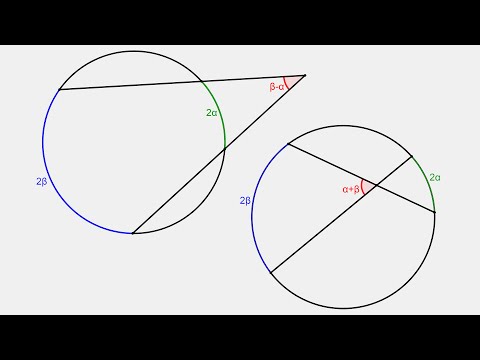 Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружностиПусть – угол между секущими МВ и МD. Докажем, что Угол DAB – вписанный. Его величина равна половине угловой величины дуги ВD. Угол АDС – вписанный. Его величина равна половине угловой величины дуги АС. Поскольку – внешний угол треугольника МАD, . Отсюда Видео:11 класс, 42 урок, Углы с вершинами внутри и вне кругаСкачать  Это полезноУзнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили. Наш онлайн-курс по Физике Все темы ЕГЭ с нуля Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале! Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали. Мы обязательно ответим! Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике. Результат будет выше, если готовиться по отработанной методике. У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей. 🌟 ВидеоМатематика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Угол с вершиной вне кругаСкачать 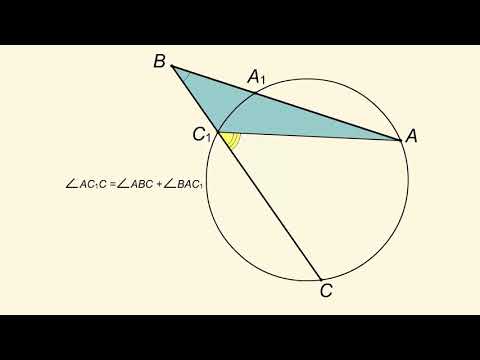 ОГЭ Задание 25 Угол между секущимиСкачать  Окружность..Угол между произвольными хордами.Скачать  Угол между секущими к окружностиСкачать  Углы, связанные с окружностьюСкачать  Секретная теорема из учебника геометрииСкачать  Углы, связанные с окружностьюСкачать  8 класс. Геометрия. Углы, образованные хордами, секущими и касательнымиСкачать 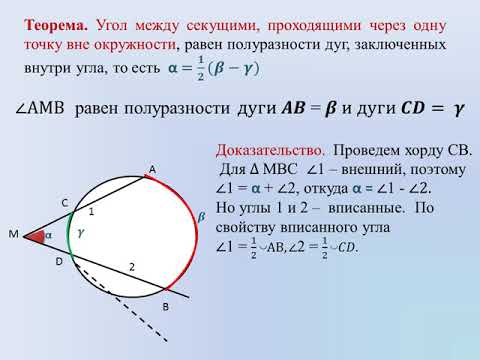 11 класс, 40 урок, Угол между касательной и хордойСкачать  Теоремы об отрезках, связанных с окружностью. Урок 22. Геометрия 11 классСкачать  Углы между хордами, касательными и секущими | Геометрия 8-9 классыСкачать  Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать  |



































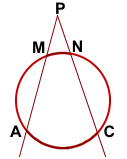

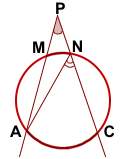 Проведём хорду AN.
Проведём хорду AN.







