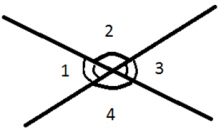
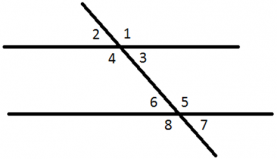
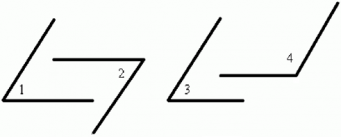Углы между параллельными прямыми теорема (2 видео)

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Содержание

Геометрия. 7 класс
51. Планиметрия Читать 0 мин.
51.65. Углы и параллельные прямые
📽️ Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия. 7 класс

Конспект урока

Свойства параллельных прямых

Перечень рассматриваемых вопросов:

Углы, образованные при пересечении двух прямых секущей.
Доказательство свойств параллельных прямых и их применение при решении задач.
Формулирование теоремы об углах с соответственно параллельными сторонами.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Утверждение, обратное данной теореме– это утверждение, в котором условие является заключением теоремы, а заключение – условием теоремы.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее мы узнали и научились применять признаки параллельности прямых.

Рассмотрим утверждения, обратные к теоремам, выражающим признаки параллельности двух прямых.

В любой теореме есть две части: условие (это то, что дано)и заключение (это то, что требуется доказать).

Утверждением, обратным данному, называется утверждение, в котором условием является заключение, а заключением – условие.

Итак, вспомним один из признаков параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы, образованные этими прямыми и секущей, равны (это условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.

Если две параллельные прямые пересечены секущей, то накрест лежащие углы,образованные этими прямыми и секущей,равны.

∠1 и ∠2 – накрест лежащие.

Доказательство:( метод от противного):

Отложим ∠PMN =∠2 (накрест лежащие) → МР║b→ через точку М проходит 2 параллельные прямые прямой b (МР║b– доказательство;a║b– условие).→∠1=∠2.

Это противоречит теореме о единственности прямой параллельной данной и проходящей через точку.

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

С пересекает а, значит, и пересекает параллельную ей прямую b(по следствию из аксиомы параллельных прямых).→ с – секущая к прямым а и b→∠1 = ∠2 = 90° (по только что доказанному свойству параллельных прямых).→ с ┴ b.

Что и требовалось доказать.

Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей соответственные углы равны(это условие), то прямые параллельны(заключение).

Сформулируем и докажем обратное утверждение

Если две параллельные прямые пересечены секущей, то соответственные углы, образованные этими прямыми и секущей, равны.

Дано:

Доказать:

По условию a║b→∠1 = ∠3 (накрест лежащие углы). → ∠2 = ∠3 (вертикальные углы).

Значит, ∠1 = ∠2, что и требовалось доказать.

Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей сумма односторонних углов, образованных этими прямыми и секущей, равна 180° (условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.

Если две параллельные прямые пересечены секущей, то сумма односторонних углов, образованных этими прямыми и секущей, равна 180°.

Дано:a║b,

Доказать:

По условию a║b→∠1=∠2 ‑соответственные углы, (в силу предыдущей теоремы).

∠2+∠4=180° (по свойству смежных углов).

→ ∠1+∠4= 180°,что и требовалось доказать.

Материал для углубленного изучения темы.

Задача на доказательство.

Прямая m пересекает параллельные прямые а и b в точках А и В. Прямая р, проходящая через середину отрезка АВ, точку О, пересекает прямые а и b в точках С и D.

Докажем, что ОС=ОD.

По условию дано: а ║b, рՈа= А, рՈb = В, mՈа = D, mՈb = C.

Доказать: ОС = ОD.

Доказательство: рассмотрим, образовавшиеся при построении, треугольники AOD и BOC. Они равны по 2 признаку равенства треугольников, т.к. АО=ВО (О– середина отрезка АВ по условию); ∠1=∠2(накрест лежащие углы); ∠3=∠4 (вертикальные углы). →Все элементы равных треугольников соответственно равны → ОС=ОD. Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1. Три прямых а,р,с пересечены прямой k, при этом образуются соответственные углы: ∠1= 30°,∠2 = 40°,∠3= 30°,как показано на рисунке. Какие из прямых параллельны?

На рисунке изображены прямые а, р, с, которые пересечены секущей k. При этом углы 1,2,3 соответственные. По условию: ∠3= ∠1= 30°,∠2 ≠ ∠1,∠2 ≠ ∠3.

Следовательно, прямые а и р параллельные, прямые а и с, р и с не параллельные(по свойствам параллельных прямых).

2. На рисунке прямые а║b, при этомMO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ, если сумма углов в треугольнике равна 180°?

По условию а║b→∠М+∠Е=180° (по теореме о параллельных прямых об односторонних углах). Т.к. MO и ЕО – биссектрисы углов М и Е →∠М = 2∠ОМЕ,

∠М+∠Е =2∠ОМЕ +2∠МЕО =180°.

По условию сумма углов в треугольнике равна 180° → в ∆МОЕ.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

51. Планиметрия Читать 0 мин.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

51.65. Углы и параллельные прямые

Взаимное расположение прямых:

Прямые пересекаются, у них есть одна общая точка.
Прямые не пересекаются, у них нет общих точек. Такие прямые называются параллельными.

При пересечении двух прямых образуются вертикальные и смежные углы.

Вертикальные углы — равны.

Сумма смежных углов равна 180°.

Параллельные прямые

Прямые называются параллельными, если они не пересекаются, сколько бы их не продолжать.

О параллельных прямых:

Если одна из пары параллельных прямых параллельна третьей прямой, то все прямые параллельны между собой.
На плоскости через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

При пересечении двух параллельных прямых секущей образуются следующие углы:

внутренние накрест лежащие (4 и 5, 3 и 6) — попарно равны;
внешние накрест лежащие (1 и 8, 2 и 7) — попарно равны;
соответственные (1 и 5, 2 и 6, 3 и 7, 4 и 8) — попарно равны;
внутренние односторонние (3 и 5, 4 и 6) — сумма таких углов равна 180°;
внешние односторонние (1 и 7, 2 и 8) — сумма таких углов равна 180°.

Часто для использования свойств углов, полученных при пересечении двух параллельных прямых секущей, необходимо применять дополнительные построения.

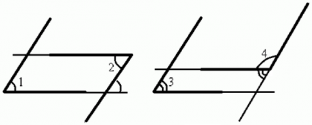
Пример: Даны углы с попарно параллельными сторонами. Что можно сказать об углах 1 и 2? Что можно сказать об углах 3 и 4?

Продолжим стороны углов до пересечения:

Получаем, что углы 1 и 2 равны, т. к. являются накрест лежащими при параллельных прямых.

Сумма углов 3 и 4 равна 180°, т. к. они являются односторонними при параллельных прямых.

Теорема Фалеса: При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки (образуются подобные треугольники).