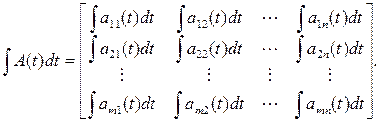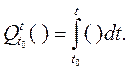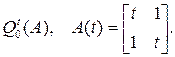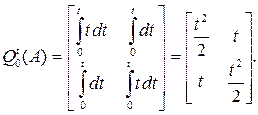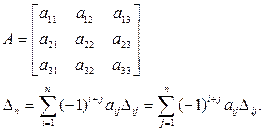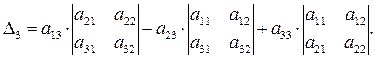Дифференцирование матрицы по вектору (5 видео)

Векторное дифференцирование

В дальнейшем в различных главах будет использовано векторное дифференцирование, которое позволяет использовать более компактную и наглядную запись. Поэтому в этом параграфе кратко рассмотрим определения и свойства векторного дифференцирования (символ *= f обозначает равенство по определению).

1) Производная вектора х = (х Х2 . х_п) Т по скаляру t:

2) Производная скалярной функции 5 = s (х) по вектору х = = (х Х2 . х_п) Т :

3) Производная векторной функции f (х) (f = (Д . /_п) т ) по вектору х = (si Х2 . х_п) Т :

Используя приведенные определения и обычные правила дифференцирования, можно получить следующие правила векторного дифференцирования.

1°. Производная скалярного произведения по скаляру t:

Если у = х, то имеем

2°. Производная произведения матрицы и вектора по скаляру t:

А — (т х п)-матрица, зависящая от t.

3°. Производная скалярного произведения по вектору х =

Если у = z, то имеем

4°. Производная квадратичной формы по вектору х = = (Xj Х2 • • • &п) •

Q — симметрическг^я (тг х п)-матрица, не зависящей от х.

5°. Производная сложной векторной функции по скаляру t:

Видео:Семинар 2. Матрично - векторное дифференцирование. МФТИ. 2022Скачать

Дифференцирование матрицы по вектору

2.3. МАТРИЧНОЕ ДИФФЕРЕНЦИРОВАНИЕ

Аппарат векторно-матричного исчисления не приспособлен для манипуляций, целью которых является нахождение интегралов и производных от функций матричного аргумента. Недостаток аксиоматики в этом направлении известен, памятная табличка формул матричного дифференцирования нет-нет, да встречается в работах – в приложении или в первой главе. При внимательном отношении табличкам свойственно разрастаться в таблицы. Чтобы от них избавиться, надо предложить систему формального дифференцирования, позволяющую находить результат, желательно, по простым правилам.

Попытаемся привести некоторые лежащие на поверхности соображения на этот счет. Начнем с формального определения.

Понятие производной скалярной функции по матрице уже устоялось. Это матрица, элементами которой являются частные производные функции по каждому элементу. Таков, например, градиент. Производная матрицы по скалярному аргументу образуется матрицей производных каждого ее элемента по одному и тому же аргументу. Расширяя эти толкования, придем к определению, согласно которому производная матрицы по матричному аргументу представляет собой блочную матрицу, в которой каждый блок включает производную дифференцируемой матричной функции по скалярному аргументу – элементу матричного аргумента.

Для того, чтобы лаконично записывать результаты формальных матричных действий, придется ввести пару относительно новых обозначений. Первое касается векторизации A ↑ матрицы, когда ее элементы строчка за строчкой последовательно слагаются в столбец. Второе обозначение для блочно-диагональной структуризации существует , но есть желание иногда писать его короче, просто . Количество повторений блоков A на диагонали, как и многое другое в матричной алгебре, остается за бортом, что не всегда правильно. Можно предложить другой эквивалент обозначения этой операции, например, такой: <A, n>.

Указанные операции обладают рядом почти очевидных свойств, например, (x T ) ↑ =x и .

Отметим попутно у матричного дифференцирования коммутирующее знак транспонирования качество, оказывается что

Любопытно и просто выглядят производные векторных функций по векторному аргументу, существует несколько вариантов, в частности, такие

Производная произведения двух матриц по матричному же аргументу размера nxm трансформируется к виду

В случае скалярного аргумента формула становится тривиальной. Для часто встречаемого векторного аргумента первая диагонализация отмирает, поскольку m = 1. Символ n можно подразумевать.

В качестве демонстрации силы разделаемся с квадратичной формой, которую при ином подходе приходится дифференцировать поэлементно, а потом собирать ответ, как картинку из кубиков, итак

Метод наименьших квадратов связан с поиском сложной производной от матрицы, имеем

Так, в одну строчку, выводятся формулы, под которые бронируется место в приложениях. Идее нужно выдержать испытание временем, пусть пока эстетическая сторона дела доставит удовольствие.

В теоретической механике и теории поля есть свой набор дифференциальных операторов, например, ротор и дивергенция.

Вспоминая правило буравчика, незаменимое в исследовании электромагнитных явлений, отметим, что оно описывает поворот на 90 градусов. Механики для этой цели придумали векторное произведение y = ω⊗x, пасынка матричного исчисления: ортогональные матрицы закрывают потребности в обеспечении поворотов. Среди них есть конструкции кососимметрические, отвечающие за прямой угол. Поворот с дополнительным растяжением не меняет вида матрицы, так что для векторного произведения нетрудно подыскать матричный аналог y = Wx, где

Смешанное произведение векторов z(ω⊗x) выливается в привычную запись билинейной формы z T Wx.

Попробуем найти матричную интерпретацию дифференциальных операторов. Понять их содержание неспециалисту нелегко, между тем, они используются в уравнениях Максвелла, играющих фундаментальную роль в науке. Эти уравнения дали жизнь теории относительности и навели Шредингера на объяснение дискретной природы процессов микромира. Матричная аналогия способна внести некоторое более ясное видение сложных вещей. Физическое пространство, в котором распространяется электромагнитная волна, трехмерно. Изменения полей в нем оцениваются частными производными напряженности вдоль трех пространственных направлений.

Оператором Гамильтона ∇ называют собрание операций взятия частных производных по трем направлениям физического мира. Применительно к скалярной функции трех координат этот оператор порождает градиент. Что касается векторной функции θ(x), наделенной в каждой точке x пространства величиной и направлением, то количество частных производных расширяется до девяти, собираемых в матрицу dθ T /dx. Дивергенция представляет собой след этой матрицы, т.е. сумму трех обусловленных индексами координатных осей производных div θ(x) = trace dθ T /dx.

Дивергенция носит все признаки скалярного произведения векторов ∇ и θ(x). Ротор, напротив, формально определяется как векторное произведение, т.е. rot θ(x) = ∇⊗θ(x). Такого сорта дефиниции дают скудную пищу воображению. Недаром с уравнениями Максвелла пришлось поработать нескольким математикам, только чтобы их разъяснить [6].

Фарадей находил силовые лини магнитного поля, насыпая металлические опилки на лист бумаги и поднося его к полюсу магнита.

Попробуем воспользоваться его методом. Лучи силовых линий в чем-то подобны градиенту квадратичной функции f(x)=0.5x T Ax.

Фазовые портреты линейных динамических систем, описывающих движения вдоль градиента , являются удобным руководством для постижения топологических особенностей векторных полей. Дивергенция вектора градиента представляет собой сумму вторых частных производных (это действие приписывают оператору Лапласа Δ) квадратичной функции, в данном случае она равна сумме диагональных элементов матрицы A. Не менее просто определить у такого поля ротор. Он составлен из разностей внедиагональных элементов A. Полям с нулевым ротором отвечают диагональные матрицы простыми собственными значениями.

Полям с нулевой дивергенцией отвечаю матрицы с чисто мнимыми собственными значениями. Среди матриц c нулевой диагональю отметим кососимметрические. Квадратичную форму с их помощью не построишь, градиент не способен на такие фокусы, как замыкание. Но динамическая система ẋ=Ax существует. В отсутствии монополей силовые линии электрического и магнитного полей замкнуты, не имеют ни начала, ни конца. Такие траектории прочерчивают частицы несжимаемой жидкости, подкрученной в ванне без слива. Задание нулевых дивергенций электрического и магнитного полей сродни заданию начальных условий, определяющих пространственные характеристики силовых линий.

Электромагнитное поле распространяется благодаря самоиндукции. Для ее описания и потребовался ротор или вихрь – завиток (curl), как поэтично назвал его склонный к стихотворным опусам Джеймс Клерк Максвелл, имевший, к тому же, привычку подписываться формулой dp/dt=JCM. В безвихревом гравитационном поле книга падает на пол прямо, не совершая утиные движения сорванного осенью с ветки листка. Уравнение электростатического поля констатирует, что ротор его напряженности равен нулю. Такое поле развернуто и скручивается в пространстве, если происходят изменения во времени поля магнитного. И наоборот, магнитное поле скручивается под влиянием изменения во времени поля электрического.

Максвелл крест накрест приравнял (с точностью до коэффициентов) временные и вихревые пространственные производные напряженностей электрического и магнитного полей. Теорию ждало открытие. Коэффициенты уравнений можно установить из опыта с диэлектриками. Отсюда вычисляется скорость распространения электромагнитного излучения. Она оказалась равной скорости света, измеренной астрономами.

Видео:Матрицы и векторыСкачать

Дифференцирование матриц

Пусть A(t) – матрица (m x n), элементы которой a_ij есть дифференцируемые функции скалярной переменной t. Производная от матрицы A(t) по переменной t есть матрица, элементами которой являются :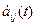

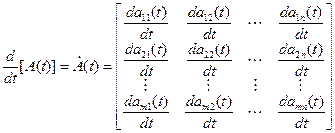
Производная от суммыдвух матриц равна сумме производных от этих матриц:

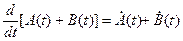
Производная от произведенияматриц:

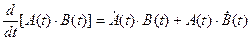
При этом должен сохраняться первоначальный порядок следования сомножителей произведения.

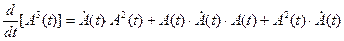
Интегрирование матриц

Интеграл от матрицы определяется как матрица, образованная из интегралов от элементов исходной матрицы. Следовательно,

Для обозначения интеграла от матрицы обычно используется символ Q=∫ ( )dt. Если оператор Q снабжен индексами (сверху t, а снизу t₀), то они указывают нижний и верхний пределы интегрирования:

Пример 4. Найти

Определители

Определители существуют только для квадратных матриц.

В общем случае используется разложение Лапласа определителя n порядка по элементам строки (столбца) на сумму n определителей (n–1) порядка.

Например, для n = 3:

Свойства определителей

1. Определитель равен единице, если матрица А– единичная.

2. Определитель равен нулю, либо если все элементы матрицы равны нулю, либо все элементы строки (или столбца) равны нулю, или равны между собой или пропорциональны элементы произвольных двух строк (или двух столбцов).

3. Величина определителя остается неизменной по модулю при перестановке местами его строк (или столбцов).

4. Знак определителя изменяется на противоположный при замени местами его двух строк (или столбцов).

5. Значение определителя умножается на постоянную k, если все элементы какой-либо его строки (столбца) умножаются на k.

6. Значение определителя не изменяется, если к какой-либо его строке (или столбцу) прибавить умноженные на k соответствующие элементы другой строки (или столбца).