Циркуляция вектора напряженности магнитного поля вдоль окружности

Видео:Лекция 2.3. Теорема о циркуляцииСкачать

Теорема о циркуляции вектора напряженности

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Теорема о циркуляции вектора напряженности электрического поля

Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($overline$), который определен как сила ($overline$), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:

Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:

где $overline$ — перемещение.

Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора $overline$- это работа, которую могут совершить силы Кулона, перемещая положительный заряд равный единице по контуру.

Учитывая, что $qne 0$, получим:

Теорема о циркуляции вектора напряжённости электростатического поля говорит о том, циркуляция $overline$ по замкнутому контуру равна нулю.

В дифференциальной форме теорему о циркуляции записывают как:

[rot overline=0 left(4right).]

Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.

Как следствие из теоремы о циркуляции $overline$: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.

Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Теорема о циркуляции вектора напряженности магнитного поля

Физическая величина ($overline$), являющаяся характеристикой магнитного поля, равная:

называется напряженностью магнитного поля. $overline$ — вектор магнитной индукции поля; $_0$ — магнитная постоянная; $<overline

>_m$- вектор намагниченности.

Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:

Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.

Циркуляция вектора напряженности в общем случае отлична от нуля, это означает, что магнитное поле — это вихревое поле, оно не является потенциальным.

Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.

Теорема о циркуляции вектора $overline$ исполняет роль, похожую на роль теоремы Гаусса для вектора напряженности электрического поля. Если имеется симметрия при распределении токов, то используя теорему о циркуляции $overline,$ находят саму напряженность магнитного поля.

Видео:теорема о циркуляцииСкачать

Примеры задач с решением

Задание. Определите, является ли потенциальным электрическое поле, которое задано уравнением: $overlineleft(x,yright)=Aleft(2xy overline+left(x^2-y^2right)overlineright).$

Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:

[rot overline=0 left(1.1right).]

следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:

Частные производные от $overline$ равны:

Подставляя (1.4) в (1.3), получаем, что

[rot overline=rot left[Aleft(2xy overline+left(x^2-y^2right)overlineright)right]=0.]

Ответ. Поле является потенциальным.

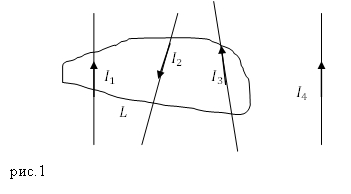
Задание. Какова циркуляция вектора напряженности магнитного поля для замкнутого контура $L$ (рис.1), если $I_1=5 A;; I_2=2 A;; I_3=10 A;; I_4=1 A?$

Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:

Контур $L$ охватывает три тока, следовательно:

Ответ. $ointlimits_L<overlinedoverline=13А .>$

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Теорема о циркуляции вектора напряженности магнитного поля. Расчет полей соленоида и тороида

Построим картину линий напряженности магнитного ноля вокруг бесконечного прямолинейного проводника с током (рис. 22.4). По аналогии с циркуляцией вектора напряженности электростатического поля (17.7) введем понятие циркуляции вектора напряженности магнитного

Для простоты сначала в качестве контура выберем окружность, совпадающую с одной из линий напряженности магнитного поля. В соответствии с формулой (22.12) напряженность на этой окружности является константой. А в соответствии с рис. 22.4 вектор напряженности направлен но касательной к окружности. Эти соображения позволяют вычислить циркуляцию:

Принцип суперпозиции магнитных полей и рассуждения, аналогичные предпринятым в разделе о циркуляции вектора напряженности электростатического поля, позволяют обобщить полученное выражение на несколько токов и произвольный контур:

Это и есть теорема о циркуляции вектора напряженности магнитного поля: циркуляция вектора напряженности магнитного поля по произвольному контуру равна алгебраической сумме токов, охватываемых контуром.

Теперь домножением обеих частей уравнения (22.18) на р₀ц получим теорему о циркуляции вектора магнитной индукции:

Искусство применения теоремы о циркуляции состоит в выборе удобного для расчета контура.

Применим теорему о циркуляции для вычисления напряженности магнитного поля длинного соленоида с током I. Соленоид — это провод, равномерно навитый на цилиндрический каркас (рис. 22.5). Будем считать, что диаметр каркаса много меньше его длины, а шаг плотной намотки (расстояние между витками) много меньше диаметра. При этих условиях поле внутри соленоида, как будет очевидно из результата, много больше поля вне соленоида и достаточно однородно (заметим, что поле вне соленоида можно определить по формуле для магнитного поля прямого тока (22.12)). Из соображений симметрии поле внутри соленоида направлено вдоль оси соленоида. Пусть плотность намотки витков (количество витков на единицу длины каркаса) равна п витков на метр.

В соответствии с рис 22.5 выберем прямоугольный контур, у которого малые (по сравнению с большими сторонами длиной /) стороны 2—3 и 4—1 в точке протыкания каркаса перпендикулярны каркасу, большая сторона 1—2 находится внутри каркаса, большая сторона 3—4 находится вне каркаса. В такой ситуации в циркуляции, состоящей из четырех интегралов по отрезкам, доминирует составляющая по отрезку 1—2. Составляющими по отрезкам 2—3 и 4—1 можно пренебречь вследствие малости отрезков. Составляющей по отрезку 3—4 можно пренебречь вследствие перпендикулярности (приблизительно) поля отрезку и малости этого поля. Внутрь контура попадает п! витков с током. Таким образом, циркуляция сводится к отрезку 1—2, но в соответствии с формулой (22.19) определяется полным током nil внутри контура:

Отметим, что это поле достаточно однородно по диаметру каркаса, ведь стороны 2—3 и 4— 1 малы лишь по сравнению с длиной каркаса, но могут быть сравнимы с диаметром каркаса и углубляться внутрь каркаса на любое расстояние.

Соответственно, магнитная индукция внутри длинного соленоида равна

Вычислим теперь магнитное иоле тороида. Тороид — это провод, навитый на тор (бублик). Его можно получить из соленоида, изогнув его в кольцевую катушку (рис. 22.6). Поле тороида похоже на поле соленоида, и линии напряженности тороида параллельны оси тороида. Покажем это, выбрав в качестве контура для вычисления циркуляции окружность радиуса г внутри тора с центром в центре тороида. По теореме о циркуляции для тороида с полным числом витков провода N

откуда магнитное поле внутри тороида

Если контур проходит вне тороида, то внутри него токи отсутствуют, т.е.

и поле из теоремы о циркуляции равно нулю. Таким образом, магнитное поле тороида локализовано внутри тороида и спадает по мере удаления от центра симметрии.

Если тороид тонкий и его радиус R

г много больше радиуса витка, то несложно получить, что поле внутри тороида (22.24) дается формулой, аналогичной формуле для поля соленоида (22.22):

Видео:Формула Стокса.ЦиркуляцияСкачать

Вектор напряженности магнитного поля

Для описания магнитного поля используются две его основные характеристики — индукция B → и напряженность H → . Эти величины связаны между собой. Рассмотрим, что такое напряженность магнитного поля, чему она равна, каков физический смысл этой величины.

Видео:Непосредственное вычисление циркуляцииСкачать

Напряженность магнитного поля

Напряженность магнитного поля — векторная физическая величина, в общем случае равная разности векторов индукции магнитного поля B → и намагниченности P m → .

Напряженность обозначается буквой Н → . Единица измерения напряженности магнитного поля в системе СИ — ампер на метр ( А м п е р м е т р ).

Формула напряженности магнитного поля:

Н → = 1 μ 0 B → — P m → .

Здесь коэффициент μ 0 — магнитная постоянная. μ 0 = 1 , 25663706 Н А 2 .

Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать

Физический смысл напряженности магнитного поля

Индукция магнитного поля — силовая характеристика. Индукция определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью.

Напряженность поля характеризует густоту силовых линий (линий магнитной индукции).

Физический смысл напряженности магнитного поля

В вакууме или при отсутствии среды, способной к намагничиванию (например, в воздухе) напряженность магнитного поля совпадает с магнитной индукцией с точностью до коэффициента μ 0 .

В средах, способных к намагничиванию (магнетиках) напряженность несет смысл как бы «внешнего поля». Она совпадает с вектором магнитной индукции, который был бы, если бы магнетика не было.

Видео:13. Магнитное поле. Введение. (русс яз)Скачать

Циркуляция вектора напряженности магнитного поля

Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля — своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.

Теорема о циркуляции магнитного поля

Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.

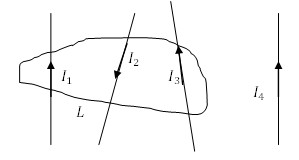
Определить циркуляцию вектора напряженности для замкнутого контура L .

I 1 = 5 A , I 2 = 2 A , I 3 = 10 A , I 4 = 1 A .

По теореме о циркуляции:

Рассматриваемый контур охватывает токи I 1 , I 2 , I 3 .

Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:

​​​​​ ∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .

Магнитное поле — вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.

🎬 Видео

Физика - Магнитное полеСкачать

Магниты. Магнитные свойства вещества. Диамагнетики, парамагнетики, ферромгнетикиСкачать

Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Билет №02 "Теорема Гаусса"Скачать

Теорема о циркуляции вектора Н.МагнетикСкачать

Урок 289. Магнитное поле в веществе. Магнитная проницаемость. Диа-, пара- и ферромагнетикиСкачать

Билет №17 "Магнитное поле в веществе"Скачать

ОГЭ. Физика. Определение плотности твердого телаСкачать

Циркуляция векторного поляСкачать

53. Теорема о циркуляции вектора индукцииСкачать

Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать