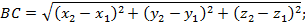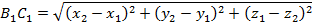Центральной симметрии прямая проходящая через центр симметрии отображается на параллельную ей прямую

Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а.

Пусть А ∈ а, построим отрезок ОА.

Продолжим ОА за точку О на расстояние ОА₁=АО. Получим точку А₁, симметричную А.

Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ₁=ОВ. Получим точку B₁, симметричную точке В.

Через А₁ и В₁ проведем прямую b. Рассмотрим ΔAОВ и ΔА₁ОВ₁⋅AО=А₁О, ВО=ОВ₁, ΔАОВ=ΔА₁ОВ₁ как вертикальные, следовательно, ΔAОВ=ΔА₁ОВ₁.

Тогда, ∠1=∠2 и а || b.

б) Пусть А ∈ а. Симметричная ей точка А₁ тоже принадлежит прямой а; АО=ОА₁.

Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №479
к главе «Глава V. Метод координат в пространстве. § 3. Движения».

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Тема: Центральная и зеркальная симметрия

Выполнила ученица 11 А класса Ковалева Дарья

Учитель Багирян Нонна Александровна

· определение и основные свойства

· фигуры, обладающие центральной симметрией

· применение в жизни

· определение и построение

· фигуры, обладающие зеркальной симметрией

· зеркальная симметрия в реальной жизни

Центральной симметрией называют преобразование пространства относительно точки A , переводящее точку X в такую точку X′, что A — середина отрезка XX′. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре.Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

· Центральная симметрия является движением;

· Любая прямая при центральной симметрии преобразуется в прямую. Причем, прямая, проходящая через центр, преобразуется в себя. Прямая, не проходящая через центр, преобразуется в параллельную ей прямую. (доказано в задаче 2)

· Центральная симметрия сохраняет расстояния между точками.

· Центральная симметрия переводит отрезки в отрезки, лучи в лучи.

Докажем, что центральная симметрия является движением.

Обозначим буквой O центр симметрии и введем в прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек M (x; y; z) и M₁ (x₁; y₁; z₁), симметричных относительно точки О.

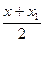
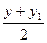
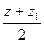
Если точка М не совпадает с центром О, то О – середина отрезка ММ₁. По формулам координат середины отрезка получаем = 0, = 0, =0, откуда x₁ = -x, y₁= -y, z₁ = -z.

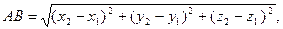
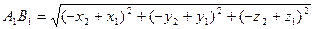
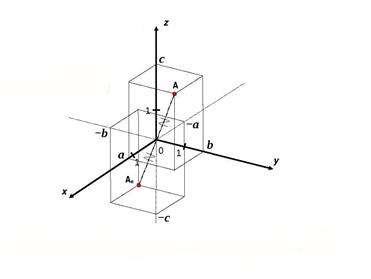
Рассмотрим теперь две точки А (x₁; y₁; z₁) и В (x₂; y₂; z₂) и докажем, что расстояние между симметричными им точкам А₁ и В₁ равно АВ. Точки А₁ и В₁ имеют координаты А₁ (-x₁; -y₁; -z₁ ) и В₁ (-x₂; -y₂; -z₂). По формуле расстояния между двумя точками находим: . Из этих соотношений ясно, что АВ=А₁В₁, что и требовалось доказать.

Построим точку А₀ симметричную точке А относительно точки О.

Пусть А (a; b; c). Тогда координаты A₀ (-a; -b; -c).

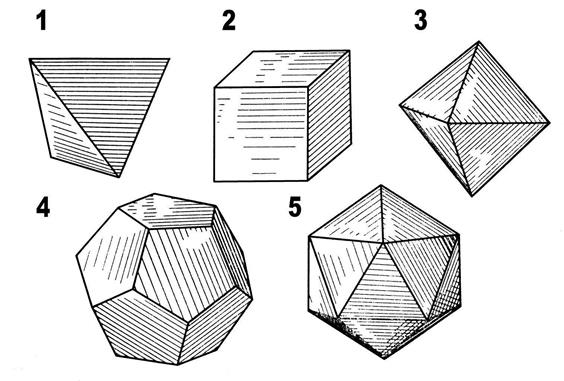
Фигуры, обладающие центральной симметрией.

1. – тетраэдр 2. – куб 3. – октаэдр 4. – додекаэдр 5. – икосаэдр

Применение центральной симметрии в жизни.

В архитектуре центральная симметрия используется реже осевой. Она присуща античным круглым храмам, используется в колоннах.

Колизей Пирамиды в Египте

Башни церквей, замков, колонны проектировались с учетом центральной симметрии. Такие сооружения предавали зданиям массивности. Башни одинаково роскошно выглядели с любой плоскости города.

Центральная симметрия в природе. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных.

Центральная симметрия прослеживается в

костюмах казанских татар

№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при центральной симметрии относительно начала координат.

При центральной симметрии относительно начала координат знаки координат искомых точек меняются на противоположные.

А (0; 1; 2) → А₁ (0; -1; -2)

В (3; -1; 4) → В₁ (-3; 1; -4)

С (1; 0; -2) → С₁ (-1; 0; 2)

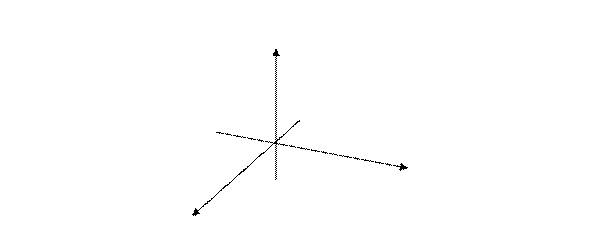
№ 2. Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя.

а)

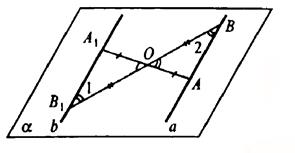
Через центр симметрии и данную прямую можно провести единственную плоскость. Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а. Пусть А ∈ а, построим отрезок ОА.

Продолжим ОА за точку О на расстояние ОА₁=АО. Получим точку А₁, симметричную А.

Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ₁=ОВ. Получим точку B₁, симметричную точке В.

Через А₁ и В₁ проведем прямую b. Рассмотрим ΔAОВ и ΔА₁ОВ₁⋅AО=А₁О, ВО=ОВ₁, ΔАОВ=ΔА₁ОВ₁ как вертикальные, следовательно, ΔAОВ=ΔА₁ОВ₁.

Тогда, ∠1=∠2 и а || b.

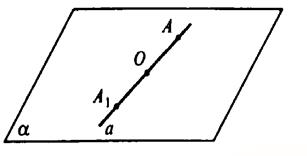
Пусть А ∈ а. Симметричная ей точка А₁ тоже принадлежит прямой а; АО=ОА₁.

Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.

Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно плоскости α.

Докажем, что зеркальная симметрия является движением.

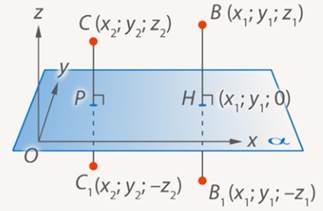
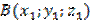
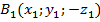
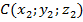
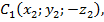
Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Oxy совпала с плоскостью симметрии, и установим связь между координатами точек и , и симметричных относительно плоскости Oxy

Найдем длину отрезков BC и B₁C₁ по формуле расстояния между точками:

Отсюда BC = B₁C₁, значит, зеркальная симметрия является движением.

Отсюда следует, что зеркальная симметрия обладает следующими свойствами:

· переводит прямые в прямые

· полупрямые – в полупрямые

· отрезки – в отрезки

· плоскости – в плоскости

· сохраняет углы между прямыми.

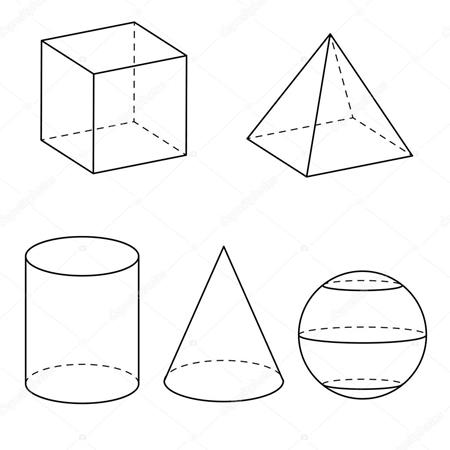
Фигуры, обладающие зеркальной симметрией

(слева на право) – куб, пирамида, цилиндр, конус, сфера

Зеркальная симметрия в жизни

Наиболее распространена вархитектуре зеркальная симметрия.

Эйфелева башня Тадж Махал

Зеркальная симметрия в природе может быть представлена отражением изображения в воде.

Животные, растения, и человек тоже могут послужить примерами зеркальной симметрии. Однако назвать их идеальными примерами сложно, ведь даже лицо человека, которое на первый взгляд может показаться симметричным, таковым не является.

№ 1. Найдите координаты точек, в которые переходят точки А (0; 1; 2), В (3; -1; 4), С (1; 0; -2) при зеркальной симметрии относительно координатных плоскостей.

Если плоскость симметрии — плоскость Оxy, то меняем значение координаты z на противоположную (т.к. ось Оz перпендикулярна плоскости Оxy, О – точка их пересечения)

А (0; 1; 2) → А₁ (0; 1; -2)

В (3; -1; 4) → B₁ (3; -1; -4)

С (1; 0; -2) → C₁ (1; 0; 2)

Аналогично решение с другими плоскостями.

Если плоскость симметрии — плоскость Оyz, то меняем значение координаты x.

А (0; 1; 2) → А₁ (0; 1; 2)

В (3; -1; 4) → B₁ (-3; -1; 4)

С (1; 0; -2) → C₁ (-1; 0; -2)

Если плоскость симметрии — плоскость Оxz, то меняем значение координаты y.

А (0; 1; 2) → А₁ (0; -1; 2)

В (3; -1; 4) → B₁ (3; 1; 4)

С (1; 0; -2) → C₁ (1; 0; -2)

№ 2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Докажите, что если: а) β || α, то β₁ || α; б) β ┴ α, то β₁ совпадает с β.

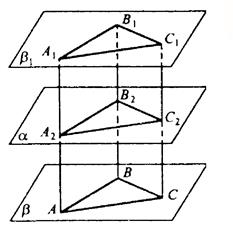
а) Выберем три точки в плоскости А, В, С, не лежащие на одной прямой. Проведем АА₂⊥α, ВВ₂ ⊥α, СС₂ ⊥α. Продолжим эти отрезки за точки А₁, B₁, C₁ так, что А₂А₁=АА₂, B₂B₁=BB₂, C₂C₁=CC₂.

Плоскость β₁ проходит через точки А₁, В₁ и C₁, она — единственная.

Если две пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум прямым (B₁A₁ и В₁С₁) другой плоскости (β₁), то эти плоскости параллельны: β₁ || β.

б)

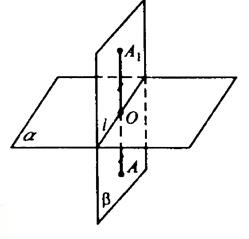
Пусть α⊥β. Возьмем произвольную точку А ∈ β и построим АО перпендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА₁=АО.

Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е.

АО⊂β, следовательно, и АА₁ ⊂β.

Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. тогда, плоскость β отображается сама на себя, или β₁ совпадает с β.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Материалы к уроку%: Центральная симметрия.

Видео:Центральная симметрия. 6 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Осевая и центральная симметрии. 6 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Центральная симметрия Точки А и А’ называются симметричными относительно точки О, если О является серединой отрезка АА’. Точка О считается симметричной сама себе. Преобразование плоскости, при котором каждой точке А сопоставляется симметричная ей относительно точки О точка А’, называется центральной симметрией. Точка О при этом называется центром симметрии.

Центральная симметрия Две фигуры F и F’ называются центрально-симметричными относительно центра О, если каждой точке одной фигуры соответствует симметричная точка другой фигуры. Фигура F называется центрально-симметричной относительно центра О, если она симметрична сама себе.

Свойства Свойство 1. Центральная симметрия сохраняет расстояния между точками. Свойство 2. Центральная симметрия переводит отрезки в отрезки, лучи в лучи и прямые в прямые. Свойство 3. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Вопрос 1 Какие точки называются симметричными относительно точки? Ответ: Точки А и А’ называются симметричными относительно точки О, если О является серединой отрезка АА’. Точка О считается симметричной сама себе.

Вопрос 2 Что называется центральной симметрией? Ответ: Центральной симметрией называется преобразование плоскости, при котором каждой точке А сопоставляется симметричная ей относительно точки О точка А’.

Вопрос 3 Какие фигуры называются центрально симметричными? Ответ: Две фигуры F и F’ называются центрально-симметричными относительно центра О, если каждой точке одной фигуры соответствует симметричная точка другой фигуры.

Вопрос 4 Какая фигура называется центрально симметричной? Ответ: Фигура F называется центрально-симметричной относительно центра О, если она симметрична сама себе.

Вопрос 5 Сформулируйте свойства центральной симметрии. Ответ: 1. Центральная симметрия сохраняет расстояния между точками. 2. Центральная симметрия переводит отрезки в отрезки, лучи в лучи и прямые в прямые. 3. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Вопрос 6 Какая точка при центральной симметрии переходит в себя? Ответ: Центр симметрии.

Вопрос 7 Какие прямые при центральной симметрии переходят в себя? Ответ: Прямые, проходящие через центр симметрии.

Упражнение 1 Имеет ли отрезок центр симметрии? Ответ: Да.

Упражнение 2 Ответ: В середине отрезка AA’. Центральная симметрия переводит точку А в точку А’. Где находится центр симметрии?

Упражнение 3 Имеет ли луч центр симметрии? Ответ: Нет.

Упражнение 4 Имеет ли центр симметрии пара пересекающихся прямых? Ответ: Да.

Упражнение 5 Имеет ли равносторонний треугольник центр симметрии? Ответ: Нет.

Упражнение 6 Имеет ли параллелограмм центр симметрии? Ответ: Да.

Упражнение 7 Верно ли утверждение о том, что если четырехугольник имеет центр симметрии, то он является параллелограммом? Ответ: Да.

Упражнение 8 Какие из фигур, изображенных на рисунке, имеют центр симметрии? Ответ: б), в), г), д).

Упражнение 9 На рисунке укажите буквы латинского алфавита, имеющие центр симметрии. Ответ: H, I, N, O, S, X, Z.

Упражнение 10 Всякий ли правильный многоугольник имеет центр симметрии?

Упражнение 11 Может ли фигура иметь более одного центра симметрии? Ответ: Да, например, прямая имеет бесконечно много центров симметрии.

Упражнение 12 Может ли центр симметрии фигуры не принадлежать ей? Ответ: Да, например, центр окружности является ее центром симметрии.

Упражнение 13 При каком расположении трех прямых образованная ими фигура имеет бесконечно много центров симметрии? Ответ: Две прямые параллельны третьей и находятся от нее на равных расстояниях.

Упражнение 14 Изобразите точку A’, симметричную точке A, относительно точки O.

Упражнение 15 Изобразите точку A’, симметричную точке A, относительно точки O.

Упражнение 16 Изобразите отрезок A’B’, симметричный отрезку AB, относительно точки O.

Упражнение 17 Изобразите отрезок A’B’, симметричный отрезку AB, относительно точки O.

Упражнение 18 Изобразите отрезок A’B’, симметричный отрезку AB, относительно точки O.

Упражнение 19 Изобразите прямую, симметричную данной прямой a относительно точки O.

Упражнение 20 Изобразите прямую, симметричную данной прямой a относительно точки O.

Упражнение 21 Изобразите треугольник A’B’С’, симметричный треугольнику ABC, относительно точки O.

Упражнение 22 Изобразите треугольник A’B’С’, симметричный треугольнику ABC, относительно точки O.

Упражнение 23 Изобразите треугольник A’B’С’, симметричный треугольнику ABC, относительно точки O.

Упражнение 24 Изобразите четырехугольник, симметричный четырехугольнику ABCD, относительно точки O.

Упражнение 25 Изобразите четырехугольник, симметричный четырехугольнику ABCD, относительно точки O.

Упражнение 26 Отрезки AB и CD являются центрально-симметричными. Укажите центр симметрии.

Упражнение 27 Треугольники ABC и DEF являются центрально-симметричными. Укажите центр симметрии.

Упражнение 27 Треугольники являются центрально-симметричными. Укажите центр симметрии.

Упражнение 27 Треугольники являются центрально-симметричными. Укажите центр симметрии.

Упражнение 28 Имеет ли четырехугольник, изображенный на рисунке, центр симметрии? Если да, укажите его.

Упражнение 29 Имеет ли четырехугольник, изображенный на рисунке, центр симметрии? Если да, укажите его.

Упражнение 30 Имеет ли шестиугольник, изображенный на клетчатой бумаге, клетками которой являются квадраты, центр симметрии?

Упражнение 31 Имеет ли восьмиугольник, изображенный на клетчатой бумаге, клетками которой являются квадраты, центр симметрии?

Упражнение 32 Изобразите треугольник, симметричный треугольнику OAB, относительно точки O.

Упражнение 33 Изобразите треугольник A’B’С’, симметричный треугольнику ABC, относительно точки O.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 688 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Материал ориентрован на урок по федеральным государственным образовательным стандартам. Предусмотрены все универсальные учебные действия. Показана межпредметная связь. Данный материал предназначен как для учителей, так и для учащихся при дополнительной работе с материалами учебников, при выполнении домашнего задания.

• Тележинская Елена ЛеонидовнаНаписать 1463 25.04.2018

Номер материала: ДБ-1508526

24.04.2018 572

22.04.2018 777

22.04.2018 167

22.04.2018 260

22.04.2018 190

22.04.2018 378

22.04.2018 290

22.04.2018 264

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

48. Осевая и центральная симметрииСкачать

Осевая и центральная симметрия, 6 классСкачать

Осевая симметрия. 6 класс.Скачать

Осевая и центральная симметрия.Скачать

СИММЕТРИЯ | осевая симметрия | центральная симметрияСкачать

Центральная и осевая симметрии. Геометрия 7 класс.Скачать

Осевая и центральная симметрияСкачать

Центральная симметрия. Как построить фигуру, симметричную данной относительно точкиСкачать

Центральная симметрияСкачать

Ось симметрииСкачать

МЕРЗЛЯК-6. ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. ПАРАГРАФ-44Скачать

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ: фигуры, обладающие центром симметрии, алгоритм построения симметричных фигурСкачать

Геометрия 11 класс (Урок№4 - Движения в пространстве.)Скачать

6 класс, 26 урок, СимметрияСкачать

Симметрия относительно прямойСкачать

Центральная симметрия | Задачи 21-25 | Решение задач | Волчкевич |Уроки геометрии в задачах 7-8Скачать