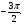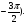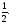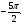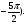Тригонометрия задания на окружность

Контрольный срез по теме «Тригонометрический круг» предназначен для проверки знаний учащихся 10 класса. В процессе выполнения заданий учащимся необходимо показать свои умения определять по кругу табличные значения тригонометрических функций, отмечать на тригонометрическом круге точки, соответствующие данным углам, а так же решать простейшие тригонометрические неравенства.

Просмотр содержимого документа
«Контрольный срез «Тригонометрический круг»»

Контрольный срез по материалу курса алгебры и начал анализа 10 класса

Отметьте на тригонометрическом круге точки, соответствующие углам:

а) б) в) г)

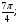
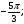
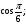
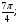
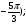
а) б) tg в) sin( г) cos(

Укажите множество точек окружности, для которых:

а) cost = б) sint =

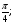
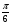
а) 2cos60 o – tg б) ctg45 o -2sin.

Укажите дугу окружности, множество точек которой удовлетворяет условию:

а) cost б) sint

Найдите наименьшее и наибольшее значение выражения 0,5cost +2.

Контрольный срез по материалу курса алгебры и начал анализа 10 класса

Отметьте на тригонометрическом круге точки, соответствующие углам:

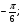
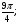
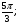
а) б) в) г)

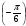
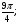
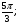
а) cos; б) tg в) sin г) cos(

Укажите множество точек окружности, для которых:

а) cost = 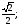б) sin t =

Укажите дугу окружности, множество точек которой удовлетворяет условию:

а) cos t б) sin t

Найдите наименьшее и наибольшее значение выражения 3sin t – 1 .

Оценка «3» , если набрано 10 – 12 баллов; Оценка «4» , если набрано 13 – 15 баллов;

Оценка «5» , если набрано 16 — 20 баллов.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Рабочая тетрадь по тригонометрии «Работа с единичной окружностью»

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ГБПОУ «Челябинский государственный колледж индустрии питания и торговли»

раздел «Основы тригонометрии»

«Работа с единичной окружностью»

Студента группы № _____________

РАССМОТРЕНА И СОГЛАСОВАНА:

На заседании ЦМК

Протокол № __от _______2021г.

Председатель_______/ Э.С. Нуруллина /

Рабочая тетрадь по математике предназначена для изучения раздела «Основы тригонометрии».

Составитель: А.Я. Амелина, преподаватель математики первой квалификационной категории.

Содержательная и техническая экспертиза проведена ____________________________________

Тема: Тригонометрические уравнения

Задание 11. На листе миллиметровой бумаги построить единичную окружность и касательные к ней в точках (1;0) и (0;1), выбрав за единицу масштаба 5 см. Решить приближенно уравнения.

1 Вариант: tgx =0,7; ctgx =-1,4.

2 Вариант: tgx = -0,5; ctgx =0,9

Ответ:

Тема: Тригонометрические уравнения

Задание 10. С помощью единичной окружности, построенной на миллиметровой бумаге, и транспортира приближенно решить уравнения, ответ записать в радианной мере. За единицу масштаба выбрать 5см. Уточнить ответ с помощью калькулятора.

1 Вариант : sinx=0.32 ; cosx=0.66

2 Вариант : sinx=0.74 ; cosx=0.26

Рекомендации к выполнению: Учитываем, что sinx — это ордината точки числовой окружности, а cosx — абсцисса. Значит, необходимо найти на числовой окружности точки с соответствующими ординатами (абсциссами), учитывая масштаб в котором построена единичная окружность (Напр. 0.32=50мм·0.32=16мм) и с помощью транспортира померить углы, которым они соответствуют. Затем перейти от градусов к радианам по формуле: n °=π· n /180 рад.

Рабочая тетрадь является учебным пособием к сопровождению уроков по учебной дисциплине «Математика» раздела «Основы тригонометрии».

Разработана в соответствии с учебной программой и содержит необходимые рекомендации о порядке выполнения упражнений.

В процессе работы с числовой окружностью у учащихся должны быть сформированы следующие умения:

— находить на числовой окружности точки, соответствующие заданным числам;

— составлять аналитические записи для дуг числовой окружности;

— определять принадлежность точки какой-либо координатной четверти;

— находить координаты точек числовой окружности и отыскивать на числовой окружности точки по заданным координатам;

— определять синус, косинус, тангенс угла;

— решать с помощью единичной окружности простейшие тригонометрические уравнения и неравенства.

Использование готовых дидактических материалов позволяет экономно расходовать время на уроке, а также способствовать более глубокому освоению знаний раздела «Основы тригонометрии».

Тригонометрическая окружность — окружность единичного радиуса с центром в начале координат (рис.1).

За нулевое положение радиуса, принимается его положение на положительном направлении оси Ox. Угол поворота радиуса отсчитывается от положительного направления оси Ox: с плюсом – против часовой стрелки, с минусом – по часовой стрелке. Полный круг – это 360°. Каждому углу α от 0° до 360° соответствует точка М на единичной окружности.

Углы обычно измеряются либо в градусах, либо в радианах. Перевести градусы в радианы просто: 360 градусов (полный круг) соответствует 2π радиан .

На единичной окружности также можно

находить углы, которые больше 360 градусов.

Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые

Тема: Тригонометрические операции

Задание 9. На листе миллиметровой бумаги построить первую четверть единичной окружности, выбрав за единицу масштаба 10см. Провести ось тангенсов (параллельна оси синусов и проходит через точку (1;0)). Составить таблицу тангенсов углов от 0° до 60° с шагом в 10°. Перевести значения углов в радианную меру. Результаты занести в таблицу. Сравнить полученные значения с табличными, оценить относительную ошибку измерений.

Рекомендации к выполнению: С помощью транспортира отмеряем углы в 0°, 10°, 20° и т.д. Соединяем эти точки с началом координат – точкой (0;0) лучом и смотрим, где этот луч пересекает ось тангенсов. Учитывая масштаб : 1единица-100мм, расчитываем значения тангенса по формуле: tgx =Хмм/100мм. Результаты заносим в таблицу.

Тема: Тригонометрические операции

Задание 8. На миллиметровой бумаге построить единичную окружность, приняв за единицу 5 см, а затем центральный угол α, такой что:

1 вариант: sinα =-0,5; tgα =2.

2 вариант: cosα =0,3; tgα =-1,5.

Рекомендации к выполнению: При выполнении этого задания необходимо знать, что значения sinx — располагаются на оси х, значения cosx — на оси у, а значения tgx — на прямой параллельной оси у, проходящая через точку с координатами (1;0). Учитывая масштаб, в котором построена единичная окружность, находим соответствующие точки на осях. Через эти точки проводим прямые: для синуса — параллельно оси х, для косинуса – параллельно оси у, для тангенса – соединяем полученную точку на прямой тангенса с началом координат. С помощью транспортира измеряем углы, которым они соответствуют.

Тема: Углы и вращательное движение

Задание 1. Отметить на единичной окружности точки, соответствующие данным числам (углам поворота):

1 Вариант :

2 Вариант :

Рекомендации к выполнению: Для отыскания точек, соответствующих положительным числам нужно пройти по окружности путь заданной длинны, двигаясь из точки А против часовой стрелки, для отрицательных чисел – по часовой стрелке. При этом учитываем, что длинна каждой четверти единичной окружности равна π/2.

Тема: Углы и вращательное движение

Задание 2. Отметить на единичной окружности примерное положение точек, соответствующих числам:

1 Вариант : 1, — 2, 3, — 4, 5, — 6

2 Вариант : -1, 2, -3, 4 , -5, 6

Образец решения задачи: Дана точка -7. Необходимо из точки А двигаться в отрицательном направлении (по часовой стрелке), пройти по окружности путь длинной 7. Если мы пройдем одну окружность, то получим (приближенно) 6,28, значит нужно пройти ещё (в том же направлении) путь длинной 0,72. Это дуга, немного меньше половины четверти окружности, т.е. её длинна меньше числа π/4, т.к. π/4≈0,785 т.е. мы немного не дойдем до середины четвертой четверти.

Тема: Тригонометрические операции

Задание 7. Построить на миллиметровой бумаге единичную окружность, приняв за единицу 5 см. С помощью этой окружности и транспортира найти синусы и косинусы данных ниже углов с возможно большей точностью. Проверить полученные результаты по калькулятору (При аккуратных построениях ошибка не должна превышать 0,04).

1 вариант: .

2 вариант: .

Рекомендации к выполнению: См. образец решения задания №3 и рекомендации к выполнению задания №6.

Тема: Тригонометрические операции

Задание 6. Построить на миллиметровой бумаге единичную окружность, приняв за единицу 5см. С помощью этой окружности и транспортира найти синусы и косинусы данных ниже углов с возможно большей точностью.

; ; ; .

Результаты занести в таблицу:

Рекомендации к выполнению: Переходим от радиан к градусам используя равенство: π=180°. С помощью транспортира отмеряем соответствующий угол и обозначаем точку на единичной окружности. Из полученной точки опускаем перпендикуляр на ось х (значения cosx ) и ось y (значения sinx ). Считаем в мм значения sinx и cosx , переходим к единицам по формуле: .

Тема: Углы и вращательное движение

Задание 3. Отметить на единичной окружности точки соответствующие каждому из чисел заданного множества:

1.

2.

3.

4.

5.

6.

Образец решения задачи : Задано множество чисел –π/3+2πk, k є Z . Любые два числа из этого множества чисел отличаются на величину кратную 2π. Значит, результаты поворотов на эти углы совпадают, т. е. всем числам соответствует одна и та же точка. Достаточно найти точку, соответствующую одному из чисел; при k=0 имеем –π/3.

Тема: Углы и вращательное движение

Задание 4. Отметить на единичной окружности точки, соответствующие числам заданного множества:

1.

2.

3.

4.

5.

6.

Тема: Тригонометрические операции

Задание 5 . С помощью единичной окружности составить таблицу синусов и косинусов следующих углов (чисел):

0; ; ; ; ; ; ; ; .

Результаты занести в таблицу:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Видео:Тригонометрическая окружность. Как выучить?Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 930 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 335 человек из 72 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Краткое описание документа:

Рабочая тетрадь по тригонометрии предназначена для работы со студентами 1 курса колледжа или техникума, также может использоваться на уроках алгебры в 10 классе.

Общая информация

Похожие материалы

» Входное тестирование » 9 класс

Урок алгебры на тему «Теорема Виета» (8 класс)

Входная контрольная работа в форме ВПР (8 класс)

Итоговая контрольная работа по учебной дисциплине «Математика»

Интегрированный урок (информатика – математика).

Итоговая контрольная работа по учебной дисциплине «Математика» (1 курс)

Математический квест для учащихся 7-х классов

Входная контрольная работа по математике для 11 класса.

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5459401 материал.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

Утвержден список федеральных инновационных площадок в образовании на 2022 год

Время чтения: 1 минута

В Госдуме обсудят введение обязательных тестов на наркотики в школах

Время чтения: 1 минута

Онлайн-конференция об управлении общеобразовательной организацией

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:12 часов Тригонометрии с 0.Скачать

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:Тригонометрическая окружность. Задание 13 | Математика ЕГЭ | УмскулСкачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:Тригонометрия. 10 класс. Вебинар | МатематикаСкачать

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Видео:Отбор корней по окружностиСкачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Формулы приведения с нуля за 15 минут!Скачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Формулы приведения - как их легко выучить!Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

📺 Видео

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Как искать точки на тригонометрической окружности.Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Тригонометрия с нуля. Как решать любые задачи через окружность. ЕГЭ 2024Скачать

Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать