Треугольник вписан в окружность угол а 60

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Построить угол 60°Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Треугольник ABC вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

В прямоугольном треугольнике ABC ZC = 90°, A = 60°. В этот треугольник вписана окружность, которая касается сторон АВ, ВС и АС соответственно

Видео:Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Ваш ответ

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

решение вопроса

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,949
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов?

Геометрия | 10 — 11 классы

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов.

Найдите величину дуги АВ, если дуга АВ равна двум дугам ВС.

Обозначит дугу АВ за 2х, а ВС за х

К. угол В вписанный дуга АС = 120

2х + х + 120 = 360

дуга АВ = 80 * 2 = 160.

Видео:Геометрия В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касаетсяСкачать

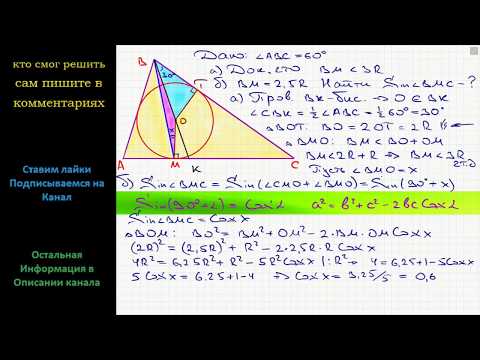
ПОМОГИИИТЕЕ?

В окружность вписан треугольник АВС так, что сторона АС является диаметром этой окружности.

Найдите углы треугольника АВС, если дуга ВС = 108 градусов.

Видео:В треугольнике ABC углы A и C равны 20° и 60° ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

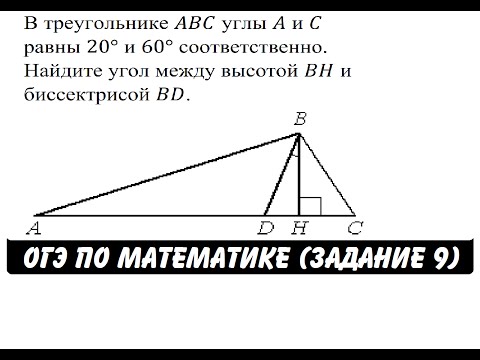
Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Угол АКВ вписан в окружность и равен 45 градусов?

Угол АКВ вписан в окружность и равен 45 градусов.

Найдите дугу АВ, если R = 4.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно?

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно.

Найдите дугу MK, дугу MN, дугу NK, если угол АВС = 62 градусам, угол АСВ = 68 градусам.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Точки А, В, С лежат на окружности с центром О?

Точки А, В, С лежат на окружности с центром О.

Угол АОВ = 80 градусов, дуга АС : на дугу ВС — 2 : 3.

Найдите углы треугольника АВС.

Видео:№223. Найдите угол С треугольника ABC, если: a) ∠A=65°, ∠B = 57°; б) ∠A = 24°, ∠B= 130Скачать

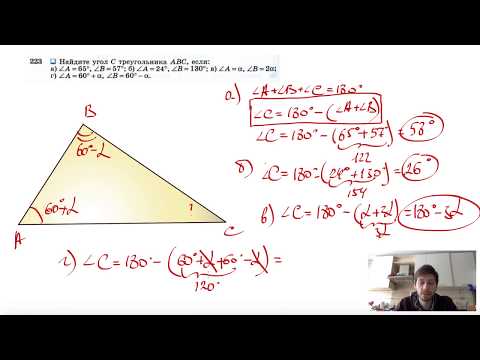
В окружность вписан треугольник АВС так, что АВ — диаметр окружности?

В окружность вписан треугольник АВС так, что АВ — диаметр окружности.

Найдите углы треугольника, если дуга АС = 70 градусов (Помогите пжл : * ).

Видео:№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

Треугольник АВС, у которого АС = 6, угол А = 75 градусов , угол В = 30 градусов, вписан в окружность?

Треугольник АВС, у которого АС = 6, угол А = 75 градусов , угол В = 30 градусов, вписан в окружность.

Найдите длины дуг окружности, концами которых являются вершины треугольника.

Видео:Треугольник, вписанный в окружность геометрия 7 классСкачать

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС?

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС.

Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

В окружность вписан треугольник АВС так, что АВ – диаметр окружности?

В окружность вписан треугольник АВС так, что АВ – диаметр окружности.

Найдите углы треугольника, если дуга ВС = 134°.

Вы открыли страницу вопроса Треугольник АВС вписан в окружность, угол АВС равен 60 градусов?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Пусть О — точка пересечения диагоналей прямоугольника. Расстоянием от точки О до стороны АВ будет перпендикуляр ОН, опущенный из точки О к АВ. ОН⊥АВ, ВС⊥АВ, значит ОН║ВС. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Значит..

Пусть 1 угол х тогда 2 угол х + 24 × + × + 24 = 180 2× = 156 × = 78 — 1 угол 2 — 78 + 24 = 102.

Для удобства решения , перенесём симметрично точку K в нижнее основание ABCD (все пересечения абсолютно те же) то есть точкам A, B, C, D соответствуют точки A1, B1, C1, D1. Тогда точка K пересечения прямых BM и AN . Найдём соотношение BK / KM , про..

3 — 1, а 5 — 2. Точно не знаю.

3) 1, решение : 180 — 65 = 115 115 = 75 + 40 5) 1, решение : ОКВ = 90 градусов, значит OKV = 45 градусов, углы VOK = VKO, значит треугольник vko равнобедренный, то есть VO = VK, отсюда BO = OV умножить на 2, что равно 7 * 2 = 14 вроде так, , , , , , ..

Так оно же разное может быть.

Любая сторона треугольника меньше суммы двух других сторон и больше их разности. 7 + 13 = 20 — длина третьей стороны не может превышать 19 см. 13 — 7 = 6 — длина третьей стороны не может быть меньше 7 см. Все простые числа от 7 до 19 : 7, 11, 13, ..

|КР| = ✓((3 — ( — 3))² + ( — 4 — 2)²) = ✓(36 + 36) = ✓72 = 6✓2 Пусть М — середина отрезка. Её координаты равны полусумме соответствующих координат точек К и Р М(( — 3 + 3) / 2 ; (2 + ( — 4)) / 2) М(0 ; — 1).

Смежные углы = 180 ° = >.

Биссектрисы углов отсекают от прямоугольника равнобедркнные треугольники (свойство биссектрис). В случае, когда биссектрисы пересекаются на стороне ВС, имеем : АВ = ВМ и CD = МС. Значит сторона ВС = АВ + CD или 2 * АВ. Полупериметр равен 42 : 2 = ..

🌟 Видео

Геометрия, 10 класс | Треугольники с углами 60 и 120 градусов. Часть 1Скачать