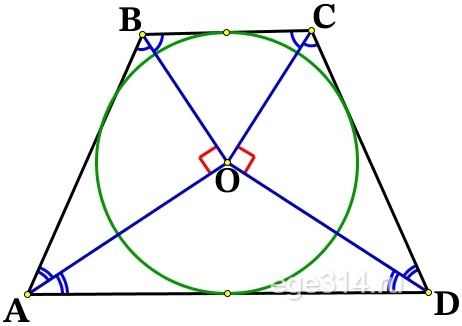
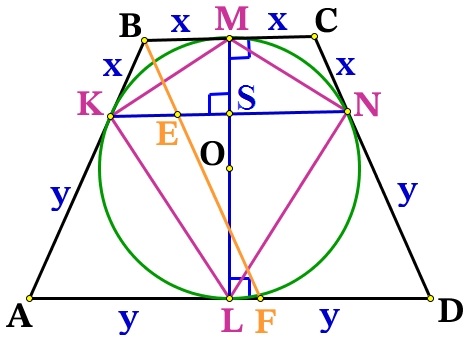
Трапеция abcd описана около окружности ab cd точки касания (5 видео)

Решение №2566 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac площади трапеции ABCD.

Источник: Ященко ЕГЭ 2022 (36 вар)

а)

Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.

∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°

Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:

Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:

∠AOB = ∠COD = 90°

Что и требовалось доказать.

б) Найти: frac , если АВ = СD, S_=fraccdot S_ :

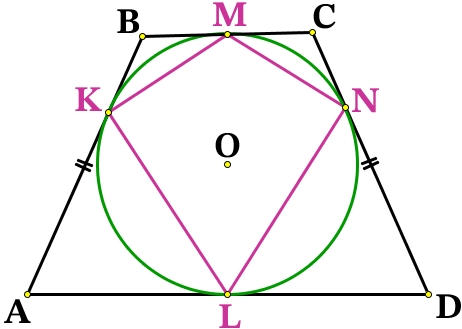
Отрезки касательных к окружности, проведённые из одной точки, равны:

BM = BK
CM = CN
AK = AL
DL = DN

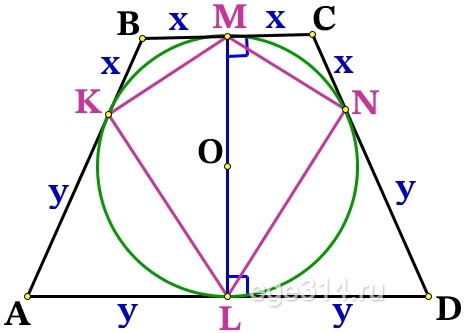
Т.к. AB = CD, то:

BK = СN = BM = CM = x
AK = DN = AL = DL = y

Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:

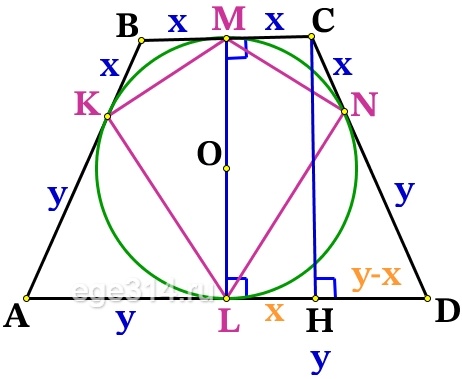
Проведём ещё одну высоту трапеции СН:

MC = LH, МCHL – прямоугольник, значит MC = LH = x , найдём HD:

HD = LD – LH = y – x

Из прямоугольного ΔСHD по теореме Пифагора найдём СН:

СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=sqrt=2sqrt

Выразим площадь S_{ABCD :}

В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.

ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:

Найдём диагональ KN:

Выразим площадь S_KMNL :

S_=fraccdot MLcdot KNcdot sin angle MSK=fraccdot 2sqrtcdot fraccdot sin 90^=sqrtcdot fraccdot 1= frac<4xysqrt>

Подставим выраженные площади с исходное отношение:

Т.к. у нас у большее основание, а х меньшее, то их отношение равно 6.

Содержание

Около окружности описана равнобочная трапеция ABCD с основаниями AD и ВС, М и К — точки касания окружности с А В и CD, Р — точка касания с AD. В каком отношении отрезок МК делится отрезком ВР
Ваш ответ
Похожие вопросы
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС
🎦 Видео

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Около окружности описана равнобочная трапеция ABCD с основаниями AD и ВС, М и К — точки касания окружности с А В и CD, Р — точка касания с AD. В каком отношении отрезок МК делится отрезком ВР

Видео:В трапеции ABCD AB=CD, ∠BDA=35° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:Задача про трапецию, описанную около окружностиСкачать

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС

Задача. Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что ∠AOB = ∠COD = 90°.

б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со всеми сторонами трапеции составляет 12/49 площади трапеции ABCD.

а) По условию трапеция ABCD с основаниями AD и ВС описана около окружности с центром О, следовательно, точка О есть пересечение биссектрис всех углов трапеции. Так как сумма углов трапеции, прилегающих к боковой стороне АВ, равна 180°, то сумма половинок этих углов равна 90°. Таким образом в ΔАОВ

∠OАB + ∠АВО = 90°, значит, и ∠АОВ = 90°.

Аналогично, так как ∠BCD + ∠ADC = 180°, то в ΔСOD

∠OCD + ∠ODC = 90°, следовательно, и ∠COD = 90°. Доказано.

б) По условию равнобедренная трапеция ABCD с основаниями AD и ВС описана около окружности с центром О. Пусть эта окружность касается сторон трапеции в точках М, Р, N и К. Четырёхугольник MPNK является вписанным в данную окружность. Радиус, проведённый в точку касания перпендикулярен касательной.

РК – диаметр окружности, перпендикулярен к основаниям трапеции и проходит через их середины, так как длины касательных, проведённых из одной точки к окружности, равны. РК – ось симметрии данной трапеции и четырёхугольника МРNК. Будем рассматривать половину данной трапеции слева от РК.

Площадь Δ МРК состоит из суммы площадей двух равновеликих треугольников МОР и МОК.

Действительно, площадь каждого из них равна половине произведения двух сторон (радиусов окружности) на синус угла (с вершиной в точке О) между ними; значения синусов смежных углов равны.

Проведём ОВ. Это биссектриса угла В трапеции ABCD.

В равнобедренном треугольнике МВР биссектриса ВТ является и медианой, и высотой (Т – середина МР, ВТ⟘МР). Тогда медиана ОТ (высота и биссектриса) делит равнобедренный треугольник ОМР на два равных треугольника РТО и МТО.

Аналогично рассуждая относительно ОА – биссектрисы угла А трапеции ABCD, делаем вывод, что равны треугольники МЕО и КЕО. Половинки равновеликих треугольников МОР и МОК также равновелики (и равны), значит, треугольник МРК состоит из четырёх равных треугольников, поэтому, разделив его площадь на 4, получим:

Выделим эти треугольники жёлтым цветом.

Итак, в рассматриваемой прямоугольной трапеции АВРК остаются:

Δ ВТР = Δ ВТМ (закрасим зелёным цветом) и

Δ АЕК = Δ АЕМ (закрасим розовым цветом).

Сумма этих четырёх, попарно равных треугольников, равна

Делим это значение пополам. Получаем:

В задаче требуется найти отношение AD : BC.

Обозначим AD = a, BC = b.

Нам нужно найти значение a : b.

По свойству касательных, проведённых из одной точки к окружности:

ОМ –радиус окружности, проведённый в точку касания, является высотой в прямоугольном треугольнике АОВ. По свойству пропорциональных отрезков в прямоугольном треугольнике

РТ – высота прямоугольного треугольника ВРО, проведённая к гипотенузе ВО, делит треугольник ВРО на подобные треугольники ВТР и РТО с коэффициентом подобия, равным отношению сходственных сторон:

Отношение площадей подобных треугольников равно квадрату их коэффициента подобия.

Точно так же, КЕ – высота прямоугольного Δ АКО, проведённая к гипотенузе АО, делит этот треугольник на подобные треугольники АЕК и КЕО. Тогда коэффициент их подобия: