Точка q лежит внутри треугольника mnk от этой точки отложены векторы

Видео:№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

Ваш ответ

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

решение вопроса

Видео:№787. Точка О — середина медианы EG треугольника DEF. Выразите вектор DO черезСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:81. Откладывание вектора от данной точкиСкачать

Банк задач для поэлементного контроля знаний по теме «Векторы» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Банк задач для поэлементного контроля знаний по теме «Векторы»

В четырехугольнике АВС D О – точка пересечения диагоналей. Прямая m проходит через точку О и пересекает стороны ВС и А D в точках М и N соответственно. Среди векторов найдите:

а) коллинеарные векторы;

б) сонаправленные векторы;

в) противоположные векторы;

г) равные векторы;

д) векторы, имеющие равные длины.

Р B F PKEF – параллелограмм. А и В – середины КЕ и PF соответственно. Запишите:

а) все векторы, изображенные на рисунке;

г) Равны ли векторы и ?

Д) Равны ли векторы по абсолютной величине?

3. Задача на построение. а) постройте ненулевой вектор с началом в точке О, коллинеарный вектору ; б) сонаправленный с вектором ; в) противоположно направленный вектору г) отложите от точки О вектор, равный вектору .

4. Стороны прямоугольника ABCD равны 3 дм и 4 дм. Найдите длину вектора .

5. В ромбе АВС D . От вершин А и В отложены векторы равные соответственно. Найдите длину вектора .

6. Точка М лежит внутри треугольника АВС. От этой точки отложены векторы равные векторам соответственно. Докажите, что — параллелограмм.

7 . Диаметр АС и хорда АВ образуют угол в 30. А радиус окружности равен 7 см. Внутри данной окружности выбрана точка К и от нее отложены векторы , равные соответственно. Найдите длину вектора .

8. Используя правило треугольника, найдите сумму векторов:

9. Используя правило треугольника, постройте и Определите вид четырехугольника ОАВС.

10. Докажите, что если при параллельном переносе, переводящем точку А в точку В, точка С переходит в точку K , то векторы равны.

11. Даны параллелограмм АВС D и точка О. Докажите, что

12. Даны произвольные точки А, В, С, D , E . Докажите, что =

13. Среди данных сумм найдите равные: ;.

14. В С В трапеции АВС D , AD BC .

см, АВ = 3 см. Найдите ||.

15. В трапеции ВСЕН, ВН = 2СЕ, точка о – середина ВН. Какие векторы с концом и началом в отмеченных точках являются противоположными вектору .

16. В трапеции АВС D , AD ǁ BC , ͦ , AD = 6м, АВ = 3 м.

17. В равнобедренном треугольнике АВС точка — середина основания АС.

а) Упростите выражение ;

б) Найдите ||, если АВ = 10см, .

18. В параллелограмме АВС D О – точка пересечения диагоналей.

а) Упростите выражение ;

б) Найдите ||, если АВ = 10 см, ВС = 12 см, а перпендикуляр, опущенный из вершины В на диагональ ВС равен 8 см.

19 . Начертите неколлинеарные векторы Постройте векторы

20. В равнобедренной трапеции АВС D меньшее основание равно боковой стороне, большее основание А D равно 20см, Найдите ||.

21. Отрезок АМ – медиана треугольника АВС. Выразите векторы через векторы

22. Начертите вектор и вектор так, что:

23 . Отложите от точки О векторы , , .

24. В С АВС D – трапеция. , ,

О . Выразить через и

25. В параллелограмме ABCE на стороне ВС взята точка Р так, что

ВР: РС = 3: 1, О – точка пересечения диагоналей. Выразите векторы и через векторы и .

26 . В параллелограмме ABCD на стороне АВ и диагонали АС взяты точки Е и К соответственно так, что АЕ : ЕВ = 3 : 2, АК : КС = 5 : 2. Выразите векторы через векторы и

27. В трапеции ABCD AB ǁ CD , AB = 3 CD . Выразите через векторы и векторы и где М – середина ВС, а N – точка на стороне АВ, такая, что AN : ND = 2 : 3.

28. Даны четырехугольник ABCD произвольная точка О. Известно, что , Найдите остальные углы этого четырехугольника.

29. На сторонах АВ и ВС треугольника АВС отмечены соответственно точки М и Н так, что АМ = 4ВМ, СН = 4ВН. Докажите, что МН ǁ АС и МН : АС = 1,5.

30. На окружности с центром О постройте такие точки а, в, с, что:

Итоговая тематическая контрольная работа по теме «Векторы».

Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б)

Дан параллелограмм АВС D . Найдите сумму векторов: а) и ; б) и ; в) и .

На стороне ВС ромба АВС D лежит точка К так, что ВК = КС. О – точка пересечения диагоналей. Выразите векторы , через векторы и .

В трапеции АВС D ВС : AD = 1 : 2, Е – середина боковой стороны СВ, точка М лежит на АЕ так, что АМ : МЕ = 4 : 1. Используя векторы, докажите, что точка М лежит на диагонали В D .

В равнобедренной трапеции один из углов равен , боковая сторона равна 8см, а меньшее основание 7см. Найдите среднюю линию трапеции.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

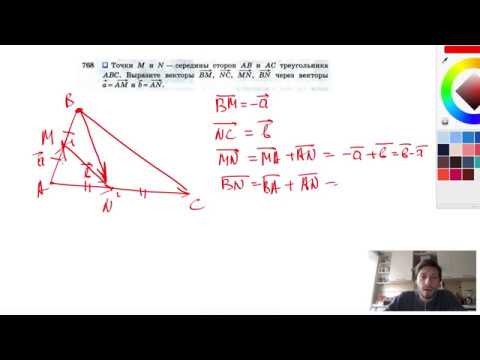
Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 510 469 материалов в базе

Другие материалы

• 08.11.2016
• 883
• 0

• 08.11.2016
• 355
• 0

• 08.11.2016
• 380
• 0

• 08.11.2016
• 348
• 0

• 08.11.2016
• 665
• 1

• 08.11.2016
• 447
• 1

• 08.11.2016
• 993
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.11.2016 1959
• DOCX 169.6 кбайт
• 14 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Козуб Эльвира Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 14774
• Всего материалов: 15

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

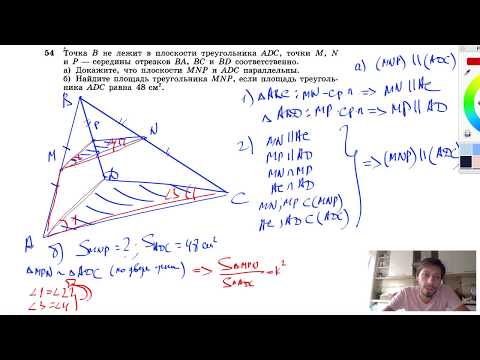
Видео:№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В Тюменской области школы и колледжи перевели на дистанционное обучение

Время чтения: 1 минута

В Новосибирской области школьников переведут на удаленку

Время чтения: 1 минута

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Как определить лежит ли точка внутри треугольника или снаружи.

Калькулятор поможет определить находится ли заданная точка внутри заданного треугольника. Точка и треугольник задаются декартовыми координатами на плоскости. Детально описан алгоритм вычисления.

Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором.

Точка в треугольнике

Векторное произведение ( z — координата )

Видео:№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать

Точка внутри треугольника. Описание алгоритма.

Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так:
[1].
Векторное произведение обладает свойством антикоммутативности:

Это важное свойство мы будем использовать для решения нашей задачи.

Попарное векторное произведение векторов-сторон треугольника и вектора из вершины в точку

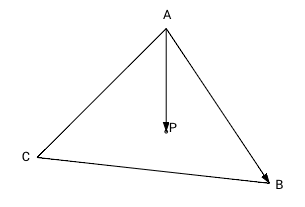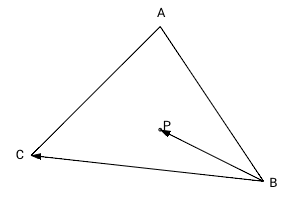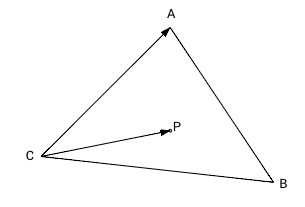
Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю — координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго — отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю.
Получив результаты по трем векторным произведениям, нам остается их проанализировать, чтобы понять лежит ли точка внутри треугольника:
Если мы имеем и положительные и отрицательные результаты, точка лежит вне треугольника, если результаты только положительные или только отрицательные, точка — внутри.
Таблица далее иллюстрирует все возможные варианты результатов векторного произведения:

🎥 Видео

Геометрия 9 Откладывание вектора от данной точкиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

8 класс, 42 урок, Откладывание вектора от данной точкиСкачать

Координаты точки и координаты вектора 1.Скачать

Откладывание вектора от данной точки | Геометрия 7-9 класс #78 | ИнфоурокСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

№34. Точка D не лежит в плоскости треугольника ABC, точки М, N и Р — середины отрезков DA, DBСкачать