Точка м лежит вне плоскости проходящей через точки а б и с может ли четырехугольник

Вопрос по геометрии:

Точка М лежит вне плоскости, проходящей через точки А, В и С. Может ли четырехугольник АВСМ быть трапецией? Ответ обоснуйте.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Если точки A,B,C лежат на одной прямой, то ABCM, очевидно, не является трапецией.

Пусть точки A,B,C не лежат на одной прямой. Тогда существует единственная плоскость (ABC), которая содержит все три эти точки. Так как точка M не лежит в (ABC), то не существует плоскости, в которой лежат все 4 точки A,B,C,M. Значит, четырехугольник ABCM является пространственным (не лежит ни в какой плоскости).

Из планиметрии известно, что трапеция — плоская фигура, поэтому четырехугольник ABCM трапецией быть не может.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№22. Точки А и В лежат в плоскости а, а точка С не лежит в этой плоскости.Скачать

Точка М лежит вне плоскости, проходящей через точки А, В и С?

Геометрия | 10 — 11 классы

Точка М лежит вне плоскости, проходящей через точки А, В и С.

Может ли четырехугольник АВСМ быть трапецией?

Если точки A, B, C лежат на одной прямой, то ABCM, очевидно, не является трапецией.

Пусть точки A, B, C не лежат на одной прямой.

Тогда существует единственная плоскость (ABC), которая содержит все три эти точки.

Так как точка M не лежит в (ABC), то не существует плоскости, в которой лежат все 4 точки A, B, C, M.

Значит, четырехугольник ABCM является пространственным (не лежит ни в какой плоскости).

Из планиметрии известно, что трапеция — плоская фигура, поэтому четырехугольник ABCM трапецией быть не может.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Точки А, В, С, D не лежат в одной плоскости?

Точки А, В, С, D не лежат в одной плоскости.

Пересекаются ли плоскости, проходящие через точки В, D, C и A, C, D?

Видео:№12. Точки А, В, С, D не лежат в одной плоскости. Пересекаются ли плоскости, проходящие через точкиСкачать

Прямая а, которая лежит в плоскости треугольника АВС, пересекает сторону АС в точке К?

Прямая а, которая лежит в плоскости треугольника АВС, пересекает сторону АС в точке К.

Может прямая а пересекать сторону ВС?

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Точка М лежит на ребре ВС параллелепипеда ABCDA1B1C1D1?

Точка М лежит на ребре ВС параллелепипеда ABCDA1B1C1D1.

Постройте сечение параллелепипеда плоскостью, проходящей через точку М и параллельной плоскости B1C 1D.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

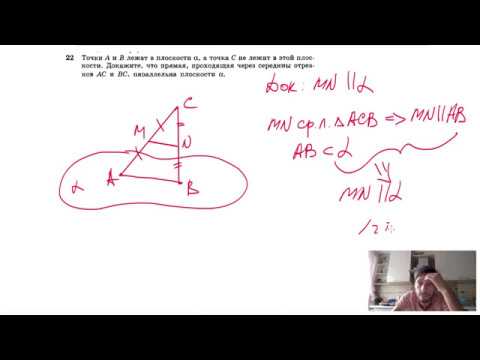
Точки А и В лежат на плоскости альфа, а точка О — вне плоскости?

Точки А и В лежат на плоскости альфа, а точка О — вне плоскости.

Докажите, что прямая , проходящая через середины отрезков ОА и ОВ, параллельна плоскости альфа.

С рисунком и решением.

Видео:№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

Точка р не лежит в плоскости трапеции авсд с основаниями ад и вс?

Точка р не лежит в плоскости трапеции авсд с основаниями ад и вс.

Докажите что прямая проходящая через середины рв и рс параллельна средней линии трапеции.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Привет, есть две задачи — решение дайте в виде рисунка ?

Привет, есть две задачи — решение дайте в виде рисунка .

1. Дана прямая а и точка А на ней.

Провести плоскость проходящая через точку А перпендикулярна прямой а.

2. Дана плоскость альфа и точка А вне её .

Провести через точку А прямую которая была бы перпендикулярна плоскости альфа.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Помогите пожалуйста?

Точкм А лежит в плоскости (а), точка В вне этой плоскости.

Через точки А и В провести прямую.

Начертить расстояние от точки В до плоскости (а) и расстояние от точки С (середина отрезка АВ) до плоскости (а).

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Точка m не лежит в плоскости треугольника abc?

Точка m не лежит в плоскости треугольника abc.

Каково взаимное расположение прямых ma и bc?

Видео:10 класс, 2 урок, Аксиомы стереометрииСкачать

Постройте сечение прямой четырехугольной призмы ABCDA1B1C1D1 плоскостью, проходящей через точки A, B и точку K, которая лежит на ребре DD1?

Постройте сечение прямой четырехугольной призмы ABCDA1B1C1D1 плоскостью, проходящей через точки A, B и точку K, которая лежит на ребре DD1.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Точки A и B лежат в плоскости альфа, а точка С не лежит в этой плоскости?

Точки A и B лежат в плоскости альфа, а точка С не лежит в этой плоскости.

Докажите, что прямая, проходящая через середины отрезков АС и ВС, параллельна плоскости альфа.

Вы находитесь на странице вопроса Точка М лежит вне плоскости, проходящей через точки А, В и С? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

DAC = (70 градусов — 20 градусов) : 2 = 25 градусов.

Ответ 2, 3. В треугольнике против большего угла лежит БОЛЬШАЯ сторона.

∠NSK + ∠KSM = 180 ∠NSK — ∠KSM = 40 складываем уравнения, получаем : 2∠NSK = 220 ∠NSK = 110° ∠KSM = 180 — 110 = 70° биссектриса ∠NSK делит его на два угла по 55° биссектриса ∠KSM делит его на два угла по 35° угол между биссектрисами = 55 + 35 = 90°.

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны. Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности. В нашем случае a + c =..

Лучше в YouTube посмотри, там подробно расскажут что и как.

Видео:Как строить сеченияСкачать

10 класс. Геометрия. Аксиомы стереометрии и их следствия.

10 класс. Геометрия. Аксиомы стереометрии и их следствия.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

1. Напоминание аксиом стереометрии и теорем, которые следуют из них

Аксиомы стереометрии и следствия из них устанавливают взаимоотношения между основными фигурами стереометрии: точкой, прямой и плоскостью.

Точка может лежать на прямой, может не лежать на прямой.

Прямая может принадлежать плоскости, может не принадлежать плоскости.

Плоскость может проходить через прямую, не проходить через нее, содержать точку, не содержать точку.

Подобные задачи мы решали для пирамиды и для параллелепипеда. Теперь мы будем решать задачи в общем виде.

Вспомним для этого сначала аксиомы и теоремы-следствия.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Иллюстрация аксиомы А1.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость , и притом только одна. Плоскость можно также обозначить через три точки АВС.

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Иллюстрация аксиомы А2. (Рис. 2.)

Аксиома 3 (А3).

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).

Иллюстрация аксиомы А3. (Рис. 3.)

Повторение теорем, которые следуют из аксиом стереометрии.

Теорема 1

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Иллюстрация теоремы 1. (Рис. 4.)

единственная

Теорема 2

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Иллюстрация теоремы 2. (Рис. 5.)

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

2. Решение задачи 1

Задача 1.

Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).

Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.

Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее .

Две разные точки А и В прямой с принадлежат плоскости . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.

Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости.

Видео:Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

3. Решение задачи 2

Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).

Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость

Прямая АВ целиком лежит в плоскости , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости .

Аналогично и с другими отрезками. Прямая ВС лежит в плоскости , потому что две ее точки В и С лежат в плоскости, значит, и отрезок ВС лежит в плоскости .

И аналогично, отрезок АС лежит в плоскости . Что и требовалось доказать.

Видео:№365. Вне плоскости параллелограмма ABCD взята точка О. Точка M — середина АВ, а точка КСкачать

4. Решение задачи 3

Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли 2 другие вершины параллелограмма в плоскости ?

Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.

Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка С, точка прямой АО, лежит в плоскости .

Аналогично, прямая ВО целиком лежит в плоскости , значит, точка D этой прямой тоже лежит в плоскости .

Ответ: Да, вершины С и D лежат в плоскости .

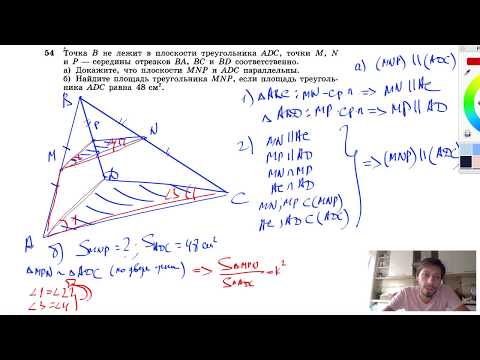
Видео:№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать

5. Решение задачи 4

Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.

Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.

Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через . Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости , в силу 2 аксиомы.

Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости . Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости , что и требовалось доказать.

Видео:🔴 Плоскость, проходящая через точки A, B и C ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

6. Решение задачи 5

Верно ли утверждение:

а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;

б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно.

б) Даны три точки окружности А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость .

Теперь докажем, что любая точка М окружности лежит в плоскости . Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости , потому что две ее точки А и D лежат в плоскости . Значит, и точка Мокружности лежит в плоскости . Значит, данное утверждение верно.

Видео:Как строить сечения параллелепипедаСкачать

7. Решение задачи 6

Точки А, В, С и D не лежат в одной плоскости (Рис. 11.).

а) Могут ли какие-то три из них лежать на одной прямой?

б) Могут ли прямые АВ и СD пересекаться?

а) Предположим, что любые три точки, например, А, В, С лежат на одной прямой. Тогда через эту прямую и точку Dпроходит плоскость, и все 4 точки лежат в этой плоскости, что противоречит условию;

б) Нет, так как через пересекающиеся прямые можно провести плоскость, а тогда, в этой плоскости содержатся все 4 точки, что противоречит условию.

Видео:🔴 Плоскость, проходящая через точки A, B и C ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

8. Решение задачи 7

а) Верно ли, что любые 3 точки лежат в одной плоскости?

Через 3 точки, если они не лежат на одной прямой, можно провести плоскость, и притом только одну, в силу аксиомы А1.

б) Верно ли, что любые 4 точки лежат в одной плоскости?

Через 3 точки можно провести плоскость, а 4 точку можно взять и в этой плоскости, и вне нее. Значит, ответ отрицательный.

в) Верно ли, что любые 4 точки не лежат в одной плоскости?

Приведем конкретный пример. Рассмотрим плоский четырехугольник, в плоскости этого четырехугольника лежат 4 точки. Итак, ответ на этот вопрос отрицательный, нет.

г) Верно ли, что через любые 3 точки проходит плоскость, и притом только одна?

Приведем пример. Возьмем 3 точки А, В, С, лежащие на одной прямой. Через них можно провести плоскость , плоскость . Через 3 точки, лежащие на одной прямой, можно провести бесконечное количество плоскостей.

9. Итоги урока

Итак, мы еще раз подытожили наши знания о стереометрии, а именно: прокомментировали три аксиомы, и два следствия из нее. И, кроме того, решили самые разнообразные задачи с использованием этих знаний.

Далее и аксиомы, и следствия будут использованы на следующих уроках при решении вопросов параллельности прямых и плоскостей.