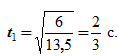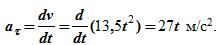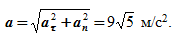Точка движется по окружности радиусом r с касательным ускорением (3 видео)

Точка движется по окружности радиусом r с касательным ускорением

2017-05-21
Материальная точка начинает двигаться по окружности радиуса $r = 10 см$ с постоянным касательным ускорением $a_ = 0,4 см/с^$. Через какой промежуток времени вектор ускорения а образует с вектором скорости $vec$ угол $beta$, равный: а) $60^$; б) $80^$ (рис.)? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус-вектор, проведенный из центра окружности к движущейся точке, если в начальный момент времени он направлен вертикально вверх? Движение происходит по часовой стрелке.

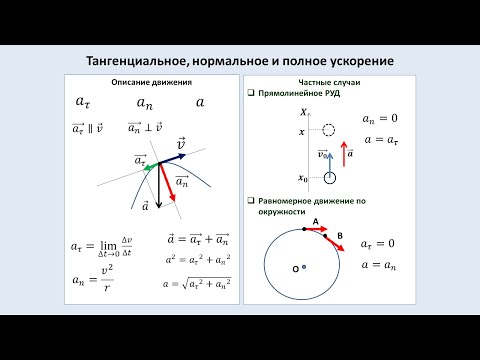
Материальная точка движется по окружности заданного радиуса. Поскольку движение ускоренное, скорость $v$ движущейся точки, а следовательно, и нормальное ускорение $a_ = v^/r$ непрерывно возрастают со временем. Касательное ускорение, по условию задачи, постоянно. Следовательно, вектор полного ускорения а со временем изменяется как по модулю, так и по направлению.

Постоянство касательного ускорения позволяет найти закон изменения со временем пути $s$, пройденного точкой, или угла поворота $phi$ радиус-вектора (см. рис.).

$a_ = dv/dt = const$.

Следовательно, мгновенная скорость движущейся точки (при $v_ = 0$)

Подставляя это выражение в формулу (1), находим

Тогда время и путь соответственно равны:

Угол поворота $phi = s/r$ изменяется со временем также по квадратичному закону:

а) При $beta_ = 60^$ ($tg beta_ = 1,73$), согласно выражениям (2) — (4), $t_ = 6,6 с; s_ = 8,7 см; phi_ = 0,87 рад$.
б) При $beta_ = 80^$ ($tg beta_ = 5,7$), согласно выражениям (2) — (4), $t_ = 12 с; s_ = 28 см; phi_ = 2,8 рад$.

Положения движущейся точки для найденных углов $phi_$ и $phi_$ и векторы $vec$ и $vec$ в эти моменты времени показаны на рис.

Содержание

iSopromat.ru
Задача
Решение
Точка движется по окружности радиусом r с касательным ускорением
🎥 Видео

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

iSopromat.ru

Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.

Видео:Центростремительное ускорение. 9 класс.Скачать

Задача

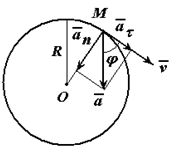
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).

Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t₁, когда скорость будет равна 6 м/с (рисунок 1.6).

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Решение

Дифференцируя s по времени, находим модуль вектора скорости точки

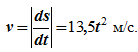
Подставляя в это выражение значение скорости, получим 6=13,5t₁ 2 , откуда находим

Касательное ускорение для любого момента времени равно

Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно

Модуль вектора полного ускорения точки равен

Угол между вектором полного ускорения и вектором скорости определим следующим образом:

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Точка движется по окружности радиусом r с касательным ускорением

Глава 7. Кинематика точки.

7.8. Ускорение точки при естественном способе задания движения.

7.8.1. Даны нормальное а_n = 2,5 м/с 2 и касательное а_τ = 1,5 м/с 2 ускорения точки. Определить полное ускорение точки. (Ответ 2,92)

7.8.2. Определить модуль ускорения точки, если его вектор а = 2,5n + 3,5τ, где n и τ — орты естественного триэдра. (Ответ 4,30)

7.8.3. Точка движется по криволинейной траектории с касательным ускорением а_τ = 1,4 м/с 2 . Определить нормальное ускорение точки в момент времени, когда ее полное ускорение а = 2,6 м/с 2 . (Ответ 2,19)

7.8.4. Определить нормальное ускорение точки в момент времени, когда ускорение точки а = 1,5 м/с 2 , а угол между векторами ускорения и скорости равен 65°. (Ответ 1,36)

7.8.5. Точка движется по окружности. Определить радиус окружности, если в момент времени, когда скорость v = 10 м/с, вектор ускорения и вектор скорости, равный по модулю 1,2 м/с, образуют угол 30°. (Ответ 167)

7.8.6. Дан график касательного ускорения а_τ = а_τ (t) движения точки по окружности радиуса 9 м. Определить полное ускорение в момент времени t = 2 с, если при t_o = 0 скорость точки v₀ = 0.
(Ответ 3,74)

7.8.7. Ускорение точки а = 1 м/с. Векторы ускорения и скорости образуют угол 45°. Определить скорость в км/ч, если радиус кривизны траектории ρ = 300 м. (Ответ 52,4)

7.8.8. Точка движется по окружности, радиус которой r = 200 м, с касательным ускорением 2 м/с 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда ее скорость v = 10 м/с. (Ответ 14,0)

7.8.9. Точка движется по окружности, радиус которой r = 50 м, со скоростью v = 2t. Определить модуль полного ускорения в момент времени t = 5 с. (Ответ 2,83)

7.8.10. Задано уравнение движения точки по криволинейной траектории: s = 0,2t 2 + 0,3t. Определить полное ускорение точки в момент времени t = 3 с, если в этот момент радиус кривизны траектории ρ = 1,5 м. (Ответ 1,55)

7.8.11. Определить скорость точки в момент времени, когда радиус кривизны траектории ρ = 5 м, касательное ускорение а_τ = 2 м/с 2 , а tgβ = 3, где β — угол между векторами скорости и ускорения точки (Ответ 5,48)

7.8.12. Даны графики ускорения а_τ = а_τ(t) и а_n = a_n(t). Определить, какой угол в градусах образует полное ускорение с направлением скорости в момент времени t = 3 с. (Ответ 56,3)

7.8.13. По окружности радиуса r = 6 м движется точка со скоростью v = 3t. Определить угол в градусах между ускорением и скоростью точки в момент времени t = 1 с. (Ответ 26,6)

7.8.14. Точка движется по окружности радиуса r = 9 м. Определить скорость точки в момент времени, когда касательное ускорение а_τ = 2 м/с 2 , а вектор полного ускорения а образует угол 70 o c касательной к траектории. (Ответ 7,03)

7.8.15. Дан график скорости v = v(t) движения точки по окружности радиуса 8 м. Определить полное ускорение в момент времени t = 4 с. (Ответ 2,24)

7.8.16. Точка движется но окружности радиуса r = 200 м из состояния покоя с постоянным касательным ускорением а_τ = 1 м/с 2 . Определить полное ускорение точки в момент времени t = 20 с. (Ответ 2,24)

7.8.17. Точка движется по окружности радиуса r = 2 м. Нормальное ускорение точки меняется согласно закону а_n = 2t 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t = 1 с. (Ответ 45)

7.8.18. Задан закон движении точки по траектории: s = 0,5t 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t₁ = 3 с, когда радиус кривизны ρ = 4 м. (Ответ 66,0)

7.8.19. По окружности радиуса r = 1м движется точка согласно уравнению s = 0,1t 3 . Определить полное ускорение точки в момент времени t = 2 с. (Ответ 1,87)

7.8.20. Точка движется по криволинейной траектории с касательным ускорением а_τ = 2 м/с 2 . Определить угол в градусах между векторами скорости и полного ускорении точки в момент времени t = 2 с, когда радиус кривизны траектории ρ = 4м, если при t₀ = 0 скорость точки v₀ = 0. (Ответ 63,4)

Сборник коротких задач по теоретической механике.
Кепе О.Э.

Книга состоит из 1757 заданий которые предназначены для бысторого
контроля знаний на занятиях и зачетах а также для допуска к экзамену.
Задачи имеют ответы.

Издательство «Высшая школа» 1989 Москва

Также решение задач Кепе можно скачать здесь:
Мобильное приложение для Андроид: