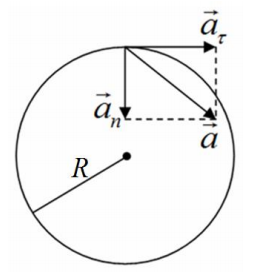
Точка движется по окружности радиусом R=4м.Закон её движения выражается уравнением S=A+Bt 2 , где A=8м; B=-2/с 2 . Найти момент времени t, когда нормальное ускорение точки an=9м/с 2 ; скорость v; тангенциальное at и полное a ускорение точки в этот момент.
Дано: R=4м, A=8м, B=-2/с 2 , an=9м/с 2 ,
Найти: t, v, at, a
Формула нормального (центростремительного) ускорения:
Здесь уточняем направление скорости v, определяем знак
Видео:Физика - движение по окружностиСкачать

Точка движется по окружности радиусом 4 закон ее движения
точка движется окружности радиусом
Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение аτ точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение an=2,7 м/с 2 .
Материальная точка движется по окружности радиуса R = 2 м согласно уравнению S = At+Bt 3 , где А = 8 м/с; В = –0,2 м/с 3 . Найти скорость v, тангенциальное at, нормальное an и полное а ускорения в момент времени t = 3 с.
Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением аτ. К концу четвертого оборота после начала движения линейная скорость точки v1 = 15 см/с Определите нормальное ускорение аn2 точки через t2 = 16 с после начала движения.
Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением аn = А + Bt + Ct 2 (А = 1 м/с 2 , В = 6 м/с 3 , С = 9 м/с 4 ). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t1 = 5 с после начала движения; 3) полное ускорение для момента времени t2 = 1 с.
Точка движется по окружности радиусом 4 м. Закон ее движения выражается уравнением s = 8 – 2t 2 , м. Определить: а) в какой момент времени нормальное ускорение точки будет равно 9 м/с 2 ; б) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени?
Точка движется по окружности радиусом R = 4 м так, что в каждый момент времени ее нормальное и тангенциальное ускорения равны по модулю. В начальный момент времени t = 0 скорость точки V0 = 0,2 м/с. Найти скорость точки в момент времени t1 = 10 c.
Точка движется по окружности радиусом R = 8 м. В некоторый момент времени нормальное ускорение точки равно 4 м/с 2 , вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60°. Найти линейную скорость и тангенциальное ускорение точки.
Точка движется по окружности радиусом 0,4 м согласно уравнению S = 2-cos2t. Определить нормальное ускорение точки в момент времени t = π/4 с?
Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аτ. Найти тангенциальное ускорение аτ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 79,2 см/с.
Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аτ. Найти нормальное ускорение аn точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 10 см/с.
Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением s = Ct 3 , где С = 0,1 см/с 3 . Найти нормальное an и тангенциальное aτ ускорения точки в момент, когда линейная скорость точки v = 0,3 м/с.
Точка движется по окружности радиусом R = 4 м. Начальная скорость v0 точки равна 3 м/с, тангенциальное ускорение аτ = 1 м/с 2 . Для момента времени t = 2 с определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения |Δr|; 3) среднюю путевую скорость ; 4) модуль вектора средней скорости | |.
Точка движется по окружности радиусом R = 2 м согласно уравнению ξ = At 3 , где A = 2 м/с 3 . В какой момент времени t нормальное ускорение аn точки будет равно тангенциальному аτ. Определить полное ускорение а в этот момент.
Материальная точка двигалась по окружности радиусом 2 м. Найдите путь и перемещение через 1/6 часть оборота, 1/4, 1/2 и полный оборот.
Точка движется по окружности радиусом 60 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 5 м/с.
Нормальное ускорение точки, движущейся по окружности радиусом 4 м, задаётся уравнением an = At 3 (A = 0,5 м/с 5 ). Определить: 1) тангенциальное ускорение точки в момент времени 5 c; 2) путь, пройденный точкой за время 5 с после начала движения; 3) полное ускорение для момента времени 1 с.
Точка движется по окружности радиусом R = 1,20 м. Уравнение движения точки имеет вид: φ = At + Bt 3 , где А = 0,500 рад/с, В = 2,50 рад/с 3 . Определить тангенциальное аτ, нормальное ап и полное а ускорение точки в момент времени t = 0,954 с.
Точка движется по окружности радиуса R = 0,5 м с постоянным касательным ускорением 2 м/с 2 из состояния покоя. Определить нормальное и полное ускорения точки в момент времени t = 1 с.
Материальная точка движется по окружности радиусом R = 4 м. Закон ее движения описывается уравнением ξ = A+Bt 2 , где A = 8 м, B = –2 м/с 2 , а ξ отсчитывается вдоль окружности. Найти момент времени, когда нормальное ускорение точки равно 9 м/с 2 , а также скорость, тангенциальное и полное ускорения точки в этот момент времени.
Материальная точка движется по окружности радиусом R = 1 м. Зависимость угла поворота от времени имеет вид φ = At 4 , где A = 1 рад/с 4 . Определить линейное ускорение материальной точки через секунду после начала движения, а также угол между линейным ускорением и радиусом окружности в этот момент времени.
Материальная точка движется по окружности радиуса R = 2 м. Закон ее движения описывается уравнением ξ(t) = At 2 + Bt 3 , где А = 3 м/с 2 , В = 1 м/с 3 , а координата ξ(t) отсчитывается вдоль окружности. Найти момент времени, когда тангенциальное ускорение точки равно 18 м/с 2 , а также нормальное и полное линейное ускорение точки в этот момент времени.
Материальная точка движется по окружности радиуса R, причем φ = ωt (φ – угол между радиус-вектором точки, проведенным из некоторой точки А окружности, и прямой, соединяющей точку А и центр окружности; ω — константа). Найти тангенциальную и нормальную составляющие скорости и ускорения точки.
Точка движется по окружности радиусом 79 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 3 м/с.
Точка движется по окружности радиусом R = 0,1 м с постоянным тангенциальным ускорением. Найти ускорение точки через 10 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 0,8 м/с.
Видео:Центростремительное ускорение. 9 класс.Скачать

Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt2 , где А = 8 м, В = -2 м/с 2 . Определить момент времени t, когда нормальное ускорение n а точки равно 9 м/с2
| 🎓 Заказ №: 21966 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt2 , где А = 8 м, В = -2 м/с 2 . Определить момент времени t, когда нормальное ускорение n а точки равно 9 м/с2 . Найти скорость , тангенциальное и полное a ускорения точки в тот же момент времени t .
Решение Уравнение для скорости движения по окружности получается из заданного уравнения движения дифференцированием по времени. Bt dt d A Bt dt dS 2 2 (1) Производная от линейной скорости по времени дает выражение для модуля тангенциального ускорения. B dt d Bt dt d a 2 2 (2) Скорость движения по окружности связана с нормальным ускорением соотношением

Научись сам решать задачи изучив физику на этой странице:
|
Услуги:
|
Готовые задачи по физике которые сегодня купили:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💥 Видео
Точка движется по окружности радиусом R=2см. Волькенштейн 1.47Скачать

Кинематика. Движение по окружности. Урок 4Скачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Материальная точка движется по окружности радиусом R с постоянной по модулю скоростьюСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Материальная точка равномерно движется по окружности, центр которой находится в начале O - №22689Скачать
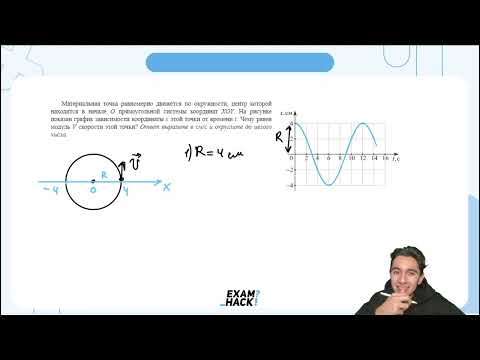
Физика Шарик равномерно движется по окружности радиусом 3 м, совершая полный оборот за 10 сСкачать
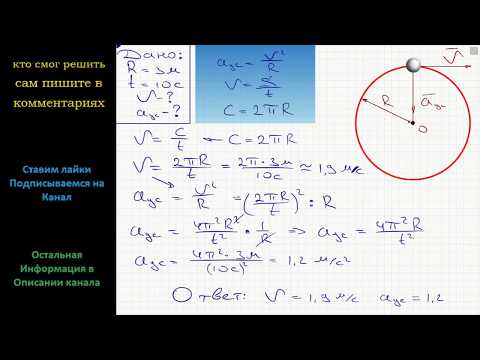
Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Урок 90. Движение по окружности (ч.2)Скачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Урок 89. Движение по окружности (ч.1)Скачать

Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Движение тел по окружностиСкачать