Tgx больше 0 на окружности (5 видео) | Курс школьной геометрии

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Содержание

Узнать ещё
a»>tgx>a
tan(x)>=0 (неравенство)
Шаг 1. Введите неравенство
Решение
📽️ Видео

Видео:Решить неравенство tg xСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Как решать тригонометрические неравенства?Скачать

a»>tgx>a

Рассмотрим решение тригонометрических неравенств вида tgx>a и tgx

Для решения нам потребуется чертеж единичной окружности и линия тангенсов . Радиус единичной окружности равен 1, поэтому, откладывая на линии тангенсов отрезки, длина которых равна радиусу, получаем соответственно точки, в которых тангенс равен 1, 2, 3 и т.д., а вниз — -1,-2,-3 и т.д.

1) tgx>a

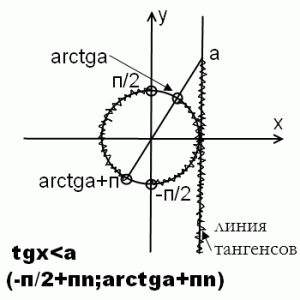
На линии тангенсов значениям тангенсов, большим a, соответствует часть, расположенная выше точки а. Заштриховываем соответствующий луч. Теперь проводим прямую через точку О — начало отсчета- и точку а на линии тангенсов. Она пересекает окружность в точке arctg a. Соответственно, на окружности решению неравенства tgx>a соответствует дуга от точки arctg a до п/2. Чтобы учесть все решения (а их с учетом периодичности тангенса — бесконечное множество), к каждому концу интервала прибавляем пn, где n — целое число (n принадлежит Z).

Для решения неравенства tgx>a вполне достаточно полуокружности от -п/2 до п/2. Но если требуется найти, к примеру, решение системы неравенств с тангенсом и синусом, то нужна вся окружность.

Если неравенство нестрогое, точку с arctg a включаем в ответ (на рисунке ее заштриховываем, в ответ записываем с квадратной скобкой). Точка п/2 в ответ никогда не включается, поскольку не входит в область определения тангенса (точка выколотая, скобка круглая).

2) tgx>-a

Чтобы решить неравенство tgx>-a, рассуждаем так же как и для неравенства tgx>a. Поскольку arctg (-a)=-arctg a, только этим и отличается ответ.

В этом случае решению неравенства tgx

4) tgx Светлана Иванова, 17 Окт 2012

Видео:Тригонометрическая окружность tg x и ctg xСкачать

tan(x)>=0 (неравенство)

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Шаг 1. Введите неравенство

Укажите решение неравенства: tan(x)>=0 (множество решений неравенства)

Решение

Дано неравенство:
$$tan geq 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$tan = 0$$
Решаем:
Дано уравнение
$$tan = 0$$
— это простейшее тригонометрическое ур-ние

Получим:
$$tan = 0$$
Это ур-ние преобразуется в
$$x = pi n + operatorname$$
Или
$$x = pi n$$
, где n — любое целое число
$$x_ = pi n$$
$$x_ = pi n$$
Данные корни
$$x_ = pi n$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_ leq x_$$
Возьмём например точку
$$x_ = x_ — frac$$
=
$$pi n + — frac$$
=
$$pi n — frac$$
подставляем в выражение
$$tan geq 0$$
$$tan<left (pi n — frac right )> geq 0$$