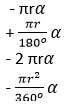Тест по геометрии 8 класс окружность центральный и вписанный

Тесты по геометрии 8 класс. Тема: «Центральный и вписанный углы»

Правильный вариант ответа отмечен знаком +

1. Угол называется центральным, если его вершина… Продолжите определение:

— лежит внутри окружности

— лежит на окружности

+ совпадает с центром окружности

— лежит на диаметре

2. Чему равна градусная мера двух дуг с общими концами?

3. В каком случае дуга называется полуокружностью?

+ если отрезок, который соединяет концы дуги, является диаметром

— если на нее опирается вписанный угол

— если на один из концов дуги опирается радиус окружности

— если отрезок, соединяющий концы дуги, является хордой

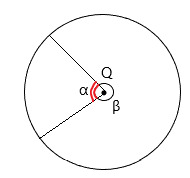
4. Какой из углов на представленном рисунке будет центральным, если Q – центр окружности?

+ угол α и угол β

— ни один из углов

5. Градусная мера центрального угла равна градусной мере … Вставьте пропущенное утверждение:

+ градусной мере дуги, на которую он опирается

— градусной мере прямого угла

— градусной мере вписанного угла, опирающегося на ту же дугу

— градусной мере дуги, на которую опирается диаметр окружности

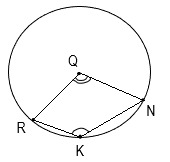
6. На рисунке представлена окружность с центром в точке Q. Известно, что угол RKN=130°. Необходимо найти величину угла RQN.

7. Выберите формулу для нахождения длины дуги, на которую опирается центральный угол, если центральный угол равен α, а радиус равен r:

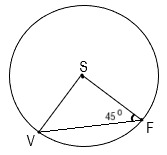
8. Треугольник VSF вписан в окружность с центром S. Угол SFV=45°, необходимо найти центральный угол VSF.

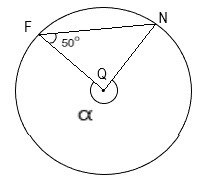
9. Найдите угол α, если известно, что угол QFN=50°, а точка Q является центром окружности.

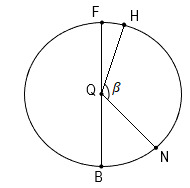
тест 10. Отрезок FB является диаметром окружности. Центральный угол FQH=32°, угол BQN=47°. Найдите угол β.

11. Углом, вписанным в окружность, называют угол, вершина которого …, а его стороны пересекают окружность. Вставьте пропущенные слова.

— лежит в точке, которая является центром окружности

— расположена внутри окружности

— является серединой диаметра окружности

+ лежит на окружности

12. Как измеряется вписанный угол?

— он равен произведению радиуса и дуги, на которую опирается

+ он равен половине центрального угла окружности, который опирается на ту же дугу, что и вписанный угол

— он равен градусной мере дуги, на которую опирается

— он равен сумме углов, образованных его сторонами и диаметром окружности

13. Выберите верное утверждение:

— на одной дуге можно построить только один центральный и один вписанный угол

+ вписанный угол измеряется половиной градусной меры дуги, на которую опирается

— центральный и вписанный углы, построенные на одной дуге, равны между собой

— если центральный угол тупой, то и вписанный, опирающийся на эту же дугу, также обязательно тупой

14. Чем отличается вписанный угол от центрального?

— сторона центрального угла проходит через центр окружности, а сторона вписанного угла пересекает окружность

— вписанный угол может опираться на диаметр, а центральный – нет

— вписанный угол измеряется по формулам вписанного треугольника, а центральный – дугой, на которую опирается

+ вершина центрального угла лежит в центре окружности, а вершина вписанного угла – на окружности

15. Вписанные углы, которые опираются на одну дугу… Закончите утверждение:

+ равны между собой

— проходят через центр окружности

— равны центральному углу, опирающемуся на ту же дугу

16. Известно, что два вписанных угла опираются на одну и ту же хорду, а также находятся по разные стороны от нее. Чему равна сумма этих вписанных углов?

17. На одну дугу может опираться несколько вписанных углов. Сколько центральных углов опирается на эту же дугу?

— столько же, сколько и вписанных углов

— на один меньше, чем вписанных

18. Если вписанный угол опирается на диаметр, следовательно, он:

— равен градусной мере соответствующего центрального угла

— измеряется градусной мерой дуги, на которую опирается

19. Какое из следующих утверждений верно:

+ любой прямой вписанный угол опирается на полуокружность

— если угол центральный, то он не может быть больше 180

— невозможно построить центральный угол, опирающийся на диаметр

— все утверждения неверны

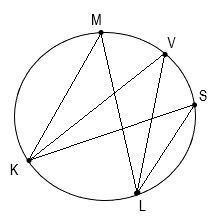
тест-20. Найдите сумму углов KML, KVL и KSL, если дуга KL равна 50°.

21. Известно, что центральный угол окружности равен 118°. Необходимо найти вписанный угол, опирающийся на ту же дугу, что и центральный.

22. Вписанный и центральный углы опираются на одну дугу. Известно, что вписанный угол на 20° меньше, чем центральный. Найдите центральный угол окружности.

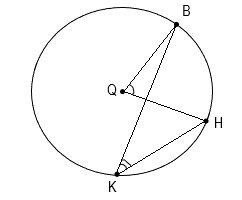
23. Необходимо найти сумму градусных мер углов BQH и BKH, если известно, что Q – центр окружности, а дуга BH равна 80°.

24. В окружности с центром Q угол KQH является центральным и равен 70°. Точка R лежит на окружности внутри угла KQH. Найдите угол KRH.

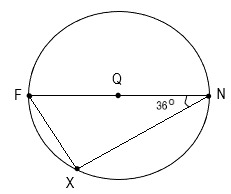
25. Дана окружность с центром Q и диаметром FN. Угол FNX=36°. Необходимо найти градусную меру дуги NX.

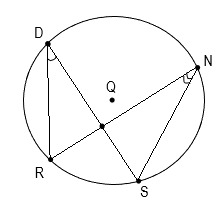
26. Дана окружность с вписанными углами RDS и RNS. Сумма их градусных мер составляет 80°. Необходимо найти градусную меру дуги RS.

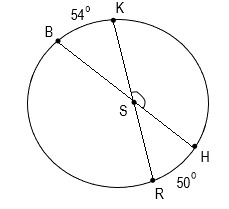
27. Точка S не является центром окружности. Градусная мера дуги BK составляет 54°, градусная мера дуги RH составляет 50°. Необходимо найти угол KSH.

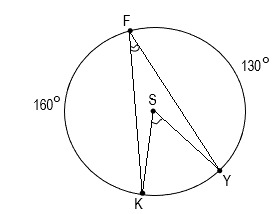
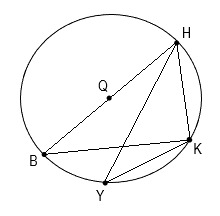
28. Дана окружность с центром в точке S. Если дуга FK=160°, а дуга FY=130°, тогда:

— дуга KY= 35°, угол KSY=35°, угол KFY=70°

— дуга KY= 70°, угол KSY=35°, угол KFY=70°

+ дуга KY= 70°, угол KSY=70°, угол KFY=35°

— дуга KY= 35°, угол KSY=70°, угол KFY=35°

29. В окружность с центром Q вписаны два треугольника HBK и HYK. Необходимо найти угол BHK, если известно, что угол HYK=38°, а сторона BH является диаметром.

тест_30. Углы KPF и KMF опираются на одну хорду с разных сторон. Найдите градусную меру углов, если известно, что угол KPF меньше угла KMF в 2 раза.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тест по теме: «Вписанная и описанная окружности» (8 класс)
тест по геометрии (8 класс) на тему

Тест по теме: «Вписанная и описанная окружности» (8 класс)

Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Скачать:

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Предварительный просмотр:

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Угол A четырехугольника ABCD, вписанного в окружность, равен 48°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
6. В любом вписанном четырехугольнике сумма противолежащих углов равна

а) 360; б) 180; в) 90.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1) AB+BC=AD+CD; 3) AB+CD=BC+AD;

2) AB+AD=BC+CD; 4) AD·BC=AB·CD .

8.Описанная около треугольника окружность изображена на рисунке:

9.Вписанная в четырехугольник окружность изображена на рисунке:

10.В треугольник можно вписать _______________________________.

11.Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. В любом описанном четырехугольнике суммы противолежащих сторон: а) равны; б) равны радиусу; в) равны периметру.
6. Вписанная в треугольник окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать __________________________.
2. Около окружности описана трапеция, периметр которой равен 76. Найдите длину её средней линии.
3. Угол A четырехугольника ABCD, вписанного в окружность, равен 100°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

11.Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

Видео:ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 классСкачать

Тест по геометрии «Центральные и вписанные углы окружности» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Центральные и вписанные углы

§ 9. Центральные и вписанные углы

1. Вершины треугольника АВС лежат на окружности, угол А равен 70 градусов , угол С равен 30 градусов. Чему равна дуга АС ? (Начертите рисунок).

1. Точки А, В, С лежат на окружности с центром в точке О. Дуги АВ : АС = 2 : 3 , угол ВАС равен 55 градусов . Чему равен угол АОС ? (Начертите рисунок)

1. Точки А, В, С, К (именно в этом порядке) лежат на окружности так, что АК- это диаметр , угол СКВ равен 25 градусов , угол САК равен 20 градусов. Найдите угол АКВ ? (Начертите рисунок) A) 50

Выберите верное утверждение:

A) Вписанный угол равен дуге, на которую он опирается

B) Вписанный угол равен половине дуги, на которую он опирается

C) Вписанный угол равен 90 градусов

D) Вписанный угол равен центральному углу

Центральный угол окружности — это .

A) угол с вершиной , лежащей на окружности

B) угол с вершиной в центре дуги

C) угол с вершиной в центре окружности

D) угол равный вписанному углу.

Чему равен центральный угол?

A) Половине дуги ,на которую он опирается

B) Градусной мере дуги ,на которую он опирается

C) равен вписанному углу

D) равен 90 градусов

Вершины треугольника АВС лежат на окружности ,так что сторона АС является диаметром этой окружности. Найдите угол АВС ?

Точки А,В,С,К лежат на окружности (именно в этом порядке) . Угол АВК равен 60 градусов . Чему равен угол АСК ?

Угол АОС — центральный угол окружности с центром в точке О и равен 40 градусов. Найти угол ОАС ?

Вершины М,С,Н,Р лежат на окружности ( именно в этом порядке). Угол МСР равен 70 градусов ,а дуга НР равна 120 градусов. Найти угол МРН ?

Правильные ответы, решения к тесту:

Правильный ответ — D Вопрос №2

Правильный ответ — B

Правильный ответ — B

Правильный ответ — B Вопрос №5

Правильный ответ — C Вопрос №6

Правильный ответ — B

Правильный ответ — B Вопрос №8

Правильный ответ — D Вопрос №9

Правильный ответ — C Вопрос №10

Правильный ответ — A

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 673 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 537 391 материал в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 9. Центральные и вписанные углы

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 18.09.2021
• 155
• 3

• 18.09.2021
• 102
• 1

• 18.09.2021
• 42
• 1

• 18.09.2021
• 277
• 20

• 18.09.2021
• 94
• 2

• 18.09.2021
• 1123
• 132

• 18.09.2021
• 65
• 1

• 17.09.2021
• 88
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 18.09.2021 621
• PDF 36 кбайт
• 42 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Шкенева Жанна Евгеньевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 2 месяца
• Подписчики: 0
• Всего просмотров: 3910
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Школьники в Пензенской области с 7 по 14 февраля уйдут на внеплановые каникулы

Время чтения: 2 минуты

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Рязанских школьников с 5 по 8 классы переведут на дистанционное обучение

Время чтения: 1 минута

В Курганской области школьников переведут на дистанционное обучение с 4 февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Центральные и вписанные углы - геометрия 8 классСкачать

Вписанная окружность. Видеоурок по геометрии 8 классСкачать

Геометрия 8 класс : Решение задач на центральные и вписанные углыСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 8 класс. Центральный и вписанный уголСкачать

ГЕОМЕТРИЯ 8 класс : Центральные и вписанные углыСкачать

Углы, вписанные в окружность. 9 класс.Скачать

8 класс. Решаем задачи на центральные и вписанные углы | Часть 1Скачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Вписанный угол в окружность ❤️ #геометрияСкачать