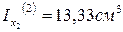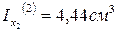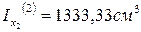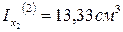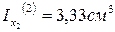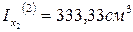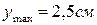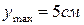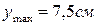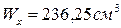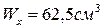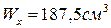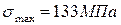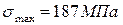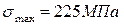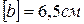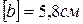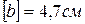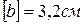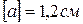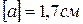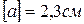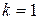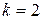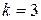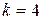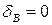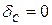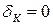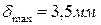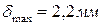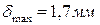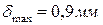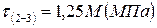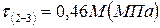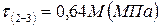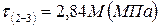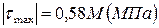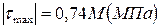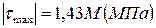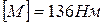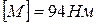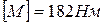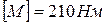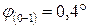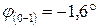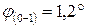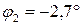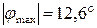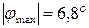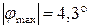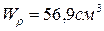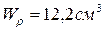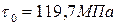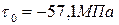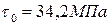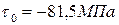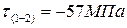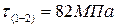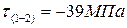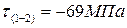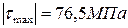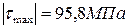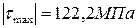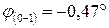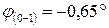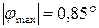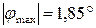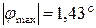Тесты к теме 1.1 «Построение эпюры продольной силы»
Вариант 1
1. На какое количество участков надо поделить данный стержень для построения эпюры N?
2. В каких сечениях данного стержня на эпюре N будут скачки?
1. В сечениях, где приложены сосредоточенные силы
2. В сечениях, где меняется размер сечения
3. В сечениях, где начинается и кончается распределенная нагрузка
4. В сечениях, где приложены сосредоточенные силы и где начинается и кончается распределенная нагрузка
3. На каких участках эпюры N для данного стержня будут прямые параллельные базе эпюры?
1. На участках ВС и ЕН
2. На участках CD и DE
3. На участках ВС и СD
4. На участках DE и EH
5. На всех участках
4. На каких участках эпюры N для данного стержня будут наклонные прямые?
1. На всех участках
2. Таких участков нет
3. На участках CD и DE
4. На участках ВС и СВ
5. На участках DE и EH
5. Выберите правильную эпюру N для данного стержня.
Вариант 2
1. На какое количество участков надо поделить данный стержень для построения эпюры N?
2. В каких сечениях данного стержня на эпюре N будут скачки?
4. Во всех сечениях стержня
3. На каких участках эпюры N для данного стержня будут прямые параллельные базе эпюры?
1. На всех участках
2. На участках ВС и ЕН
3. На участках CD и DE
4. На участках ВС, СD и EH
5. На участке DЕ
4. На каких участках эпюры N для данного стержня будут наклонные прямые?
1. На всех участках
2. На участках ВС и ЕН
3. На участках CD и DE
4. На участках ВС, СD и EH
5. На участках DE и EH
5. Для данного стержня выберите правильную эпюру N.
Тесты к теме 1.2 «Построение эпюры внутреннего крутящего момента»
Вариант 1
1. На какое количество участков надо поделить данный вал для построения эпюры Мz?
2. В каких сечениях данного вала на эпюре Mz будут скачки?
1. Во всех сечениях
3. На каких участках эпюры Mz для данного вала будут прямые параллельные базе?
1. На всех участках эпюры
2. На участке CD
3. Таких участков нет
4. На участке BС
4. На каких участках эпюры Mz для данного вала будут наклонные прямые?
1. На всех участках эпюры
2. На участке CD
3. Таких участков нет
4. На участке BC
5. Для данного вала выберите верную эпюру Mz.
Вариант 2
1. На какое количество участков надо поделить данный вал для построения эпюры Мz?
2. В каких сечениях данного вала на эпюре Mz будут скачки?
1. Во всех сечениях
3. На каких участках эпюры Mz для данного вала будут прямые параллельные базе?
1. На всех участках эпюры
3. Таких участков нет
4. На участках AB, DE
5. На участке CD
4. На каких участках эпюры Mz для данного вала будут наклонные прямые?
1. На всех участках эпюры
3. Таких участков нет
4. На участках АB, ЕН
5. Выберите верную эпюру Mz для данного вала
Тесты к теме 1.3 «Построение эпюр внутренней поперечной силы и изгибающего момента при прямом изгибе балок»
Вариант 1
1. На какое количество участков надо поделить данную балку для построения эпюр Qy и Mz?
2. В каких сечениях данной балки будут скачки на эпюре Qy?
1. В сечениях А и D
2. В сечениях В и С
4. Скачков не будет ни в одном сечении
3. В каких сечениях данной балки будут скачки на эпюре Мх?
1. В сечениях А и В
2. В сечениях В и С
3. В сечениях В и D
4. Скачков не будет ни в одном сечении
4. На каких участках данной балки будут прямые параллельные базе на эпюре Qy?
1. На участках АВ и CD
2. На участке ВС
3. На всех участках
4. Ни на одном участке
5. На каких участках данной балки будут наклонные прямые на эпюре Qy?
1. На участке ВС
2. На участках АВ и CD
3. На всех участках балки
4. Ни на одном участке
6. На каких участках данной балки будут прямолинейные зависимости на эпюре Мх?
1. На участках АВ и CD
2. На участке ВС
3. На всех участках
4. Ни на одном участке
7. На каких участках данной балки будут параболические зависимости на эпюре Мх?
1. На участке ВС
2. На участках АВ и CD
3. На всех участках
4. Ни на одном участке
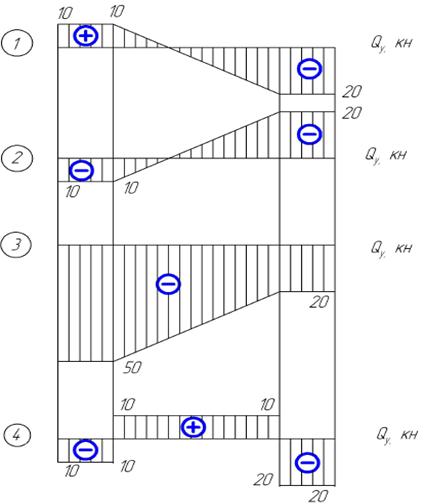
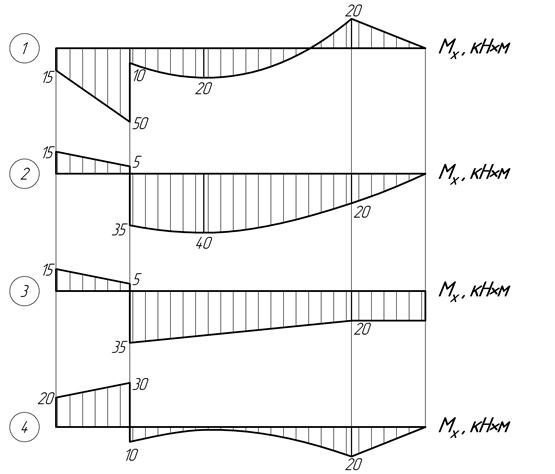
8. Для данной балки выберите верную эпюру Qy
9. Для данной балки выберите верную эпюру Мх
Вариант 2
1. На какое количество участков надо поделить данную балку для построения эпюр Qy и Mz?
2. В каких сечениях данной балки будут скачки на эпюре Qy?
4. Скачков не будет ни в одном сечении
3. В каких сечениях данной балки будут скачки на эпюре Мх?
1. Скачков не будет ни в одном сечении
2. В сечениях С и В
3. В сечениях В и D
4. На каких участках данной балки будут прямые параллельные базе на эпюре Qy?
1. На участках АВ и DН
2. На участке СВ
3. На всех участках
4. Ни на одном участке
5. На каких участках данной балки будут наклонные прямые на эпюре Qy?
1. На всех участках балки
2. На участках АB и DH
3. На участке ВС и CD
4. Ни на одном участке
6. На каких участках балки будут прямолинейные зависимости на эпюре Мх?
1. Ни на одном участке
2. На участке ВC
3. На всех участках
4. На участках АB и DH
7. На каких участках балки будут параболические зависимости на эпюре Мх?
1. На участках АВ и DН
2. На участке ВC и CD
3. На всех участках
4. Ни на одном участке
8. Для данной балки выберите верную эпюру Qy.
9. Для данной балки выберите верную эпюру Мх.
Тесты к теме 2 «Расчет на прочность и жесткость при растяжении-сжатии»
Вариант 1
Задан ступенчатый стержень круглого поперечного сечения с построенной эпюрой внутренней продольной силы N:
Площадь поперечного сечения участков ВС и ЕН стержня равна 2 см 2 , а участков CD и DE равна 4 см 2 . Материал стержня – Ст 3 с допускаемым напряжением 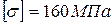
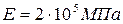
1. Определите, какое сечение данного стержня самое опасное.
1. Все сечения участков ВС и ЕН равноопасны
2. Сечения С и Е участков CD и DE
3. Сечения С и Е участков ВC и EН
2. Чему равно максимальное по абсолютной величине напряжение, возникающее в сечениях данного стержня?
3. Чему равно минимальное напряжение в сечениях данного стержня?
4. Определите величину и направление перемещения сечения С данного стержня, приняв за неподвижное сечение В.
1. 0,5 мм к сечению В
2. 0,5 мм от сечения В
3. 1 мм к сечению В
4. 1 мм от сечения В
5. Определите минимальный диаметр данного стержня из условия прочности.
Вариант 2
Задан стержень круглого поперечного сечения с построенной эпюрой внутренней продольной силы N:
Площадь поперечного сечения всех участков стержня одинакова и равна 2 см 2 . . Материал, из которого изготовлен стержень, Ст 3 с допускаемым напряжением 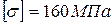
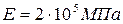
1. Определите, какое сечение данного стержня самое опасное.
2. Чему равно максимальное по абсолютной величине напряжение, возникающее в сечениях данного стержня?
3. Чему равно минимальное напряжение, возникающее в сечениях данного стержня?
4. Определите величину и направление перемещения сечения Е данного стержня, приняв за неподвижное сечение Н.
1. 0,625 мм к сечению Н
2. 0,625 мм от сечения Н
3. 0,25 мм к сечению Н
4. 0,25 мм от сечения Н
5. Определите диаметр данного стержня из условия прочности.
Тесты к теме 3 «Геометрические характеристики плоских сечений»
Вариант 1
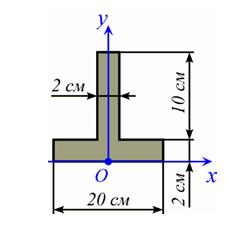
Задано сложное сечение, состоящее из двух прямоугольников:
Обозначим верхний прямоугольник №1, а нижний №2.
1. Чему равны координаты центров тяжести прямоугольников y1 и y2 в заданной системе координат xOy?
1. у1= 2см, у2= 6см
2. у1= 1см, у2= 7см
3. у1= –6см, у2= 0см
4. у1= 7см, у2= 1см
2. Чему равны статические моменты первого и второго прямоугольников относительно оси х?
1. Sx (1) = –50 см 3 , Sx (2) =100 см 3
2. Sx (1) =40см 3 , Sx (2) =120 см 3
3. Sx (1) =140 см 3 , Sx (2) =40 см 3
4. Sx (1) =70см 3 , Sx (2) =10см 3
3. Чему равна координата центра тяжести данного сложного сечения yС в заданной системе координат xOy?
4. Чему равны моменты инерции прямоугольников относительно собственных главных центральных осей х1 и х2?
1. 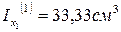
2. 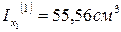
3. 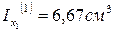
4. 
5. Чему равны расстояния между центром тяжести всего сечения и центрами тяжести каждого прямоугольника b1 и b2, соответственно?
1. b1=4см 3 b2=2 см 3
2. b1=3см 3 b2=3см 3
3. b1=2см 3 b2=4см 3
4. b1=5см 3 b2= 1см 3
6. Чему равны главные центральные моменты инерции сложного сечения?
1. Ix=660см 4 Iy=1340см 4
2. Ix=840см 4 Iy=1160см 4
3. Ix=1280см 4 Iy=960см 4
4. Ix=1060см 4 Iy=740см 4
Вариант 2
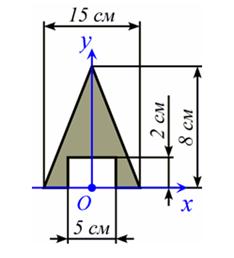
Задано сложное сечение, состоящее из треугольника и прямоугольной выемки.
Обозначим треугольник простейшей фигурой №1, а прямоугольник №2.
1. Чему равны координаты центров тяжести треугольника y1 и прямоугольника y2 в заданной системе координат xOy?
2. Чему равны статические моменты треугольника и прямоугольника относительно оси х?
1. Sx (1) =-180 см 3 , Sx (2) =0 см 3
2. Sx (1) =240см 3 , Sx (2) =10 см 3
3. Sx (1) =160 см 3 , Sx (2) =10 см 3
4. Sx (1) =320см 3 , Sx (2) =20см 3
3. Чему равна координата центра тяжести данного сложного сечения yС в заданной системе координат xOy?
4. Чему равны моменты инерции треугольника и прямоугольника относительно собственных главных центральных осей х1 и х2?
1. 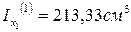
2. 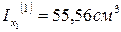
3. 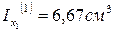
4. 
5. Чему равны расстояния между центром тяжести всего сечения и центрами тяжести каждого прямоугольника b1 и b2, соответственно?
1. b1=7/3см 3 b2=4см 3
2. b1=4/3см 3 b2=3см 3
3. b1=1/3см 3 b2=2см 3
4. b1=5см 3 b2= 1см 3
6. Чему равны главные центральные моменты инерции сложного сечения?
1. Ix=660см 4 Iy=1340см 4
2. Ix=263,33см 4 Iy=583,33см 4
3. Ix=1280см 4 Iy=960см 4
4. Ix=846,67см 4 Iy=537,33см 4
Тесты к теме 4 «Расчет на прочность балок при прямом изгибе»
Вариант 1
Балка с жестким защемлением, изготовленная из пластичного материала с допускаемым напряжением 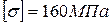
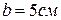
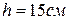
1. Какое сечение балки является наиболее опасным?
2. Где в опасном сечении расположена зона растянутых волокон относительно нейтральной линии?
1. Выше нейтральной линии
2. Ниже нейтральной линии
3. Где расположены опасные точки в опасном сечении?
1. На верхней и нижней сторонах прямоугольника
2. На левой и правой сторонах прямоугольника
3. На нейтральной линии
4. На диагоналях прямоугольника
4. Чему равно расстояние от нейтральной линии до наиболее удаленных точек сечения?
1.
2.
3.
4.
5. Чему равен осевой момент сопротивления 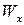
1.
2.
3.
4.
6. Чему равна величина максимального нормального напряжения в опасных точках опасного сечения?
1.
2.
3.
4.
7. Выполняется ли условие прочности для заданной балки?
2. Не выполняется
8. Чему равно минимально допустимое значение стороны прямоугольника 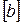
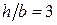
1.
2.
3.
4.
Вариант 2
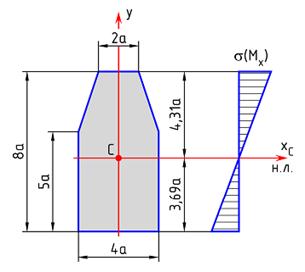
Балка на двух шарнирных опорах, изготовленная из хрупкого материала с допускаемыми напряжениями 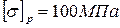
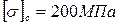
Поперечное сечение балки сложное, размеры которого заданы в долях параметра а. Положение центра тяжести С определено, хС – нейтральная линия сечения. Момент инерции сечения 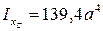
1. Какое сечение балки является наиболее опасным?
2. Где в опасном сечении расположена зона растянутых волокон относительно нейтральной линии?
1. Выше нейтральной линии
2. Ниже нейтральной линии
3. Рационально ли расположено сечение или его нужно повернуть на 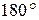
1. Сечение расположено рационально
2. Сечение расположено нерационально, его нужно повернуть на
4. Какое волокно является наиболее опасным при рациональном расположении сечения?
1. Растянутое волокно
2. Сжатое волокно
5. Чему равен из условия прочности характерный размер сечения 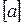
1.
2.
3.
4.
Тесты к теме 5 «Расчет на жесткость балок при прямом изгибе»
Вариант 1
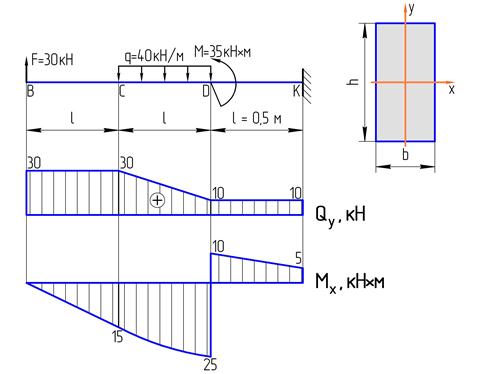
Балка с жестким защемлением нагружена известной системой внешних поперечных сил и изгибающих моментов. Поперечное сечение балки прямоугольное со сторонами 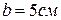
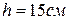
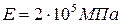
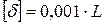
1. Чему равно количество участков перемножения k при определении перемещения в сечении В?
1.
2.
3.
4.
2. Чему равно перемещение сечения В?
1.
2. 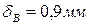
3. 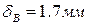
4. 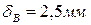
3. Чему равно количество участков перемножения k при определении перемещения в сечении С?
1.
2.
3.
4.
4. Чему равно перемещение сечения С?
1.
2. 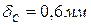
3. 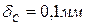
4. 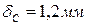
5. Чему равно количество участков перемножения k при определении перемещения в сечении D?
1.
2.
3.
4.
6. Чему равно перемещение сечения D?
1.
2. 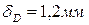
3. 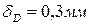
4. 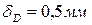
7. Чему равно перемещение сечения K?
1.
2. 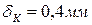
3. 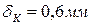
4. 
8. Какое сечение балки имеет наибольшее перемещение?
9. Чему равен наибольший прогиб балки?
1.
2.
3.
4.
10. Выполняется ли условие жесткости?
2. Не выполняется
Вариант 2
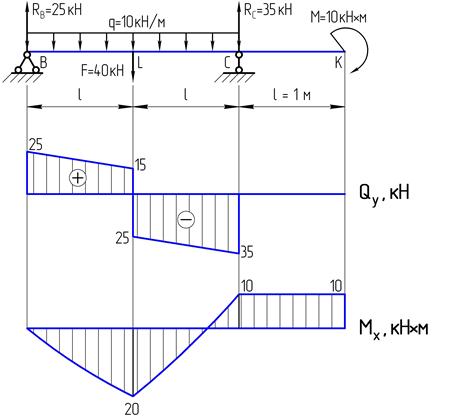
Балка на двух шарнирных опорах нагружена известной системой внешних поперечных сил и изгибающих моментов.
Поперечное сечение балки сложное, момент инерции сечения 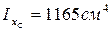
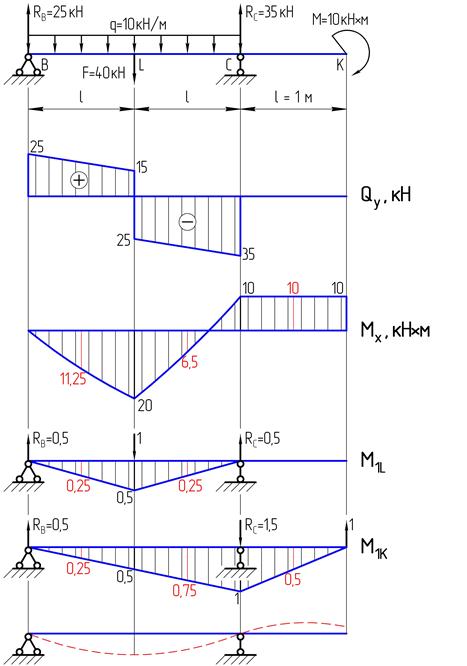
Рассчитать балку на жесткость, используя предоставленный графический материал. Принять: 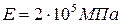
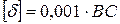
1. Чему равно количество участков перемножения k при определении перемещения в сечении L?
1.
2.
3.
4.
2. Чему равно перемещение сечения L?
1.
2. 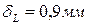
3. 
4. 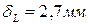
3. Чему равно количество участков перемножения k при определении перемещения в сечении K?
1.
2.
3.
4.
4. Чему равно перемещение сечения K?
1.
2. 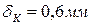
3. 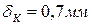
4. 
5. Чему равно перемещение сечения B?
1.
2. 
3. 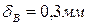
4. 
6. Чему равно перемещение сечения C?
1. 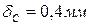
2.
3. 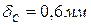
4. 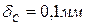
7. Какое сечение балки имеет наибольшее перемещение?
8. Чему равен наибольший прогиб балки?
1.
2.
3.
4.
9. Выполняется ли условие жесткости?
2. Не выполняется
Тесты к теме 6 «Расчет на прочность и жесткость при кручении вала круглого поперечного сечения»
Вариант 1
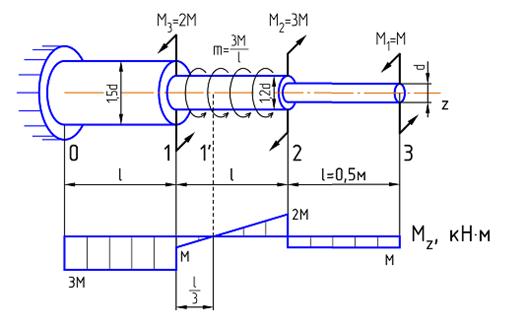
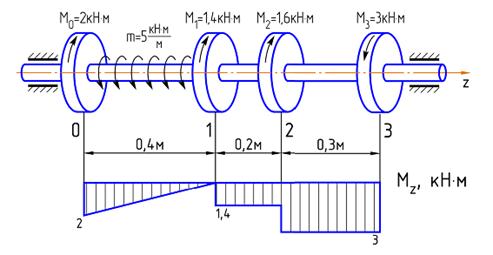
Ступенчатый вал круглого поперечного сечения, изготовленный из малоуглеродистой стали Ст3, нагружен системой внешних крутящих моментов, заданных в долях параметра М. Эпюра крутящих моментов для данного вала также построена в долях параметра М. Известно: d=20мм, 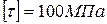
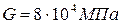
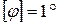
1. Чему равно касательное напряжение на участке (2-3) в долях параметра М?
1.
2.
3.
4.
2. Чему равно максимальное по абсолютной величине напряжение вала в долях параметра М?
1.
2.
3.
4.
3. Какое сечение или участок вала является наиболее опасным?
2. Сечение (1) участка (1-2)
3. Сечение (2) участка (1-2)
4. Чему равна величина максимально допустимого параметра М, найденного из условия прочности?
1.
2.
3.
4.
5. Чему равен абсолютный угол закручивания участка (0-1), если 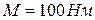
1.
2.
3.
4.
6. Чему равен угол закручивания сечения (2) относительно жесткой заделки, если 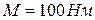
1.
2.
3.
4.
7. Чему равен максимальный по абсолютной величине угол закручивания вала относительно жесткой заделки (при 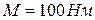
1.
2.
3.
4.
8. Выполняется ли условие жесткости по абсолютному углу закручивания?
2. Не выполняется
Вариант 2
Вал постоянного круглого поперечного сечения, изготовленный из малоуглеродистой стали Ст3, нагружен системой внешних самоуравновешенных крутящих моментов. Эпюра внутренних крутящих моментов 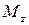
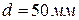
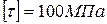
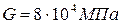

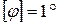
1. Чему равен полярный момент сопротивления круглого сечения вала?
1.
2.
3.
4.
2. Чему равно касательное напряжение в сечении (0)?
1.
2.
3.
4.
3. Чему равно касательное напряжение на участке (1-2)?
1.
2.
3.
4.
4. Чему равно максимальное по абсолютной величине напряжение вала?
1.
2.
3.
4.
5. Выполняется ли условие прочности?
2. Не выполняется
6. Чему равен абсолютный угол закручивания участка (0-1)?
1.
2.
3.
4.
7. Чему равен максимальный по абсолютной величине угол закручивания относительно сечения (0)?
1.
2.
3.
4.
8. Выполняется ли условие жесткости по абсолютному углу закручивания?
2. Не выполняется
Приложение 3. Ответы к тестам
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Сопротивление материалов (стр. 14 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
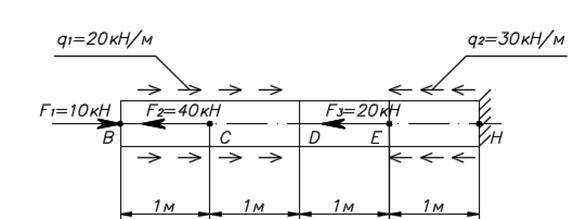
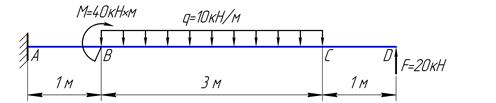
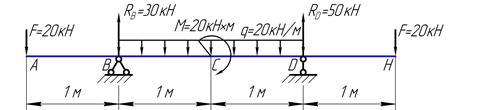
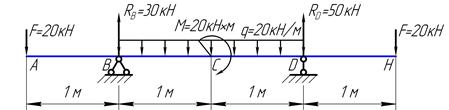
По часовой стрелке относительно точки А поворачивают балку распределенные силы q1 и q2:
Найдем моменты этих сил относительно точки А, применяя правило №3 (см. выше):
Против часовой стрелки относительно точки А поворачивают балку следующие усилия: сосредоточенный момент М, реактивная сила RB и сосредоточенная сила F.
Найдем моменты этих усилий относительно точки А, применяя правила №1 и №2 (см. выше):



Реакция RA относительно точки А момента не создает, потому что её линия действия проходит через эту точку и, соответственно, плечо её относительно точки А равно нулю:
Приравняем сумму моментов, поворачивающих балку относительно точки А по часовой стрелке, к сумме моментов, поворачивающих её относительно этой точки против часовой стрелки:
Подставив сюда найденные значения данных моментов, приходим к уравнению относительно неизвестной реакции RB:
Выразим из этого уравнения реакцию RB и найдем её численное значение, подставив известные значения внешних усилий и параметра а:
Значение реакции RB получилось положительное, значит мы угадали истинное её направление. Если знак реактивного усилия получается отрицательным, то его первоначально выбранное направление нужно изменить на противоположное.
4. Поступая аналогично, составим второе моментное уравнение равновесия: 
Мысленно открепив балку теперь от опоры А, получим рычаг с центром в точке В:
По часовой стрелке относительно точки В поворачивают балку следующие усилия: распределенная нагрузка q1, сосредоточенная сила F и реактивная сила RA.
Найдем моменты этих сил относительно точки В, применяя правила №2 и №3 (см. выше):
Против часовой стрелки относительно точки В поворачивают балку следующие усилия: распределенная нагрузка q2 и сосредоточенный момент М.
Найдем моменты этих усилий относительно точки В, применяя правила №1 и №3 (см. выше):
Реакция RВ относительно точки В момента не создает, потому что её линия действия проходит через точку В и, соответственно, плечо её относительно точки В равно нулю:
Приравняем сумму моментов, поворачивающих балку относительно точки В по часовой стрелке, к сумме моментов, поворачивающих её относительно этой точки против часовой стрелки:
Подставив сюда найденные значения данных моментов, приходим к уравнению относительно неизвестной реакции RА:
Выразим из этого уравнения реакцию RА и найдем её численное значение, подставив известные значения внешних усилий и параметра а:
Значение реакции RА также получилось положительное, значит мы угадали и её истинное направление.
5. Проверим правильность найденных значений реактивных усилий силовым уравнением равновесия в проекции на вертикальную ось Y: 


Подставим значения сил в уравнение:
Уравнение тождественно выполняется, значит реакции найдены верно.
Таким образом, реактивные силы нашей балки направлены вверх и равны, соответственно:


Задача решена
Приложение 2. Тестовый материал
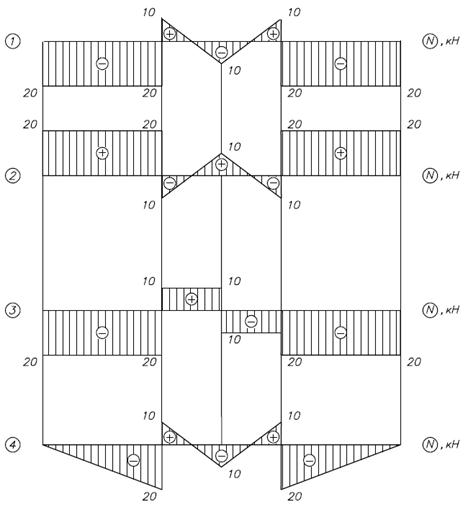
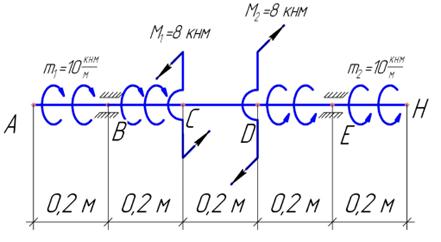
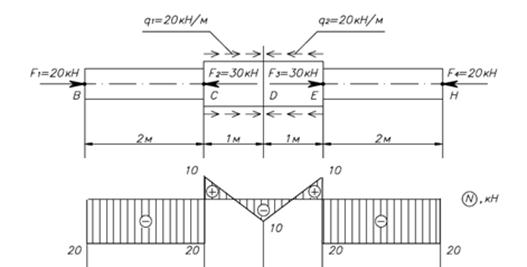
Тесты к теме 1.1 «Построение эпюры продольной силы»
1. На какое количество участков надо поделить данный стержень для построения эпюры N?
2. В каких сечениях данного стержня на эпюре N будут скачки?
1. В сечениях, где приложены сосредоточенные силы
2. В сечениях, где меняется размер сечения
3. В сечениях, где начинается и кончается распределенная нагрузка
4. В сечениях, где приложены сосредоточенные силы и где начинается и кончается распределенная нагрузка
3. На каких участках эпюры N для данного стержня будут прямые параллельные базе эпюры?
1. На участках ВС и ЕН
2. На участках CD и DE
4. На участках DE и EH
5. На всех участках
4. На каких участках эпюры N для данного стержня будут наклонные прямые?
1. На всех участках
2. Таких участков нет
3. На участках CD и DE
4. На участках ВС и СВ
5. На участках DE и EH
5. Выберите правильную эпюру N для данного стержня.
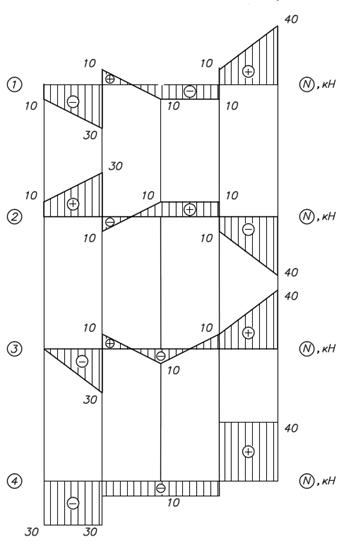
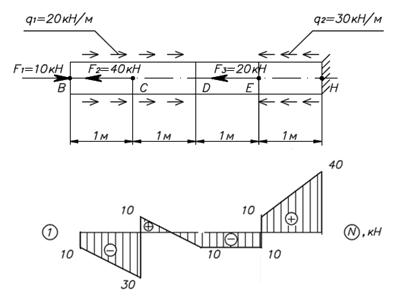
1. На какое количество участков надо поделить данный стержень для построения эпюры N?
2. В каких сечениях данного стержня на эпюре N будут скачки?
4. Во всех сечениях стержня
3. На каких участках эпюры N для данного стержня будут прямые параллельные базе эпюры?
1. На всех участках
2. На участках ВС и ЕН
3. На участках CD и DE
4. На каких участках эпюры N для данного стержня будут наклонные прямые?
1. На всех участках
2. На участках ВС и ЕН
3. На участках CD и DE
5. На участках DE и EH
5. Для данного стержня выберите правильную эпюру N.
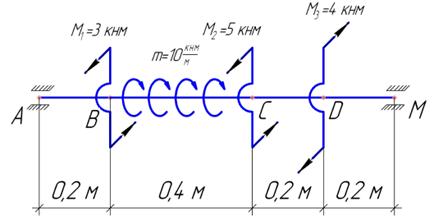
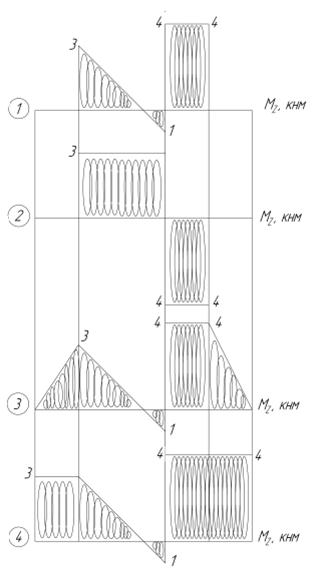
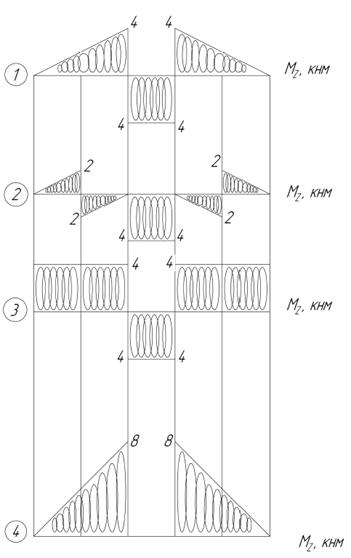
Тесты к теме 1.2 «Построение эпюры внутреннего крутящего момента»
1. На какое количество участков надо поделить данный вал для построения эпюры Мz?
Видео:Сопромат. Практическое занятие №1.4Скачать

Эпюры продольных усилий
Брус, работающий преимущественно на растяжение-сжатие называетсястержнем.
Правило знаков. Продольная сила N считается положительной, если
вызывает растяжение, и отрицательной, если вызывает сжатие.
Разбиваем стержень на участки, используя правила:
1) движемся со свободного конца;
2) границами участков являются сечения, в которых приложены внешние силы.
Рациональнее отбрасывать верхнюю часть, тогда нет необходимости определять реакцию опоры.
Проводим произвольное сечение 1-1 на 1-м участке (рис.3, б) и
рассматриваем равновесие нижней отсеченной части;
Искомые продольные усилия Ni всегда направляем на растяжение, т. е. в положительную сторону. Для определения продольных усилий нет необходимости каждый раз изображать отсеченную часть и записывать уравнение равновесия. Можно сразу записывать выражение для продольного усилия, как алгебраическую сумму проекций на ось бруса внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Знак минус указывает, что фактическое направление силы N2 противоположно первоначально выбранному, т.е. 2-й участок испытывает сжатие.
3-й участок (рис. 3, г): N3 = F1 — F2 + F3 = F- 2F + 4F = ЗF, По полученным значениям строим эпюру, показанную на рис. 3, д. Положительные значения откладываем вправо, а отрицательные – влево от оси.
Правило: В местах приложения сосредоточенных сил на эпюре получаются «скачки». Размер «скачка» равен приложенной в этом сечении силе. Направление «скачка» связано с направлением действия силы.
Замечание. Скачкообразные изменения координат N носят условный характер, так как условно и само понятие «сосредоточенная сила». Фактическая внешняя сила распределена по некоторой небольшой части длины бруса; в пределах этой части значения N изменяется по некоторому закону, установить который не предоставляется возможным. Не известный криволинейный переходный участок эпюры заменяют условным «скачком». На вопрос: чему равна продольная сила в точке приложения F2 , ответить прямо нельзя. Можно лишь сказать, что бесконечно близко к точке справа N = + F, а бесконечно близко к точке сверху N = — F.
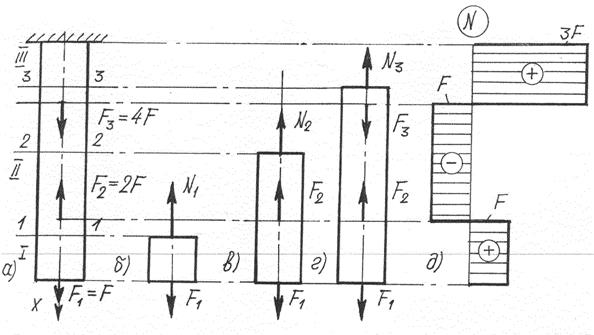
Участки остаются те же, но должна быть задана, длинна участков. 1 участок: 0 ≤ x1 ≤ 0,5а:
Это уравнение прямой линии, поэтому для построения эпюры достаточно определить значение N в начале и в конце участка:
Правило: На участке, где действует распределенная нагрузка, на эпюре – наклонная прямая.
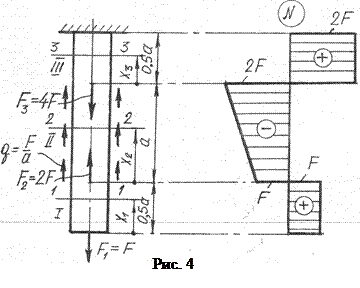
4. Эпюры крутящих моментов
Брус, работающий преимущественно на кручение, называется валом.
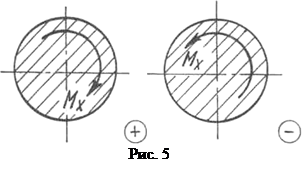
Правило знаков. Знак крутящего момента не имеет физического смысла, но для определенности при построении эпюр условимся о следующем правиле знаков.
Будем считать крутящий момент положительным, если при взгляде со стороны сечения, он представляется направленным по часовой стрелке (рис. 5).
Момент Мо не задан, его можно определить из уравнения равновесия ΣМх = 0, но рациональнее вести построение эпюры, двигаясь со свободных концов слева, а затем справа. Величину Мо можно будет определить по построенной эпюре без вычислений. Разбиваем вал на 3 участка. Используем метод сечений, рассматривая равновесие оставленной части (рис. 6, б, в, г), приходим к выводу, что внутренние силы, возникающие в поперечном сечении вала, должны дать крутящий момент, уравновешивающий внешние моменты, приложенные к оставленной части.
Проводим произвольные сечения на каждом из 3-х участков и рассматривая равновесие отсеченных частей, получим:
По полученным значениям строим эпюру, представленную на рис. 6, д.
5. Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом. Особенности эпюр поперечных сил и изгибающих моментов
Построение эпюр Q и Мизг существенно упрощается при использовании дифференциальных зависимостей между q, Q, Мизг. Для вывода этих зависимостей выделим из балки двумя поперечными сечениями, расстояние между которыми равно dх, бесконечно малый элемент (рис. 7).
Распределенную нагрузку q направляем вверх, так как это направление считаем положительным.
В общем случае q может быть не равномерной, но из-за малости dх неравномерность не учитывается.
Спроецируем действующие на элемент силы на ось Оу:
Производная от поперечной силы по длине балки ровна интенсивности распределенной нагрузки.
Определим сумму моментов относительно точки К;
ΣМк= 0: Мz + Qуdх + qdx dx/2 — (Мz + dМz) = 0 , пренебрегая малыми второго порядка, получим:
Производная от изгибающего момента по длине балки равна поперечной силе.
Из этих зависимостей следует:
Интенсивность распределенной нагрузки равна второй производной от изгибающего момента по длине балки.
В сложных случаях нагружения балок эпюры Q и Мизг целесообразнее строить без записи аналитических выражений Q(х), Мизг(х) по участкам, вычисляя значения Q, Мизг только в характерных точках — это границы участков и лишь в отдельных случаях — промежуточные сечения. При таком построении используется ряд правил, которые являются следствием из полученных дифференциальных зависимостей:
1. На участках, где нет распределенной нагрузки q:
— эпюра Q — прямая, параллельная базе, т.е. Q = сonst,
— эпюра Мизг — наклонная прямая (рис. 8).
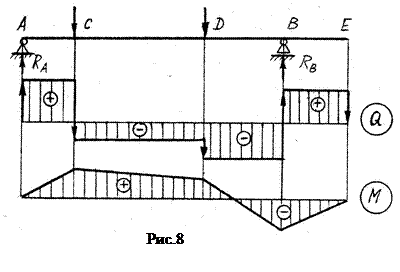
2. На участках, где приложена равномерно распределенная нагрузка q:
— эпюра Q — наклонная прямая,
— эпюра Мизг — парабола (кривая второго порядка) с выпуклостью, направленной против направления q (рис. 9).
📺 Видео
Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

ПЗ Часть 3 Эпюра крутящего моментаСкачать

БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Понимание напряжений в балкахСкачать

11. Кручение ( практический курс по сопромату )Скачать

Правило знаков при крученииСкачать

Построение эпюр поперечных сил и изгибающих моментов в балке.Скачать

Крутящий момент. ВведениеСкачать

РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать

12. Подбор сечения при кручении ( практический курс по сопромату )Скачать

Вот для чего нужно строить эпюры в сопромате!Скачать

Пример построения эпюры крутящего момета ЭТСкачать

Расчет значений Q и M для построения эпюр поперечных сил и изгибающих моментов балки на двух опорахСкачать

Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

Построение эпюры крутящих моментовСкачать

18. Подбор сечения при изгибе и кручении ( практический курс по сопромату )Скачать

РАМА. ПОСТРОЕНИЕ ЭПЮР Q, M, N. Сопромат.Скачать

Построение эпюр в балке ( Q и M ). СопроматСкачать