Тест на тему окружность 8 класс ответы (4 видео)

Тест по геометрии по теме «Окружности» ( 8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Содержание

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Тест по теме «Окружность» тест по геометрии (8 класс) по теме
Скачать:
Предварительный просмотр:
Тест по теме: «Окружность» геометрия 8 класс
Просмотр содержимого документа «Тест по теме: «Окружность» геометрия 8 класс»
🔍 Видео

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 376 МОСКОВСКОГО РАЙОНА САНКТ-ПЕТЕРБУРГА

ТЕСТ ПО ГЕОМЕТРИИ

по теме «Окружности»

для учащихся 8 класса

Осипова Алла Владимировна

Осипова Алла Владимировна

Государственное бюджетное общеобразовательное учреждение

Средняя общеобразовательная школа № 376 Московского района Санкт-Петербурга

Тест по геометрии «Окружности».

Комплектация работы. Работа состоит из одного данного файла.

Тест по геометрии «Окружности» предназначен для учащихся 8-9 классов общеобразовательных школ. Он может быть использован как для тематического контроля знаний по итогам изучения темы «Окружности» в 8 классе, так и в процессе подготовки к Государственной итоговой аттестации в 9 классе. Тест может быть использован и в 11 классе при повторении планиметрии и подготовке к сдаче ЕГЭ.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Тесты по геометрии для 8 класса по теме: «Окружности» составлены на основе примерной программы основного общего образования по математике в соответствии с федеральным компонентом государственного стандарта и с учетом рекомендаций авторских программы Л.С.Атанасяна, c огласно базисному учебному плану средней школы, рекомендациям Министерства образования Российской Федерации.

Материал, содержащийся в данном тесте, позволяет помочь учащимся научиться уверенно выполнять задания как стандартные, так и нестандартные. Содержит задачи на повторение всех теорем о вписанных и центральных углах, об углах, образованных хордами, касательными и секущими.

Необходимость данного теста обуславливается также и тем, что задания, связанные со свойствами окружностей, встречаются в материалах ГИА и ЕГЭ.

Тест предназначен как для учащихся, проявляющих интерес к математике , так и для желающих проверить уровень своих знаний по указанной теме.

Тест состоит из 24 заданий, представлен в четырех вариантах. По трудности варианты между собой равноценны. Каждое задание теста имеет 5 вариантов ответа, из которых только один является верным.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тест по теме «Окружность»
тест по геометрии (8 класс) по теме

Данный тест составлен по теме «Окружность» и предназначен для учащихся 8 класса. Представленные задания позволяют своевременно выявить затруднения учащихся и предупредить устойчивые пробелы в их знаниях, их можно использовать при организации обобщающего повторения по указанной теме и для подготовки к итоговой аттестации.

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Скачать:

Вложение	Размер
test_okruzhnost2.doc	123 КБ

Видео:Геометрия 8 класс. Касательная к окружностиСкачать

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

«Альшеевская средняя общеобразовательная школа Буинского

муниципального района Республики Татарстан»

Разработка теста по теме

для учащихся 8 класса

Автор разработки:
учитель математики
Афанасьева Валентина Николаевна

Фамилия имя отчество: Афанасьева Валентина Николаевна

Место работы, район, занимаемая должность: Муниципальное бюджетное общеобразовательное учреждение «Альшеевская средняя общеобразовательная школа Буинского муниципального района Республики Татарстан»,Буинский, учитель математики

Работа состоит из данного документа.

Материал, содержащийся в данном тесте, позволяет помочь учащимся научиться уверенно решать как стандартные, так и нестандартные задачи. Необходимость данного теста обуславливается так же и тем, что задания встречаются в материалах ГИА.

Тест предназначен как для учащихся, проявляющих интерес к изучению математики, так и для учащихся, желающих повысить свой уровень математической подготовки.

Тест состоит из 20 заданий по 4 варианта трех уровней сложности. По трудности варианты между собой равноценны. Каждое задание теста имеет 5 вариантов ответа, из которых только один является верным.

Касательная к окружности

Центральные и вписанные углы

Четыре замечательные точки окружности

Вписанные и описанные окружности

Тест по теме «Окружность»

1) А) AB и BC – отрезки касательных, проведенных из точки В к окружности с

центром О. ОА= 16 см, а радиусы, проведенные к точкам касания,

разуют угол, равный 120˚. Чему равен отрезок ОВ?

а) 32 см б) 16 см в) 8 см г) 24 см д)48 см.

Б) AB и АC – отрезки касательных, проведенных из точки А к окружности

центром О. ОС= 18 см, а радиусы, проведенные к точкам касания,

образуют угол, равный 120˚. Чему равен отрезок ОА?

а )18 см б) 36 см в)9 см г)28 см д)42 см

В) Отрезки касательных АВ и ВС, проведенных из точки В к окружности с

центром О, образуют угол, равный 60˚, ОВ = 28 см. Чему равен отрезок

а) 42 см б)56 см в) 14 см г)28 см д)7см

Г) Отрезки касательных АВ и АС, проведенных из точки А к окружности с

центром О, образуют угол, равный 60˚, ОВ = 15 см. Чему равен отрезок ОА?

а)40 см б)7,5 см в) 45 см г) 30 см д) 60 см

2) А) Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенных из точки А. Найдите угол ВАС, если ОА=30 см, ОВ= 15 см.

а) 30˚ б) 60˚ в) 120˚ г) 150˚ д) 180˚

Б) Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенных из точки А. Найдите угол ВОС, если ОА=30 см, ОВ= 15 см.

а) 30˚ б) 60˚ в) 120˚ г) 150˚ д) 180˚

В) Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенных из точки А. Найдите угол ВОС, если ОА=32 см, ОС= 16 см.

а) 30˚ б) 60˚ в) 120˚ г) 150˚ д) 180˚

Г) Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенных из точки А. Найдите угол ВАС, если ОА=34 см, ОВ= 17 см.

а) 30˚ б) 60˚ в) 120˚ г) 150˚ д) 180˚

3) А) Прямая АВ касается окружности с центром О радиуса 2 см в точке А так, что ОА = АВ. Чему равен отрезок ОВ?

а) 4 см б) 2 см в) 3√2 см г) 2√2 см д) 4 √2 см

Б) Прямая АВ касается окружности с центром О радиуса 3 см в точке В так, что ОВ = АВ. Чему равен отрезок ОА?

а) 4 см б) 2 см в) 3√2 см г) 2√2 см д) 4 √2 см

В) Прямая АВ касается окружности с центром О радиуса 4 см в точке А так, что ОВ = 4√2 см . Чему равен отрезок АВ?

а) 4 см б) 2 см в) 3√2 см г) 2√2 см д) 4 √2 см

Г) Прямая АВ касается окружности с центром О радиуса 5 см в точке В так, что ОА =5 √2 см . Чему равен отрезок АВ?

а) 4 см б) 5 см в) 3√2 см г) 2√2 см д) 4 √2 см

4) А) Прямая АВ касается окружности с центром О радиуса 6 см. Известно, что АВ = 16 см, АО = ОВ. Чему равна длина АО?

а) 8 см б) 10 см в) 6 см г) 9 см д) 16 см

Б) Прямая АВ касается окружности с центром О радиуса 5 см. Известно, что АО = ОВ = 13 см. Чему равна длина АВ?

а) 26 см б) 24 см в) 10см г) 12 см д) 16 см

В) Прямая АВ касается окружности с центром О радиуса 3 см. Известно, что АВ = 8 см, АО = ОВ. Чему равна длина ВО?

а) 8 см б) 10 см в) 6 см г) 9 см д) 5 см

Г ) Прямая АВ касается окружности с центром О радиуса 7 см. Известно, что АО = ОВ = 25 см. Чему равна длина АВ?

а)4 8 см б) 50 см в) 60см г) 90 см д) 14 см

5 ) А) Стороны АВ , ВС и АС треугольника касаются окружности с центром О в точках М, К, и P соответственно так, что ВМ = 4 см, КС = 6 см, AP = 8 см. Найдите периметр треугольника.

а)4 8 см б) 36 см в) 28см г) 72 см д) 18 см

Б) Стороны АВ , ВС и АС треугольника касаются окружности с центром О в точках М, К, и P соответственно так, что ВМ = 5 см, PС = 7см, а периметр треугольника АВС равен 32 см. Найдите длину стороны АС.

а)16 см б) 15 см в) 11см г) 12 см д) 14 см

В) Стороны АВ , ВС и АС треугольника касаются окружности с центром О в точках М, К, и P соответственно так, что ВМ = 3 см, КС = 4 см, AP = 5см. Найдите периметр треугольника.

а) 8 см б) 12 см в) 60см г) 25 см д) 24 см

Г) Стороны АВ , ВС и АС треугольника касаются окружности с центром О в точках М, К, и P соответственно так, что КВ = 5 см, СP = 8 см, а периметр треугольника АВС равен 48 см. Найдите длину стороны АВ.

а) 16 см б) 19 см в) 13см г) 26 см д) 36 см

6) А) Вершины треугольника АВС лежат на окружности, угол А = 70˚, угол С = 30˚ .Чему равна градусная мера дуги АС ?

а) 100˚ б) 60˚ в) 120˚ г) 140˚ д) 160˚

Б) Вершины треугольника АВС лежат на окружности, угол А = 50˚, угол В = 45˚ .Чему равна градусная мера дуги АВ ?

а) 95˚ б) 100˚ в) 170˚ г) 140˚ д) 160˚

В) Вершины треугольника АВС лежат на окружности, угол В = 60˚, угол С = 30˚ .Чему равна градусная мера дуги ВС ?

а) 100˚ б) 90˚ в) 120˚ г) 180˚ д) 60˚

Г) Вершины треугольника АВС лежат на окружности, угол А = 40˚, угол С = 80˚ .Чему равна градусная мера дуги АС ?

а) 100˚ б) 60˚ в) 120˚ г) 140˚ д) 160˚

7) А) Точки АВС лежат на окружности с центром в точке О.ᴗВС:ᴗАС =3:4, угол ВСА = 40˚. Чему равен угол ВОС?

а) 100˚ б) 60˚ в) 120˚ г) 140˚ д) 160˚

Б) Точки АВС лежат на окружности с центром в точке О.ᴗАВ:ᴗАС =2:3, угол ВАС = 55˚. Чему равен угол АОС?

а) 110˚ б) 150˚ в) 120˚ г) 100˚ д) 75˚

В) Точки АВС лежат на окружности с центром в точке О.ᴗАС:ᴗАВ =4:5, угол ВАС = 45˚. Чему равен угол АОС?

а) 120˚ б) 60˚ в) 100˚ г) 140˚ д) 160˚

Г) Точки АВС лежат на окружности с центром в точке О.ᴗАВ:ᴗВС =3:5, угол АВС = 60˚. Чему равен угол АОВ?

а) 100˚ б) 80˚ в) 120˚ г) 90˚ д) 60˚

8) А) Хорды АВ и СD пересекаются в точке Е, АЕ = 4 см, ВЕ = 9 см, СЕ = 12 см. Найдите длину DЕ.

а)27 см б) 3 см в) 28см г) 7 см д) 16 см

Б) Хорды АВ и СD пересекаются в точке К, АК = 6 см, ВК = 8 см, СК = 4 см. Найдите длину DК.

а)3 см б) 5,3 см в) 6см г) 12 см д) 18 см

В) Хорды АВ и СD пересекаются в точке О, АО = 7 см, ВО = 4 см, СО = 14 см. Найдите длину DО.

а) 2см б) 4 см в) 25см г) 18 см д) 8 см

Г) Хорды АВ и СD пересекаются в точке М, АМ = 8 см, ВМ = 4 см, СМ = 2 см. Найдите длину DМ.

. а)5 см б) 14 см в) 16см г) 12 см д) 8 см

9) А) Через точку А проведены касательная АВ (В – точка касания) и секущая, пересекающая окружность в точках С и Е так, что АВ = 10 см, АЕ = 20 см. Найдите длину АС.

а)5 см б) 14 см в) 16см г) 12 см д) 8 см

Б) Через точку А проведены касательная АВ (В – точка касания) и секущая, пересекающая окружность в точках С и К так, что АC = 4 см, АК = 16 см. Найдите длину АВ.

а)10 см б) 14 см в) 16см г) 12 см д) 8 см

В) Через точку А проведены касательная АВ (В – точка касания) и секущая, пересекающая окружность в точках С и D так, что АВ = 4 см, АC = 2 см. Найдите длину СD.

а)6 см б) 14 см в) 16см г) 12 см д) 8 см

Г) Через точку А проведены касательная АВ (В – точка касания) и секущая, пересекающая окружность в точках С и O так, что АВ = 8 см, АO = 16 см. Найдите длину АС.

а)5 см б) 14 см в) 4см г) 12 см д) 8 см

10) А) точки А,В,С и К лежат на окружности так, что АК – диаметр, угол САК равен 20˚, угол ВСА = 40˚.Найдите величину угла АВС.

а) 110˚ б) 80˚ в) 120˚ г) 90˚ д) 60˚

Б) Точки А,В,С и Е лежат на окружности так, что АЕ – диаметр, угол ВАС равен 50˚, угол ВЕА = 10˚.Найдите величину угла САЕ.

а) 100˚ б) 30˚ в) 120˚ г) 90˚ д) 60˚

В) Точки А,В,С и D лежат на окружности так, что АD – диаметр, угол САD равен 30˚, угол ВСА = 40˚.Найдите величину угла АВС.

а) 100˚ б) 80˚ в) 120˚ г) 90˚ д) 60˚

Г) Точки А,В,С и F лежат на окружности так, что АF – диаметр, угол BАC равен 60˚, угол ВFА = 20˚.Найдите величину угла АВС.

а) 100˚ б) 80˚ в) 120˚ г) 90˚ д) 60˚

11) А) Хорды АВ и CD пересекаются в точке Е. Найдите длину АВ, если СЕ = 8 см, DЕ = 9 см, а длина АЕ в два раза больше длины ВЕ.

а)6 см б) 17 см в) 36см г) 12 см д) 18 см

Б) Хорды АВ и CD пересекаются в точке М. Найдите длину АВ, если СМ = 4 см, DМ = 12 см, а длина АМ в три раза больше длины ВМ.

а)6 см б) 14 см в) 16см г) 12 см д) 8 см

В) Хорды АВ и CD пересекаются в точке К. Найдите длину CD, если АK = 4 см, BK = 15 см, а длина СК на 7 см меньше длины DK.

а)6 см б) 14 см в) 16см г) 17 см д) 8 см

Г) Хорды АВ и CD пересекаются в точке Х. Найдите длину CD, если АX =6 см, ВX = 5 см, а длина СX на 1 см меньше длины DХ.

а)6 см б) 14 см в) 11см г) 12 см д) 8 см

12) А) В треугольнике АВС серединные перпендикуляры к сторонам АВ и ВС пересекаются в точке О, ВО = 10 см, угол АСО = 30˚. Найдите расстояние от точки О до стороны АС.

а)5 см б) 10 см в) 15см г) 20 см д) 8 см

Б) В треугольнике АВС серединные перпендикуляры к сторонам АВ и ВС пересекаются в точке О, АО = 12 см, угол ВСО = 30˚. Найдите расстояние от точки О до стороны BC.

а)15 см б) 10 см в) 6см г) 20 см д) 8 см

В) В треугольнике АВС серединные перпендикуляры к сторонам АВ и ВС пересекаются в точке О, СО = 16 см, угол АВО = 30˚. Найдите расстояние от точки О до стороны АB.

а)5 см б) 10 см в) 15см г) 12 см д) 8 см

Г) В треугольнике АВС серединные перпендикуляры к сторонам АВ и ВС пересекаются в точке О, ВО = 14 см, угол САО = 30˚. Найдите расстояние от точки О до стороны АС.

а)5 см б) 10 см в) 15см г) 7 см д) 8 см

13) А) В треугольнике АВС высоты АК и ВЕ пересекаются в точке О, угол САВ = 42˚. Чему равен угол АВЕ?

а) 48˚ б) 138˚ в) 42˚ г) 132˚ д) 60˚

Б) В треугольнике АВС высоты АК и СЕ пересекаются в точке О, угол СAB= 53˚. Чему равен угол AСЕ?

а) 106˚ б) 37˚ в) 53˚ г) 90˚ д) 60˚

В) В треугольнике АВС высоты АP и CK пересекаются в точке О, угол САВ = 56˚. Чему равен угол ACK?

а) 156˚ б) 34˚ в) 112˚ г) 90˚ д)1 60˚

Г) В треугольнике АВС высоты АP и CK пересекаются в точке О, угол САВ = 64˚. Чему равен угол ACK?

а) 128˚ б) 34˚ в) 32˚ г) 26˚ д) 64˚.

14) А) В равнобедренном треугольнике АВС, АВ = ВС, медианы АЕ и СК пересекаются в точке М, ВМ = 6 см, АС = 10 см. Чему равна площадь треугольника АВС?

а) 120 см² б) 60 см² в) 90 см² г) 45 см² д) 64 см².

Б) В равнобедренном треугольнике АВС, АВ = AС, медианы BK и СP пересекаются в точке М, AМ = 4 см, BС = 9 см. Чему равна площадь треугольника АВС?

а) 36 см² б) 27 см² в) 72 см² г) 45 см² д) 54 см².

В) В равнобедренном треугольнике АВС, АС = ВС, медианы АЕ и ВК пересекаются в точке М, СМ = 2 см, АВ = 12 см. Чему равна площадь треугольника АВС?

а) 18 см² б) 6 см² в) 9 см² г) 24 см² д) 48 см².

Г) В равнобедренном треугольнике АВС, АС = ВС, медианы АЕ и ВК пересекаются в точке М, СМ = 8 см, АB = 5 см. Чему равна площадь треугольника АВС?

а) 120 см² б) 60 см² в) 90 см² г) 30 см² д) 40 см²

15) А) В треугольнике АВС угол В – прямой, АС = 10 см, ВС = 8 см, К – середина стороны АС. Из точки К опущен перпендикуляр КЕ к стороне ВС. Найдите длину КЕ.

а)6 см б) 3 см в) 1см г) 4 см д) 5 см

Б) В треугольнике АВС угол В – прямой, АС = 5 см, ВС = 4 см, К – середина стороны АС. Из точки К опущен перпендикуляр КЕ к стороне ВС. Найдите длину КЕ.

а)3 см б) 6,6 см в) 1,5см г) 1,6 см д) 8,6 см

В) В треугольнике АВС угол В – прямой, АС = 10 см, ВС = 8 см, К – середина стороны АС. Из точки К опущен перпендикуляр КЕ к стороне АВ. Найдите длину КЕ.

а)6 см б) 4 см в) 3см г) 5 см д) 8 см

Г) В треугольнике АВС угол В – прямой, АС = 13 см, ВС = 12 см, К – середина стороны АС. Из точки К опущен перпендикуляр КЕ к стороне АВ. Найдите длину КЕ.

а)6 см б) 6,6 см в) 1,6см г) 16,6 см д) 8,6 см

16) А) В треугольнике АВС высоты ААˡи ССˡˌпересекаются в точке Н. Найдите высоту, проведенную к стороне АС, если HAˡ = 6 см, ВАˡ = 8 см, АН= 11 см.

а)6 см б) 6,6 см в) 1,6см г) 16,6 см д) 8,6 см

Б) В треугольнике АВС высоты ААˡи ССˡ пересекаются в точке Н. Найдите высоту, проведенную к стороне АС, если HAˡ = 3 см, ВАˡ = 4 см, АН= 4 см.

а)6,6 см б) 1,4 см в) 2,4 см г) 7,4 см д) 8 см

В) В треугольнике АВС высоты ААˡи ССˡ пересекаются в точке Н. Найдите высоту, проведенную к стороне АС, если HAˡ = 9 см, ВАˡ = 12 см, АН= 11 см.

а)60 см б) 21,6 см в) 10,8 см г) 20 см д) 8,5 см

Г) В треугольнике АВС высоты ААˡи ССˡ пересекаются в точке Н. Найдите высоту, проведенную к стороне АС, если HAˡ = 5 см, ВАˡ = 12 см, АН= 26 см.

а)62 см б) 17 см в) 23см г) 12 см д)3 8 см.

17) А) В равносторонний треугольник вписана окружность радиуса 4см. Чему равна сторона треугольника?

а) 2√2 см б) 4√3 см в) 6√3см г) 8√3 см д) 8√2 см.

Б) В равносторонний треугольник вписана окружность радиуса 3 см. Чему равна сторона треугольника?

а)2√2 см б) 6√3 см в) 2√5см г) 4 √3см д) 4√5 см.

В) В равносторонний треугольник вписана окружность радиуса 6 см. Чему равна сторона треугольника?

а)6 см б) 6 √2см в) 6√3см г) 12√3 см д)3√3 см.

Г) В равносторонний треугольник вписана окружность радиуса 8 см. Чему равна сторона треугольника?

а)6√3 см б) 16√3 см в) 26√2см г) 12√3 см д) 8√3 см.

18) А) Четырехугольник АВСD описан около окружности. АВ = 7 см, CD =11 см, ВС в два раза меньше AD. Найдите длину ВС.

а)22 см б) 14 см в) 6 см г) 7 см д) 8 см

Б) Четырехугольник АВСD описан около окружности. ВС = 6 см, АD =9 см, АВ в два раза больше СD. Найдите длину АВ.

а)5 см б) 10 см в) 15см г) 7 см д) 8 см

В) Четырехугольник АВСD описан около окружности. АВ = 4 см, СD =5 см, ВС в два раза меньше AD. Найдите длину ВС

а)5 см б) 10 см в) 3см г) 7 см д) 8 см

Г) Четырехугольник АВСD описан около окружности. ВС = 7 см, АD =8 см, АВ в два раза больше СD. Найдите длину АВ.

а)5 см б) 10 см в) 15см г) 7 см д) 8 см

19) А) Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см. Найдите площадь этого треугольника.

а) 120 см² б) 126 см² в) 128 см² г)130 см² д)140 см²

Б) Равнобедренный треугольник с основанием 8 см, вписан в окружность радиуса 5 см. Найдите площадь этого треугольника.

а) 32 см² б) 60 см² в) 90 см² г) 30 см² д) 40 см²

В) Равнобедренный треугольник с высотой, проведенной к основанию и равной 8 см, вписан в окружность радиуса 5 см. Найдите площадь этого треугольника.

а) 12 см² б) 62 см² в) 92 см² г) 32 см² д) 40 см²

Г) Равнобедренный треугольник с основанием 6 см, вписан в окружность радиуса 5 см. Найдите площадь этого треугольника.

а) 12 см² б) 6 см² в) 9 см² г) 27 см² д) 18 см²

20) А) В прямоугольном треугольнике АВС ( угол С = 90˚) АС+ ВС = 17 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.

а) 120 см² б) 60 см² в) 90 см² г) 30 см² д) 40 см²

Б) В прямоугольном треугольнике АВС ( угол С = 90˚) АВ = 10 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.

а) 120 см² б) 60 см² в) 90 см² г) 30 см² д) 24 см²

В) В прямоугольном треугольнике АВС ( угол С = 90˚) АВ = 5 см, радиус вписанной в него окружности равен 1 см. Найдите площадь этого треугольника.

а) 6 см² б) 12 см² в) 24 см² г) 30 см² д) 40 см²

Г) В прямоугольном треугольнике АВС ( угол С = 90˚) АС+ ВС = 14 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.

а) 120 см² б) 24 см² в) 12 см² г) 30 см² д) 40 см²

Видео:Ответы на вопросы к § 10 - Геометрия 8 класс МерзлякСкачать

Тест по теме: «Окружность» геометрия 8 класс

Тесты для проверки знаний по теме: Окружность. Два варианта по 10 вопросов.

Просмотр содержимого документа
«Тест по теме: «Окружность» геометрия 8 класс»

Тест по теме: «Окружность» 8 класс

1. Выбрать верные утверждения: а) угол с вершиной на окружности называется её центральным углом; б) центральный угол измеряется дугой , на которую он опирается; в) угол, образованный двумя хордами окружности, называется вписанным углом этой окружности; г) вписанный угол измеряется половиной дуги, на которую он опирается.

2. Могут ли быть перпендикулярными радиус и хорда, проведённые из одной и той же точки окружности? а) могут, б) не могут.

3. Даны квадрат ОАВС, сторона которого равна 5см, и окружность с центром в точке О радиуса 4см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности? а) ОА и АВ; б) ОА и ВС; в) ВС и АС; г) ОА и АС.

4. Через точку М окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними. а) 45°; б) 30°; в) 90°; г) 60°.

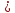
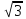
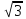
5. Прямая МN касается окружности c центром О радиуса r в точке N. Найдите MN. ЕслиМON =60° , а r = 12cм. а) 12; б) 12; 6; г) 24.

6. Найти вписанный угол АВС, если дуга АС, на которую он опирается, равна 58°. а) 116°; б) 29°; в) 90°; г) 58°.

7. Вписанный угол MNP опирается на дугу MN и равен 46°. Найти градусную меру дуги MN. а) 92°; б) 46°; в) 23°; г) 60°.

8. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 33°. Большая дуга окружности, заключённая между сторонами этого угла, равна 110°. Найти меньшую дугу. а) 22°; б) 11°; в) 44°; г) 33°.

9. Найти острый угол, образованный двумя секущими, проведёнными из точки , лежащей вне окружности, если дуги, заключённые между секущими, равны 130° и 42°. а) 42°; б)21°; в) 44°; г) 22°.

10. Указать верное утверждение а) не в каждый треугольник можно вписать окружность; б) в любой четырёхугольник можно вписать окружность; в) около любого треугольника можно описать окружность; г) если сумма противоположных углов четырёхугольника равна 360°, то около него можно описать окружность.

Тест по теме: «Окружность» 8 класс

1. Выбрать верные утверждения: а) угол с вершиной в центре окружности называется её центральным углом; б) центральный угол измеряется половиной дуги , на которую он опирается; в) угол, вершина, которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом этой окружности; г) вписанный угол измеряется дугой, на которую он опирается.

2.Из одной точки окружности проведены две хорды. Сколько получилось дуг? а) 2; б)4; в) 5; г) 3.

3. Даны квадрат ОАВС, сторона которого равна 7см, и окружность с центром в точке О радиуса 6см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности? а) ОА и АВ; б) ОА и ВС; в) ВС и АС; г) ОА и АС.

4. Через точку В окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними. а) 45°; б) 30°; в) 60°; г) 90°.

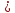
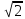
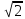
5. Прямая МN касается окружности c центром О радиуса r в точке N. Найдите MN. ЕслиМON = 45° , а r = 8cм. а) 8; б) 4; 4; г) 8.

6. Найти вписанный угол АВС, если дуга АС, на которую он опирается, равна 64°. а) 90°; б) 128°; в) 64°; г) 32°.

7. Вписанный угол MNP опирается на дугу MN и равен 52°. Найти градусную меру дуги MN. а) 208°; б) 52°; в) 26°; г) 104°.

8. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 44°. Большая дуга окружности, заключённая между сторонами этого угла, равна 100°. Найти меньшую дугу. а) 24°; б) 12°; в) 6°; г) 44°.

9. Найти острый угол, образованный двумя секущими, проведёнными из точки , лежащей вне окружности, если дуги, заключённые между секущими, равны 110° и 62°. а) 62°; б)24°; в) 48°; г) 22°.

10. Указать верное утверждение а) в каждый треугольник можно вписать окружность; б) в любой четырёхугольник можно вписать окружность; в) нельзя около любого треугольника описать окружность; г) если сумма противоположных углов четырёхугольника равна 360°, то около него можно описать окружность.