Теоремы о пропорциональных отрезках на параллельных прямых и отсекаемых параллельными прямыми

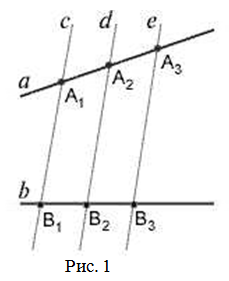
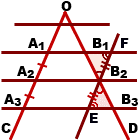
Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.

Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.

Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.

А можно и в такой:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.

Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А₁В₁ могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Для иллюстрации можно воспользоваться рисунком 1.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Как пользоваться теоремой Фалеса на практике

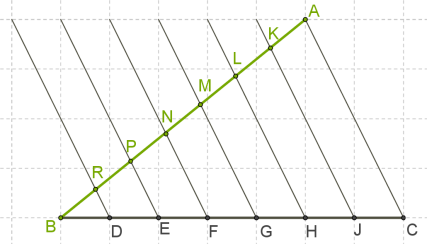
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.

Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Видео:Пропорциональные отрезки. Теорема о пропорциональных отрезкахСкачать

Обратная теорема Фалеса

Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:

Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.

Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.

Видео:Теорема о пропорциональных отрезкахСкачать

Доказательство теоремы Фалеса

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

Выберем точку В₂ и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А₁А₃ || EF. Рассматривая четырехугольник

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

Видео:Параллельность прямых. 10 класс.Скачать

Кто впервые доказал теорему о пропорциональных отрезках

По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.

Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.

Видео:Теорема фалеса. Теорема о пропорциональных отрезках - геометрия 8 классСкачать

Теорема Фалеса: формулировка и пример решения задачи

В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.

Видео:Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Формулировка теоремы

Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.

Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.

Обобщенная формулировка

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.

В соответствии с этим для нашего чертежа выше справедливо следующее равенство:

* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.

Обратная теорема Фалеса

1. Для пересекающихся секущих

Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.

Из обратной теоремы следует:

Обязательное условие: равные отрезки должны начинаться от вершины.

2. Для параллельных секущих

Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.

Видео:Параллельные прямые (задачи).Скачать

Пример задачи

Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.

Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.

Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).

Видео:Теорема Фалеса. 8 класс.Скачать

Реферат на тему «Теоремы о пропорциональных отрезках»

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Титульный лист

Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Введение

Великий учёный Фалес Милетский основал одну из прекраснейших наук – геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Является автором многих геометрических понятий и теорем, в том числе теоремы о пропорциональных отрезках.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Особое место в планиметрии отведено двум замечательным теоремам: теореме Чевы и теореме Менелая. Эти теоремы не включены в базовую программу курса геометрии средней школы, но их изучение (и применение) рекомендуется всем, кто интересуется математикой чуть больше, чем это возможно в рамках школьной программы. Чем же интересны эти теоремы? Сначала отметим, что при решении геометрических задач продуктивно сочетаются два подхода:

— один основан на определении базовой конструкции (например: треугольник – окружность; треугольник – секущая прямая; треугольник – три прямых, проходящих через его вершины и пересекающиеся в одной точке; четырехугольник с двумя параллельными сторонами и т.п.),

— а второй – метод опорных задач (простых геометрических задач, к которым сводится процесс решения сложной задачи).

Так вот, теоремы Менелая и Чевы относятся к наиболее часто встречающимся конструкциям: первая рассматривает треугольник, стороны или продолжения сторон которого пересечены некоторой прямой (секущей), во второй речь идет о треугольнике и трех прямых, проходящих через его вершины, пересекающиеся в одной точке.

Цель работы – изучить теоремы Фалеса, Чевы и Менелая и рассмотреть применение этих теорем к решению планиметрических задач.

Видео:Теорема о пропорциональных отрезкахСкачать

Глава 1. Теоремы о пропорциональных отрезках

Видео:Пропорциональные отрезкиСкачать

1.1. Теорема Фалеса

1.1.1. Исторические сведения о Фалесе Милетском

Фалес Милетский (ок. 624 — ок. 546 до н.э.) — греческий философ и математик из Милета. Представитель ионической натурфилософии и основатель милетской школы. Считался одним из семи мудрецов Греции. В Египте занимался изучением причин наводнений, нашел способ измерения высоты пирамид. Считал материю одушевленной. Пытаясь определить основу материального мира, пришел к выводу о том, что ею является вода 1 .

Хотя принято считать, что западная философия начинается с греков однако первые философские системы возникли не в самой Греции а на западном побережье Малой Азии — в ионийских городах, которые были основаны греками и в которых раньше, чем в самой Греции получили развитие промышленность, торговля и духовная культура Этот район еще называют Ионией, поэтому философские системы разработанные философами — выходцами из этого района, носят название ионийской философии. Впервые философские воззрения возникли в Милете в VI-V веках до Р.Х. Милет в то время был крупнейшим из всех малоазиатских греческих городов. Фалес происходил из знатного рода. В своей жизни и творчестве соединял вопросы практики с теоретическими проблемами, касающимися вопросов мироздания. Он много путешествовал по разным странам используя эти путешествия для расширения и приобретения знания Был всесторонним ученым и мыслителем, изобрел несколько астрономических приборов. Стал известен в Греции тем, что удачно предсказал солнечное затмение в 585 г. до Р.Х. Все свои натурфилософские познания Фалес использовал для создания стройного философского учения. Так, он считал, что все существующее порождено водой, понимая под ней влажное первовещество. Вода — это источник, из которого все постоянно происходит. При этом вода и все, что из нее произошло, не являются мертвыми, они одушевлены. В качестве примера своей мысли Фалес приводил такие вещества как магнит и янтарь: так как магнит и янтарь порождают движение значит они обладают душой. Фалес представлял весь мир одушевленным, пронизанным жизнью. Он заложил теоретические основы учения, имеющее название гилозоизм. Хотя гилозоизм имеет свои корни в мифологии, у Фалеса он получает философское обоснование. По Фалесу, природа, как живая, так и неживая, обладает движущим началом, которое называется такими именами, как душа и Бог. В области науки Фалесу принадлежит заслуга в определении времени солнцестояний и равноденствий, в установлении продолжительности года в 365 дней, открытие факта движения Солнца по отношению к звездам. Он также имеет заслуги в области создания научной математики. Так, считают, что он первым сумел вписать треугольник в круг. Все это принесло Фалесу славу первого мудреца из знаменитых «семи мудрецов» древности.

1.1.2. Формулировка и доказательство теоремы Фалеса

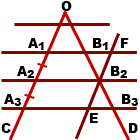
Теорема Фалеса : если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 2

Пусть на прямой l ₁ отложены равные отрезки А ₁ А ₂ , А ₂ А ₃ , А ₃ А ₄ , …и через их концы проведены параллельные прямые, которые пересекают прямую l ₂ в точках В ₁ , В ₂ , В ₃ , В ₄ , … (рис.1). Требуется доказать, что отрезки В ₁ В ₂ , В ₂ В ₃ , В ₃ В ₄ , … равны друг другу. Докажем, например, что В ₁ В ₂ = В ₂ В ₃ .

Рассмотрим сначала случай, когда прямые l ₁ и l ₂ параллельны (рис. 1-а). Тогда А ₁ А ₂ = В ₁ В ₂ и А ₂ А ₃ = В ₂ В ₃ как противоположные стороны параллелограммов А ₁ В ₁ В ₂ А ₂ и А ₂ В ₂ В ₃ А ₃ , так как А ₁ А ₂ = А ₂ А ₃ , то и В ₁ В ₂ = В ₂ В ₃ .

Если прямые l ₁ и l ₂ не параллельны, то через точку В ₁ проведем прямую l , параллельную прямой l ₁ (рис.1, б). Она пересечет прямые А ₂ В ₂ и А ₃ В ₃ в некоторых точках С и D . Так как А ₁ А ₂ = А ₂ А ₃ , то по доказанному В ₁ С = С D . Отсюда получаем В ₁ В ₂ = В ₂ В ₃ . Аналогично можно доказать, что В ₂ В ₃ = В ₃ В ₄ и т.д.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

1.2. Теорема Менелая

1.2.1. Исторические сведения о Менелае Александрийском

Менелай Александрийский, математик и астроном. Время его жизни и деятельности определяется приведенными в «Алмагесте» Птолемея двумя астрономическими наблюдениями, которые Менелай произвел в Риме в первом году царствования Траяна, т. е. в 98 г. после Р. Х.

Менелаем были написаны два сочинения: «О вычислении хорд», в 6 книгах, и «Сферика», в 3 книгах. Из них первое совсем не дошло до нас. Утрачен также и греческий оригинал второго, содержание которого известно современной науке по его латинским переводам, составленным по взаимно подтверждающим друг друга арабским и еврейским переводам того же сочинения. Главным предметом «Сферики» М. служит сферическая тригонометрия. Из числа многих предложений, для нас впервые встречающихся в этом сочинении, самым замечательным считается обыкновенно теорема Менелая, которая прежде называлась правилом шести количеств. Менелай, известен еще и как геометр, работавший в области изучения кривых высших порядков 3 .

1.2.2. Формулировка и доказательство теоремы Менелая

Эта теорема (вместе с обратной) показывает закономерность, наблюдающуюся для отношений отрезков, соединяющих вершины некоторого треугольника и точки пересечения секущей со сторонами (продолжениями сторон) треугольника.

На чертежах приведены два возможных случая расположения треугольника и секущей. В первом случае секущая пересекает две стороны треугольника и продолжение третьей, во втором – продолжения всех трех сторон треугольника.

Теорема 1. (Менелая) Пусть пересечен прямой, не параллельной стороне АВ и пересекающей две его стороны АС и ВС соответственно в точках В ₁ и А ₁ , а прямую АВ в точке С ₁ тогда

Теорема 2. (обратная теореме Менелая) Пусть в треугольнике АВС точки А ₁ , В ₁ , С ₁ принадлежит прямым ВС, АС, АВ соответственно, тогда, если

,

Доказательство первой теоремы можно провести так: на секущую прямую опускают перпендикуляры из всех вершин треугольника. В результате получают три пары подобных прямоугольных треугольников. Фигурирующие в формулировке теоремы отношения отрезков заменяют на отношения перпендикуляров, соответствующих им по подобию. Оказывается, что каждый отрезок – перпендикуляр в дробях будет присутствовать дважды: один раз в одной дроби в числителе, второй раз, в другой дроби, в знаменателе. Таким образом, произведение всех этих отношений окажется равным единице.

Обратная теорема доказывается методом «от противного». Предполагается, что при выполнении условий теоремы 2 точки А ₁ , В ₁ , С ₁ не лежат на одной прямой. Тогда прямая А ₁ В ₁ пересечет сторону АВ в точке С ₂ , отличной от точки С ₁ . При этом, в силу теоремы 1, для точек А ₁ , В ₁ , С ₂ будет выполняться то же отношение, что и для точек А ₁ , В ₁ , С ₁ . Из этого следует, что точки С ₁ и С ₂ поделят отрезок AB в одинаковых отношениях. Тогда эти точки совпадут – получили противоречие 4 .

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

1.3. Теорема Чевы

1.3.1. Исторические сведения о Джованни Чеве

Чева Джованни, (7 декабря 1647 — 15 июня 1734) — итальянский математик и инженер . Главными предметами его занятий были геометрия и механика. Он написал сочинения: » De lineis rectis se invicem secantibus statica constructio » (Милан, 1678); » Opuscula mathematica de potentiis obliquis , de pendulis et vasis et de fluminibus » (там же, 1682); » Tria problemata geometrica proposita » (Мантуя, 1710); » Hydrostatica etc .» (там же, 1728) и несколько других. Самым замечательным из них было первое. В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек. Прилагаемый к вопросам, в которых рассматриваются отношения между отрезками, образованными пересекающимися линиями друг на друге, он состоит в помещении в точках пересечения тяжестей, обратно пропорциональных соответствующим отрезкам, и в последующем за тем выводе отношения между тяжестями на основании принципа рычага в статике. Достаточно назвать известное в геометрии под именем теоремы Чевы предложение о произведениях отрезков, образованных на сторонах треугольника трансверсалями, проходящими через общую точку (произведение трех отрезков, не сходящихся попарно в одной общей точке, равно произведению трех других отрезков), и на подобное же предложение об отрезках, образованных на сторонах четырехугольника плоскостью, их пересекающею, если не все вершины четырехугольника лежат в одной плоскости. Во второй части идеи и теоремы, изложенные в 1-й, прилагаются к коническим сечениям. Наконец, прибавление занимается теоремами о площадях некоторых плоских фигур и об объемах и центрах тяжести тел вращения второго порядка 5 .

1.3.2. Формулировка и доказательство теоремы Чевы

Большинство замечательных точек треугольника могут быть получены при помощи следующей процедуры. Пусть имеется некоторое правило, согласно которому мы сможем выбрать определенную точку A ₁ , на стороне BC (или её продолжении) треугольника ABC (например, выберем середину этой стороны). Затем построим аналогичные точки B ₁ , C ₁ на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора удачное, то прямые AA ₁ , BB ₁ , CC ₁ пересекутся в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в одной точке).

Хотелось бы иметь какой-нибудь общий метод, позволяющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет.

Универсальное условие, «закрывшее» эту проблему, нашёл в 1678 г. итальянский инженер Джованни Чева .

Определение. Отрезки, соединяющие вершины треугольника с точками на противолежащих сторонах (или их продолжениях), называют чевианами, если они пересекаются в одной точке.

Возможны два варианта расположения чевиан. В одном варианте точка

пересечения – внутренняя, а концы чевиан лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного чевиана лежит на стороне, а у двух других чевиан концы лежат на продолжениях сторон (смотри чертежи).

Теорема 3. ( Прямая теорема Чевы) В произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А ₁ , В ₁ , С ₁ , такие, что прямые АА ₁ , ВВ ₁ , СС ₁ пересекаются в некоторой общей точке, тогда

.

Доказательство: известно несколько оригинальных доказательств теоремы Чевы, мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Запишем соотношение теоремы Менелая первый раз для треугольника ABB ₁ и секущей CC ₁ (точку пересечения чевиан обозначим Z ):

,

а второй раз для треугольника B ₁ BC и секущей AA ₁ :

.

Перемножив два этих отношения, проведя необходимые сокращения получим соотношение, содержащееся в утверждении теоремы.

Теорема 4. (Обратная теорема Чевы) . Если для выбранных на сторонах треугольника ABC или их продолжениях точек A ₁ , В ₁ и C ₁ выполняется условие Чевы:

,

Доказательство этой теоремы проводится методом от противного, также, как доказательство теоремы Менелая 6 .

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Глава 2. Практическое применение теорем о пропорциональных отрезках

Видео:Пропорциональные отрезкиСкачать

2.1. Применение теоремы Фалеса

Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N . Докажите, что AN = NC .

Через точку С проведем прямую, параллельную прямой АВ и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 2). Так как AM = МВ по условию, а MB = CD как противоположные стороны параллелограмма BCDM , то АМ = DC . Треугольники АМ N и CDN равны по второму признаку равенства треугольников (АМ= CD , CD секущими АС и М D ), поэтому AN = NC .

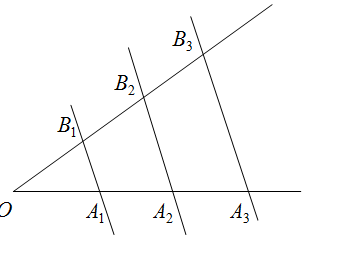
Разделите данный отрезок АВ на n равных частей.

Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно n равных отрезков АА ₁ , А ₁ А ₂ , …, А _{n -1} А _n (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рис. 3 n =5). Проведем прямую А _n В (точка А _n – конец последнего отрезка) и построим прямые, проходящие через точки А ₁ , А ₂ , …, А _{n -1} и параллельные прямой А _n В. Эти прямые пересекают отрезок АВ в точках В ₁ , В ₂ , …, В _{n -1} , которые по теореме Фалеса делят отрезок АВ на n равных частей.

Разделите данный отрезок АВ на 8 равных частей.

Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно 8 равных отрезков АА ₁ , А ₁ А ₂ , …, А ₇ А ₈ (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (рис. 4). Проведем прямую А ₈ В (точка А ₈ – конец последнего отрезка) и построим прямые, проходящие через точки А ₁ , А ₂ , …, А ₇ и параллельные прямой А ₈ В. Эти прямые пересекают отрезок АВ в точках В ₁ , В ₂ , …, В ₇ , которые по теореме Фалеса делят отрезок АВ на 8 равных частей.

Дан треугольник АВС. На стороне ВС взята точка Р так, что ВР=РС, а на стороне АС взята точка Q такая, что А Q : Q С = 5 : 3. Найдите отношение АО : ОР, если точка О – точка пересечения прямых АР и В Q .

Проведем прямые параллельные ВQ через точки А, Р и С. Точка D – это точка пересечения прямых АР и с.

По теореме Фалеса параллельные прямые ВQ, b и c, которые отсекают равные отрезки ВР и РС, отсекают равные отрезки ОР и РD на прямой АD.

По теореме Фалеса параллельные прямые a, BQ и с, которые отсекают на прямой АС отрезки в соотношении 5 : 3, отсекают и на прямой АD отрезки в соотношении 5 : 3.

То есть AQ : QC= 5:3 и AO : OD = 5:3, а отрезок OD=2OP. Следовательно, AO : OP = 10:3.

Разделите данный отрезок АВ на два отрезка АХ и ХВ, пропорциональные данным отрезкам P ₁ Q ₁ и P ₂ Q ₂ .

Проведем какой-нибудь луч АМ, не лежащий на прямой АВ, и на этом луче отложим последовательно отрезки АС и CD , равные отрезкам P ₁ Q ₁ и P ₂ Q ₂ . Затем проведем прямую BD и прямую, проходящую через точку С параллельно прямой BD . Она по теореме Фалеса пересечет отрезок АВ в искомой точке Х.

Видео:Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

2.2. Применение теоремы Чевы и Менелая

I . Задачи на замечательные точки треугольника

Доказать, что биссектрисы треугольника пересекаются в одной точке.

Дано: , – биссектрисы .

Доказать, что биссектрисы и пересекаются в одной точке – точке .

Решение с использованием теоремы Чевы.

Биссектриса треугольника делит противоположную сторону этого треугольника на отрезки, пропорциональные прилежащим сторонам треугольника.

Так как по условию – биссектриса , то:

Так как по условию – биссектриса , то:

Так как по условию – биссектриса , то:

Перемножая получившиеся равенства (3), (1) и (2), получаем, что:

Отсюда по теореме Чевы, биссектрисы пересекаются в одной точке – точке . Доказано.

Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Дано: , – медианы .

медианы и пересекаются в одной точке – точке ;

.

Решение с использованием теорем Чевы и Менелая).

Так как по условию – медианы , то , , , поэтому:

Отсюда по теореме Чевы, медианы пересекаются в одной точке – точке .

Рассмотрим .

Прямая пересекает две стороны ( , ) и продолжение третьей ( – луч, ), значит, по теореме Менелая:

Рассматривая теорему Менелая для и секущей , а также для и секущей , мы получим, что:

Итак, все три медианы пересекаются в точке и делятся ею в отношении , считая от вершины. Доказано.

II. Задачи на пропорциональные отрезки.

В на стороне взята точка так, что . На продолжении стороны за точку взята точка так, что . Прямая пересекает сторону в точке . Найти отношение .

Дано: , , , – луч, , , .

Найти отношение .

Решение c использованием теоремы Менелая

Пусть , тогда по условию ( ): ; пусть , тогда по условию ( ): .

Прямая пересекает две стороны ( , ) и продолжение третьей ( – луч, ), значит, по теореме Менелая:

Ответ: .

На стороне взята точка , а на стороне взята точка , причём . Точка пересечения отрезков и делит в отношении , считая от точки . Найти отношение .

Дано: , , , , , .

Найти отношение .

Решение c использованием теоремы Менелая.

Пусть , тогда по условию ( ): ; пусть , тогда по условию ( ): .

Прямая пересекает две стороны ( , ) и продолжение третьей ( – луч, ), значит, по теореме Менелая:

Ответ: .

III. Задачи на отношение площадей.

Пусть медиана . На медиане взята точка так, что . Прямая разбивает на два треугольника: и , причём . Найти отношение .

Дано: , – медиана , , , – прямая, .

Найти отношение .

Решение c использованием теоремы Менелая.

Пусть , тогда по условию ( медиана ): ; пусть , тогда по условию ( ): .

Рассмотрим и . Основания и лежат на одной прямой (прямой ), а вершина общая. Поэтому у этих треугольников будет и общая высота , значит,

Прямая пересекает две стороны (, ) и продолжение третьей ( – луч, ), значит, по теореме Менелая:

Ответ: .

Биссектрисы и пересекаются в точке . Найти , если , , .

Дано: ; , – биссектрисы , , , , .

Найти .

Решение с использованием теоремы Менелая.

Пусть , тогда по условию (, ):

Так как – биссектриса по условию, то (биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника):

То есть, если , то

Так как – биссектриса по условию, то (биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника):

То есть, если , то

Прямая пересекает две стороны (, ) и продолжение третьей ( – луч, ), значит, по теореме Менелая:

То есть, если , то .

Рассмотрим и .

и имеют общий угол – , поэтому площади этих треугольников относятся как произведения сторон, заключающих .

По условию задачи , поэтому,

Рассмотрим и .

Основания и лежат на одной прямой (прямой ), а вершина общая. Поэтому у этих треугольников будет и общая высота , значит,

Ответ: .

Видео:Теорема о пропорциональных отрезках. Теорема ФалесаСкачать

Заключение

Как показывает история исследования некоторых математических алгоритмов решения задач, которыми пользовались древние вавилоняне и египтяне, современные учёные не могут взять в толк, каким образом они могли быть найдены. Нашим современникам кажется, что для решения задач по нахождению площадей геометрических фигур, объёмов тел и прочих параметров требуются знания высших разделов математики – алгебры интегрально-дифферециального исчисления.

Решение геометрических задач различными способами является исследовательской частью данной работы и дает возможность сравнить разные способы решения и проанализировать их появление.

Решение задач с помощью теорем Фалеса, Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными.

Теоремы Чевы и Менелая также помогают быстро и оригинально решить задачи повышенной сложности.

Видео:ТЕОРЕМА ФАЛЕСА . §11 геометрия 8 классСкачать

Список используемой литературы.

Аксёнова М. Энциклопедия для детей. Том 11. Математика/ В. Володин. – М.: Аванта+, 2004.

Геометрия, 7-9. / Л. С. Атанасян, В.Ф.Бутузов, С.В.Кадомцев и др., – М.: Просвещение, 2011.

Атанасян Л.С. Геометрия. Дополнительные главы к школьным учебникам 8, 9 классов: Учебное пособие для учащихся школ и классов с углублённым изучением математики/ В.Ф. Бутузов, С.Б. Кадомцев, С.А. Шестаков, И.И. Юдина. –12–е издание.– М.: Просвещение, 2002.

Мадер В.В. Полифония доказательств. – М.: Мнемозина, 2009.

Прасолов В.В. Задачи по планиметрии. Часть I. – M.: МЦНМО, 2001.

Звавич Л.И. Геометрия в таблицах. 7-11 классы. – М.: Дрофа, 2003.

Глейзер Г.И. История в математики в школе. – М.: Просвещение, 1983.

Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона [Электронный ресурс] – Режим доступа: http://dic.academic.ru/contents.nsf/brokgauz_efron/

1 Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона [Электронный ресурс] – Режим доступа: http://dic.academic.ru/contents.nsf/brokgauz_efron/

2 Геометрия, 7-9. / Л. С. Атанасян, В.Ф.Бутузов, С.В.Кадомцев и др., – М.: Просвещение, 2011.

3 Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона [Электронный ресурс] – Режим доступа: http://dic.academic.ru/contents.nsf/brokgauz_efron/

4 Атанасян Л.С. Геометрия. Дополнительные главы к школьным учебникам 8, 9 классов: Учебное пособие для учащихся школ и классов с углублённым изучением математики/ В.Ф. Бутузов, С.Б. Кадомцев, С.А. Шестаков, И.И. Юдина. –12–е издание.– М.: Просвещение, 2002

5 Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона [Электронный ресурс] – Режим доступа: http://dic.academic.ru/contents.nsf/brokgauz_efron/

6 Атанасян Л.С. Геометрия. Дополнительные главы к школьным учебникам 8, 9 классов: Учебное пособие для учащихся школ и классов с углублённым изучением математики/ В.Ф. Бутузов, С.Б. Кадомцев, С.А. Шестаков, И.И. Юдина. –12–е издание.– М.: Просвещение, 2002

💡 Видео

Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать