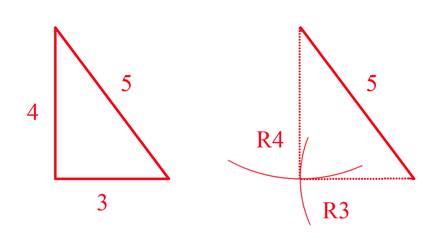Видео:Как разделить угол на равные части с помощью циркуляСкачать

Два одинаковых значения
Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.
При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.
Видео:Построение пятиугольника циркулемСкачать

Получение четырех частей
В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.
Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.
Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Разложение при помощи циркуля
Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:
- одну — из точки А;
- вторую — из точки Е.
И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.
Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Теорема Фалеса
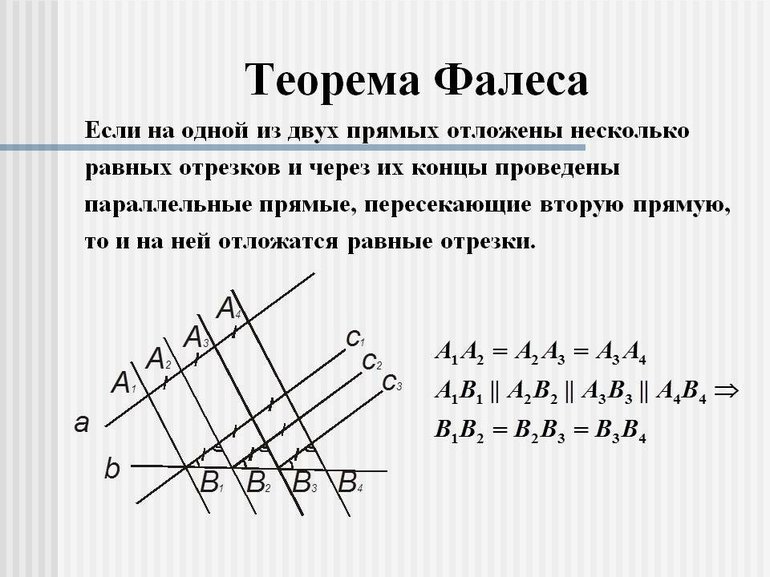
Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.
Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.
Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.
Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия:
- делить прямоугольник на несколько одинаковых прямоугольников;
- разделять треугольник, а соответственно, и его угол на две и более частей;
- рассекать прямой угол на три равных угла;
- разбивать окружность на одинаковые участки.
Все эти знания важны в машиностроении при вычерчивании деталей, а также активно применяются в инженерных работах.
Видео:Деление отрезка циркулем на три части. How to divide a given segment into three parts by a compass.Скачать
Деление отрезка пополам при помощи циркуля
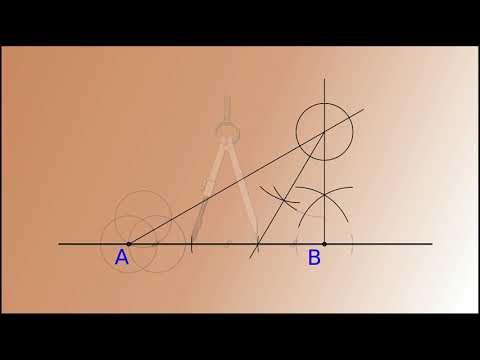
Имеется отрезок произвольной длины. Необходимо разделить его пополам, пользуясь только циркулем и не прибегая к помощи линейки.
По сути, всё, что можно сделать сначала – это прочертить
Из концов отрезка две окружности радиусом равным длине отрезка.
Концы отрезка и точка пересечения окружностей образуют
Пользуясь этим методом можно построить сетку из вспомогательных точек сколь угодно большого размера. Нам потребуется всего два ряда точек лежащие на прямой, являющейся продолжением отрезка и параллельной ей прямой проходящей через вершину построенного нами первого треугольника.
В равностороннем треугольнике любая высота (перпендикуляр, проведенный из вершины к противоположной стороне) является одновременно медианой (линией соединяющей вершину и середину противоположной стороны) а значит, чтобы получить
середину отрезка, достаточно провести через вершину треугольника окружность, центр которой лежит на прямой, равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой проходящей через вершину треугольника. Центром окружности может служить середина отрезка, концы которого расположены на вышеупомянутых прямых
Но, по условию задачи, пользоваться линейкой мы не можем
(все линии на рисунках начерчены лишь для пояснения), а значит
в окончательном построении нам придется пользоваться лишь точками из верхнего и нижнего рядов или точкой из верхнего ряда и точкой лежащей на исходном отрезке. Концы вспомогательного отрезка соединить линией мы тоже не сможем, поэтому его центр нам придется получать тоже с помощью единственно циркуля.
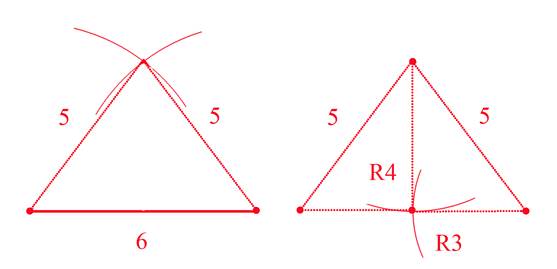
Тут нам на помощь придет теорема Пифагора, а точнее её частный случай со сторонами треугольника 3,4 и 5.Угол между сторонами
3 и 4 – прямой, и, следовательно, если мы возьмем отрезок, равный
5 и из одного конца прочертим окружность радиусом 3, а из другого радиусом 4, получим прямоугольный треугольник.
И как следствие мы можем, зная это, получить середину отрезка длиной 6, пользуясь только циркулем.
Применив эти построения к нашему случаю, получим такую методу:
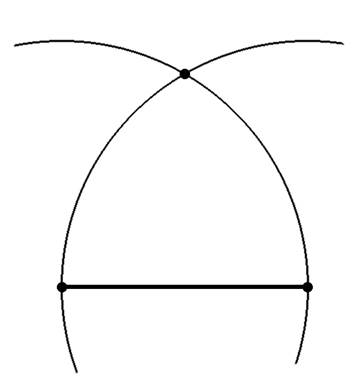
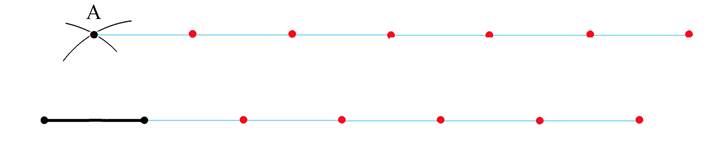
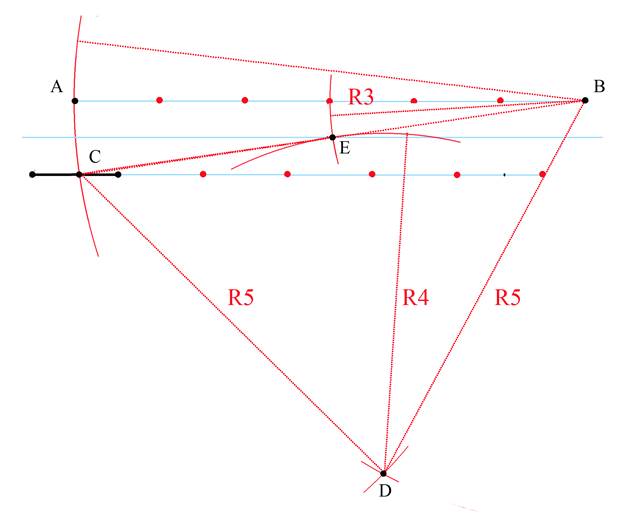
1.Проведя из концов исходного отрезка дуги окружностей радиусом
равным длине отрезка получим на их пересечении точку A– вершину равностороннего треугольника.
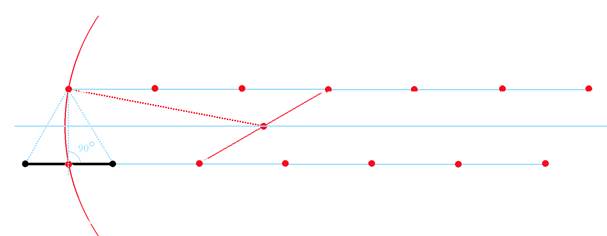
2.Сходным образом построим два ряда точек, обозначенных на
рисунке красным. Расстояние между двумя соседними точками равно длине исходного отрезка – условной единице. Точки верхнего ряда лежат на одной прямой и нижнего ряда – аналогично.
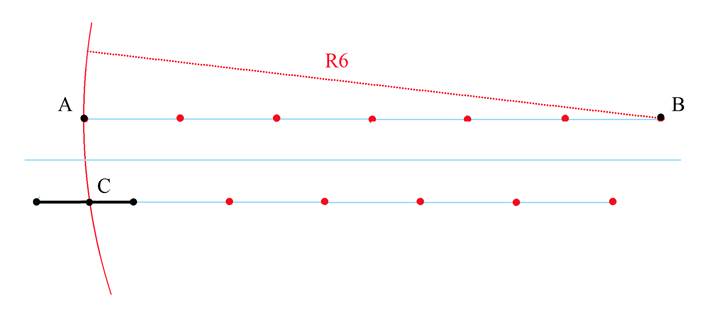
3.Отсчитав от точки А шестую точку, обозначим ее B.
Из точки B проведем дугу окружности радиусом BA= 6
На пересечении этой дуги с исходным отрезком отметим точку C.
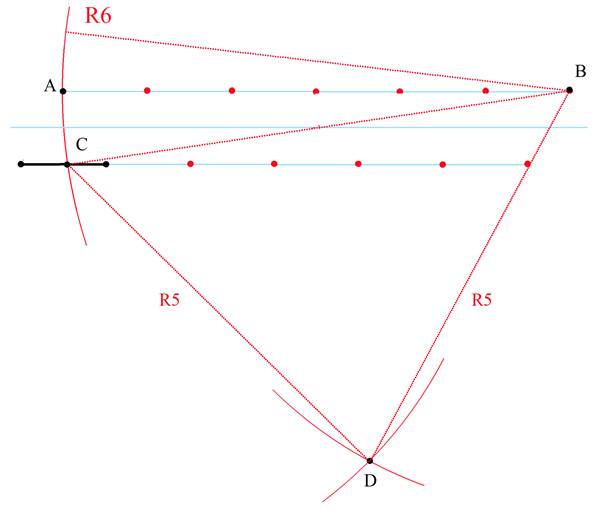
4.Отложим от точки В пять точек и этим радиусом проведем дугу окружности. Этим же радиусом проведем дугу из точки С.
Точку пересечения этих дуг обозначим D.
DC=DB, треугольник CDB – равнобедренный
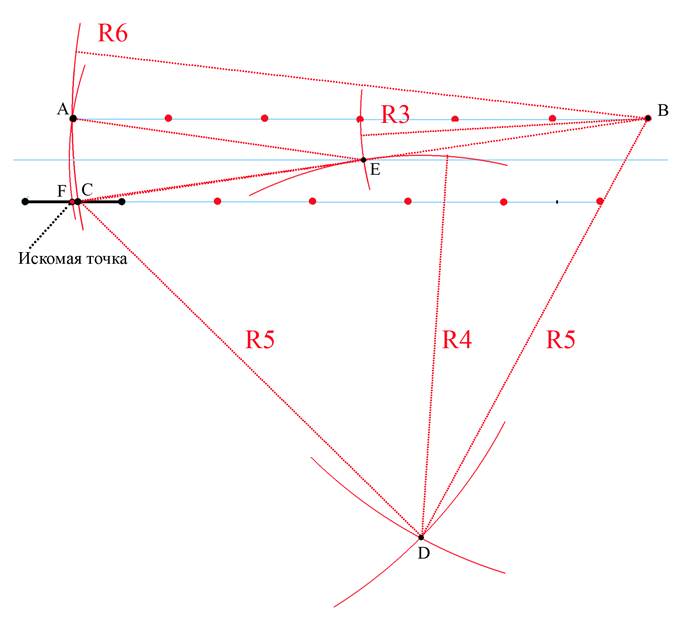
5. Из точки В проведем дугу радиусом 3 а из точки D радиусом 4.
На пересечении дуг получим точку Е – середину отрезка ВС.
Как мы ранее обосновали, точка Е, являясь серединой отрезка ВС,
(как следствие теоремы Пифагора), лежит на прямой , равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой, проходящей через точку А,
а значит равноудалена от точки А и искомой точки, являющейся серединой исходного отрезка. Следовательно, приняв ее за центр
и проведя окружность через точку А, на пересечении этой окружности с исходным отрезком получим искомую точку.
6. Что мы и сделаем.
Точка F и есть искомая точка – середина исходного отрезка
Таким образом, задача деления отрезка пополам решается при помощи одного лишь циркуля.
Это станет видно, когда мы уберем из рисунка вспомогательные лини, с помощью которых иллюстрировалось объяснение и
покажем окружности, использовавшиеся для построения промежуточных точек, ранее не показанные, чтобы не отвлекать от объяснения.
Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 396 Атанасян 8 классСкачать
Как разделить отрезок на равные части — формулы и способы
С одной стороны, разделить отрезок на равные части несложно, но с другой стороны, при этом могут появиться и трудности. Разбить какой-либо промежуток на равные части требуется не только для решения задач по геометрии, но и во многих областях жизни. В бытовой ситуации, например, такое деление может потребоваться для того, чтобы повесить картину на стене или установить мебельный гарнитур в определённой части комнаты.
Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Два одинаковых значения
Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.
При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Получение четырех частей
В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.
Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.
Видео:🧭Как разделить круг на ТРИ Части, без Линейки и Циркуля; How to split a circle into three partsСкачать

Разложение при помощи циркуля
Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:
- одну — из точки А;
- вторую — из точки Е.
И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.
Видео:Геометрия - Построение правильного треугольникаСкачать

Теорема Фалеса
Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.
Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.
Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.
Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия:
- делить прямоугольник на несколько одинаковых прямоугольников;
- разделять треугольник, а соответственно, и его угол на две и более частей;
- рассекать прямой угол на три равных угла;
- разбивать окружность на одинаковые участки.
Все эти знания важны в машиностроении при вычерчивании деталей, а также активно применяются в инженерных работах.
💡 Видео
Построение медианы в треугольникеСкачать

Деление окружности на равные части с помощью циркуляСкачать

Строим треугольник по трем сторонам (Задача 5).Скачать

Построение биссектрисы в треугольникеСкачать

Деление окружности на 5 частей с помощью циркуляСкачать
Построение 8 угольника циркулемСкачать

Деление отрезка на 2,4,8 равных частей с помощью циркуля и линейкиСкачать

Деление окружности на 12 равных частейСкачать

Деление окружности на 3 равные частиСкачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать