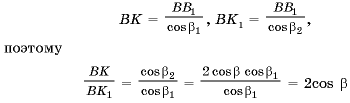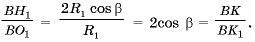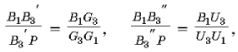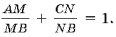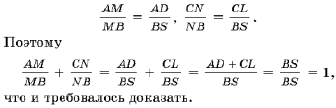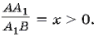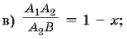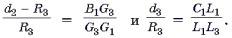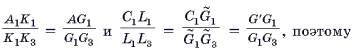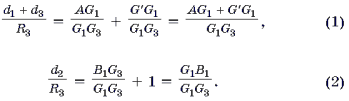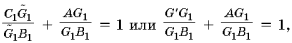Теорема об окружности эйлера (4 видео) | Курс школьной геометрии

Окружность девяти точек и прямая Эйлера

Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих точку пересечения с вершинами треугольника, лежат на одной окружности девяти точек.

Непрерывно изменяя исходный треугольник, получаем мультфильм.

При гомотетии с центром в ортоцентре треугольника и описанная окружность треугольника переходит в окружность девяти точек.

При этой гомотетии центр описанной окружности переходит в центр окружности девяти точек. Следовательно, центр окружности девяти середина отрезка, соединяющего ортоцентр треугольника с центром его описанной окружности.

При гомотетии с центром в точке пересечения медиан и вершины треугольника переходят в середины противоположных сторон. Поэтому при этой гомотетии высоты переходят в серединные перпендикуляры, а в центр описанной окружности. Это значит, что центр тяжести треугольника (точка пересечения его медиан) лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и расположена вдвое ближе к центру описанной окружности, чем к ортоцентру.

Таким образом, центр описанной окружности, центр тяжести, центр окружности девяти точек и ортоцентр лежат на одной прямой Эйлера.

Вот как меняется прямая Эйлера при движении вершин треугольника.

А вот так выглядят прямая Эйлера и окружность девяти точек, изображённые на одном рисунке.

Содержание

О прямых Эйлера и окружности девяти точек
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
📹 Видео

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

О прямых Эйлера и окружности девяти точек

Рассмотрим сначала следующую задачу.

Дан непрямоугольный треугольник ABC с высотами AA₁, BB₁ и CC₁. Докажите, что прямые Эйлера (см. ниже) треугольников AB₁C₁, A₁BC₁, A₁B₁C пересекаются в такой точке P окружности девяти точек треугольника ABC, для которой один из отрезков PA₁, PB₁, PC₁ равен сумме двух других отрезков.

Автором этой задачи является известный французский геометр Виктор Тебо, а ее решение приведено в [1]. В нашей статье будет рассказано про некоторые обобщения данной задачи.

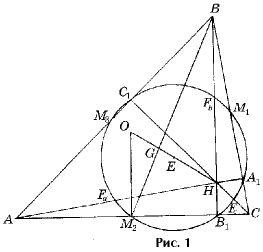
1. Докажите, что для произвольного неравностороннего треугольника ABC его ортоцентр (точка пересечения высот) H, точка пересечения медиан G и центр O описанной окружности лежат на одной прямой, называемой прямой Эйлера этого треугольника, причем OG : GH = 1 : 2 (рис. 1).

2. Докажите, что середины сторон треугольника ABC, основания его высот и середины отрезков, соединяющих ортоцентр с вершинами треугольника, лежат на одной окружности, которая называется окружностью девяти точек треугольника ABC. Центр этой окружности совпадает с серединой отрезка OH, а ее радиус равен половине радиуса описанной окружности треугольника ABC (рис. 1).

3. Докажите, что радиус описанной окружности и высота треугольника, проходящие через одну из его вершин, образуют равные углы со сторонами треугольника, пересекающимися в той же вершине.

4. Пусть AA₁, BB₁, CC₁ – высоты непрямоугольного треугольника ABC, Р BAC = a , Р CBA = b , Р ACB = g . Докажите, что:

5. Докажите, что прямая Эйлера остроугольного треугольника пересекает его наибольшую и наименьшую стороны, а прямая Эйлера тупоугольного треугольника – его наибольшую и среднюю стороны.

Заметим, что решение упражнения 2 можно найти в [2], а упражнения 4 б) – в [1].

Лемма 1. Прямая Эйлера треугольника ABC пересекает его стороны AB и BC в точках M и N соответственно. Тогда прямая Эйлера треугольника MBN параллельна стороне AC.

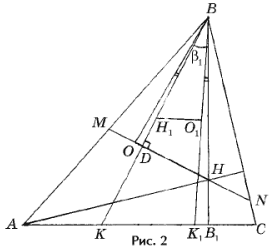
Доказательство. Предположим, что D ABC остроугольный (рис. 2), тогда из упражнения 5 следует, что AB и BC – наибольшая и наименьшая стороны D ABC (будем считать для определенности, что AB > BC). Пусть H и H₁ – ортоцентры, O и O₁ – центры, а R и R₁ – радиусы описанных окружностей треугольников ABC и MBN; D – основание высоты BD треугольника MBN, Р ABC = b , Р DBH = b ₁, Р DBO = b ₂.

Поскольку Р MBO = Р NBH и Р MBD = Р NBO₁ (упражнение 3), то Р HBO₁ = Р DBO = b ₂. Из упражнения 4а) следует, что BH = 2Rcos b , поэтому из прямоугольных треугольников OBD и HBD

BD = BO cos b ₂ = Rcos b ₂ = BH cos b ₁ = 2R cos b cos b ₁, откуда cos b ₂ = 2cos b cos b ₁.

С другой стороны, из прямоугольных треугольников KBB₁ и K₁BB₁

Таким образом, D BH₁O₁ » D BKK₁ и H₁O₁ || KK₁. На рис. 2 точка D принадлежит отрезку OH. Случай, когда точка D лежит вне отрезка OH, разберите самостоятельно.

6. Проведите доказательство леммы 1 для тупоугольного треугольника.

7. Прямая Эйлера треугольника параллельна одной из его сторон.

а) произведение тангенсов углов, прилежащих к этой стороне, равно 3;
б) данный треугольник остроугольный.

8. Докажите, что прямая Эйлера разностороннего

а) остроугольного треугольника ABC отсекает от него остроугольный треугольник T, причем средние по величине углы треугольников ABC и T совпадают;
б) Тупоугольного треугольника ABC отсекает от него разносторонний тупоугольный треугольник T, причем минимальные углы треугольников ABC и T совпадают.

9. Докажите, что если один из углов остроугольного треугольника равен 60°, то прямая Эйлера этого треугольника отсекает от него правильный треугольник.

10. Докажите, что если ни один из углов разностороннего остроугольного треугольника не равен 60°, то прямая Эйлера этого треугольника отсекает от него разносторонний остроугольный треугольник.

Определение. Пусть прямая Эйлера треугольника ABC не проходит ни через одну из его вершин и отсекает от него треугольник T₁, прямая Эйлера треугольника T₁ отсекает от него треугольник T₂, …, прямая Эйлера треугольника T_n–1 – треугольник T_n (n = 1, 2, 3, …, T₀ = D ABC). Назовем прямой Эйлера порядка n или n–прямой Эйлера треугольника ABC прямую Эйлера треугольника T_n–1.

Ясно, что 1–прямая Эйлера треугольника совпадает с прямой Эйлера этого треугольника. Поскольку прямая Эйлера равнобедренного или прямоугольного треугольника проходит через одну из его вершин, то для этих треугольников n-прямые Эйлера не определены при n > 1. Из упражнений 8–10 следует, что для всех остальных треугольников n–прямые Эйлера определены для любых натуральных n, за исключением таких остроугольных треугольников ровно один из углов которых равен 60°. В самом деле, для остроугольного треугольника с одним из углов в 60° n–прямая Эйлера не определена при n l 2 (упражнение 9).

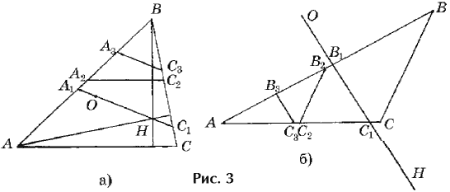
Из определения n–прямых Эйлера и леммы 1 вытекает, что все n–прямые Эйлера нечетного порядка параллельны друг другу и прямой Эйлера треугольника ABC, а все n–прямые Эйлера четного порядка параллельны друг другу и одной из сторон треугольника ABC (средней для остроугольного треугольника и наименьшей для тупоугольного, рис. 3).

В дополнение к обозначениям упражнения 4 будем считать, что в D ABC a b g , H – ортоцентр, F _a , F _b , F _c – середины отрезков AH, BH, CH.

Теорема 1. Дан разносторонний остроугольный треугольник ABC, ни один из углов которого не равен 60°. Тогда точки пересечения прямых Эйлера порядка n треугольников AB₁C₁, A₁BC₁, A₁B₁C являются при n > 1 вершинами треугольников T_n, подобных треугольнику ABC, причем при четных n треугольники T_n гомотетичны друг другу и треугольнику A₁BC₁ с центром гомотетии в точке F_b, а при нечетных n – гомотетичны друг другу с центром гомотетии в точке P.

Доказательство. Поскольку ни один из углов разностороннего остроугольного D ABC не равен 60°, то его n–прямые Эйлера определены для всех натуральных n.

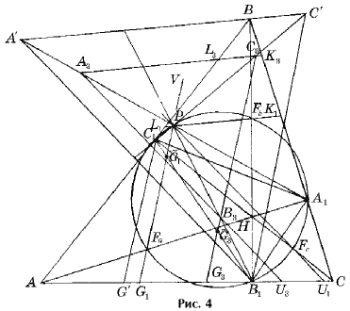
Рассмотрим сначала n = 3. Напомним, что в силу принятых обозначений Р CBA = b – средний по величине угол D ABC (рис. 4). Треугольники AB₁C₁, A₁BC₁, A₁B₁C подобны D ABC (упражнение 4 а) и, значит, n–прямые Эйлера этих треугольников также определены для любых натуральных n, причем Р C₁BA₁ = Р AB₁C₁ = Р CB₁A₁ = b – средние по величине углы в треугольниках AB₁C₁, A₁BC₁,

A₁B₁C. Поскольку прямые Эйлера этих треугольников пересекаются в точке P, лежащей на окружности девяти точек D ABC (упражнение 4 б), то Р F_aPF_c = Р F_aF_bF_c, как вписанные, опирающиеся на одну и ту же дугу окружности девяти точек. Но Р F_aF_bF_c = Р ABC = b , так как D F_aF_bF_c гомотетичен D ABC с центром гомотетии в точке H и коэффициентом 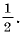. Аналогично

т. е. острые углы между прямыми Эйлера треугольников AB₁C₁, A₁BC₁, A₁B₁C равны углам треугольника ABC, а поскольку по лемме 1 3–прямые Эйлера этих треугольников параллельны их прямым Эйлера, то и углы треугольника T₃ = A₃B₃C₃ равны углам D ABC, откуда следует их подобие.

Покажем теперь, что вершины треугольника T₃ лежат на прямых, соединяющих точку P с точками A₁, B₁, C₁. Пусть G₁, G₃, U₁, U₃ – соответственно точки пересечения прямой Эйлера и 3–прямой Эйлера треугольников AB₁C₁ и CB₁A₁ со стороной AC (рис. 4), а B₃ R и B₃ RR – точки пересечения 3–прямых Эйлера этих треугольников с отрезком PB₁. Тогда

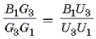
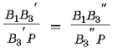
так как G₃B₃ R || G₁P и U₃B₃ RR || U₁P. Но в силу подобия треугольников AB₁C₁ и CB₁A₁, поэтому и B₃ R є B₃ RR є B₃, т. е. точка B₃ пересечения 3–прямых Эйлера треугольников AB₁C₁ и CB₁A₁ лежит на отрезке PB₁.

Аналогично показывается, что точки A₃ и C₃ лежат на прямых PA₁ и PC₁. Понятно, что доказательство этих фактов для произвольного треугольника T_{2l + 1} будет точно таким же.

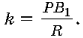
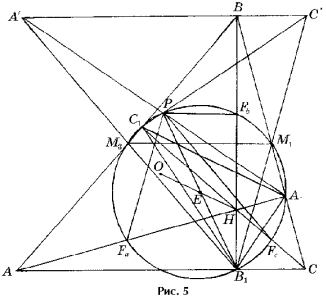
При l ® Ґ треугольники T_{2l + 1} стремятся к предельному треугольнику D ₁ = A R B₁C R , одна из вершин которого совпадает с B₁. Поскольку радиусы описанных окружностей треугольников D ₁ и ABC равны PB₁ и R, то коэффициент подобия треугольника D ₁ треугольнику ABC равен Но точки P и B₁ лежат на окружности девяти точек D ABC, поэтому хорда PB₁ не превосходит диаметра этой окружности, равного R (упражнение 2) и k Ј 1.

Выясним, когда k = 1. При k = 1 PB₁ = R, т. е. хорда PB₁ является диаметром и Р PF_bB₁ = 90° = Р PF_bB. Так как F_b – центр описанной окружности D A₁BC₁, подобного D ABC, то это означает, что данному условию удовлетворяют треугольники ABC, прямая Эйлера которых перпендикулярна диаметру описанной окружности, проходящему через вершину среднего угла D ABC. Для таких треугольников ABC треугольник D ₁ симметричен D ABC относительно средней линии, параллельной стороне AC (рис. 5).

Итак, в любом случае коэффициенты подобия треугольников T_{2l + 1} и ABC меньше единицы, и ни один из треугольников T_{2l + 1} не может быть равен D ABC.

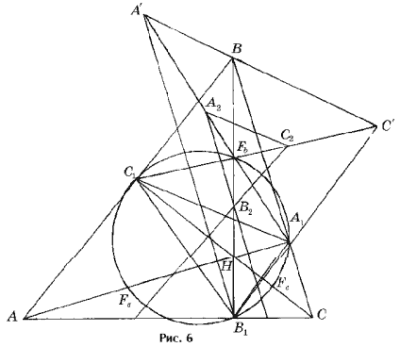
Доказательство для треугольников T_n с четными номерами аналогично приведенному выше. В этом случае коэффициент подобия предельного треугольника D ₂ треугольнику ABC равен cos ( g – a ) a g , рис. 6).

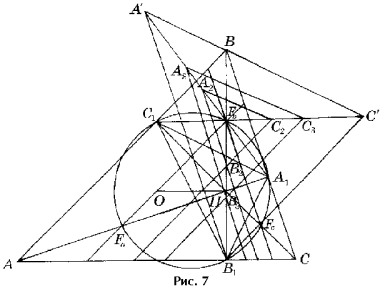
Заметим, что если прямая Эйлера D ABC параллельна стороне AC, то точка P совпадает с точкой F_b и все треугольники T_n имеют общий центр гомотетии F_b (рис. 7).

Утверждение теоремы 1 справедливо и для произвольных разносторонних тупоугольных треугольников ABC со следующим незначительным изменением в случае четных n: треугольники T_2m гомотетичны друг другу и D AB₁C₁ с центром гомотетии в точке F_a. Укажем еще на некоторые отличия от остроугольного треугольника: для тупоугольного D ABC коэффициенты гомотетии треугольников T_2m и D AB₁C₁ могут менять знак (с положительного на отрицательный), т. е. треугольники T_2m как бы совершают «кульбит». Если рассмотреть три тупоугольных треугольника ABC, ACH, BCH, где H – ортоцентр D ABC, а треугольник ABH – разносторонний, то для двух из них центры гомотетии треугольников T_2m совпадают, а коэффициенты гомотетии треугольников T_2m не меняют знак лишь для одного из треугольников ABC, ACH, BCH (здесь одинаково обозначены через T_2m элементы трех последовательностей T_2m (1) , T_2m (2) , T_2m (3) , треугольников ABC, ACH, BCH, m = 1, 2, …, напомним, что в D ABC тупым является угол ACB). Поскольку прямая Эйлера тупоугольного треугольника не параллельна ни одной из его сторон (упражнение 7), то для тупоугольного треугольника центры гомотетии треугольников T_2m и T_{2l + 1} (m, l = 1, 2, …) не могут совпадать.

Попытайтесь самостоятельно разобраться в приведенных здесь фактах.

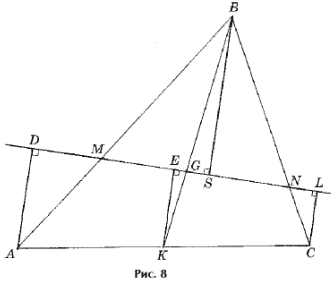
Лемма 2. Прямая, проходящая через точку G пересечения медиан треугольника ABC, пересекает его стороны AB и BC в точках M и N.

Тогда

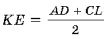
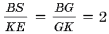
Доказательство. Пусть D, E, S, L – основания перпендикуляров, опущенных соответственно из точек A, K, B, C на прямую MN (рис. 8, K – середина AC). Тогда как средняя линия прямоугольной трапеции ACLD. Из подобия прямоугольных треугольников KEG и BSG следует, что (напомним, что G – точка пересечения медиан треугольника ABC). Итак,

Из подобия прямоугольных треугольников ADM и BSM, CLN и BSN выводим, что

11. В разностороннем остроугольном треугольнике ABC Р ABC = 60°, прямая Эйлера этого треугольника пересекает его стороны AB и BC в точках M и N. Докажите, что AM + CN = MN.

12. Найдите геометрическое место центров тяжести всевозможных треугольников BAC, угол BAC которых общий, а сумма сторон AB и BC постоянна (AB + BC = d > 0).

13. Пусть n–прямые Эйлера треугольника ABC пересекают его стороны AB и BC в точках An и Cn (n = 1, 2, 3), причем

тогда и только тогда, когда прямая A1C1 параллельна стороне AC;

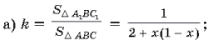
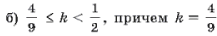
г) коэффициент подобия треугольников A₂BC₂ и ABC равен k;

Теорема 2. Пусть n–прямые Эйлера треугольника ABC определены для любых натуральных n. Тогда сумма расстояний от двух вершин треугольника T_{2l + 1} = A_{2l + 1}B_{2l + 1}C_{2l + 1} до двух одноименных вершин треугольника A₁B₁C₁ равна сумме расстояния между третьими вершинами этих треугольников с утроенным радиусом описанной окружности треугольника T_{2l + 1}.

Доказательство. Рассмотрим остроугольный D ABC (рис. 4). Обозначим через d₁, d₂, d₃, длины отрезков PA₁, PB₁, PC₁, а через R₃ – радиус описанной окружности D A₃B₃C₃. Тогда, поскольку PF_b || A₃C₃, получаем по теореме Фалеса 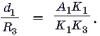. Аналогично

Из подобия треугольников A₁BC₁ и B₁AC₁ следует, что

Так как прямая Эйлера треугольника проходит через точку пересечения его медиан (упражнение 1), то по лемме 2

откуда G R G₁ + AG₁ = G₁B₁. Подставив найденное выражение в (1) и учитывая (2), получим

Видео:Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Please wait.

Видео:16 задание. Профильный ЕГЭ 2023. 9 точек окружности, окружность Эйлера. Что это?Скачать

We are checking your browser. mathvox.ru

Видео:Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6cb346311efd75b3 • Your IP : 85.95.179.65 • Performance & security by Cloudflare