- Линейная скорость вращения, частота и частота угловая
- Число оборотов
- Угловая скорость
- Описывающие вращение физические величины
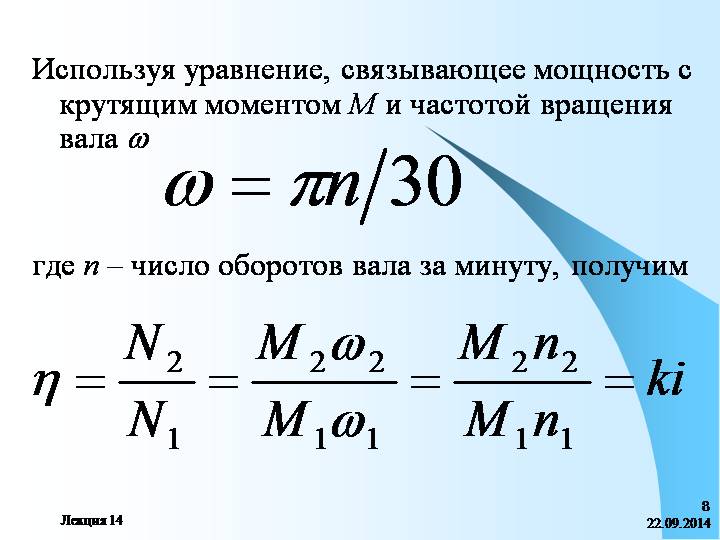
- Мощность вращающихся объектов
- Задача на определение циклической частоты вращения вала
- Линейная скорость вращения, частота и частота угловая
- Коэффициент полезного действия электромотора
- Угловая частота, период и угловая скорость
- Переменный синусоидальный ток
- Угловая частота, период и угловая скорость
- Вращательное движение тела, формулы
- Экономическое обоснование эффекта от инвертора
- Основные формулы расчета мощности двигателей
- Угловая скорость в спорте
- Описывающие вращение физические величины
- Описывающие вращение физические величины
- Как подключить частотный преобразователь
- Циклическая частота вращения (обращения)
- Задача на определение циклической частоты вращения вала
- Период пульсаций и частота
- Интенсивность циклов
- Опасность разночастотных зарядов
- Генерирование переменного тока
- Инвертор
- Фазорасщепитель
- Формулы частоты вращения циклической. Определение частоты вращения вала
- Что такое вращение?
- Описывающие вращение физические величины
- Угловая частота, период и угловая скорость
- Линейная скорость вращения, частота и частота угловая
- Задача на определение циклической частоты вращения вала
- Скалярное и векторное управление асинхронными двигателями — в чем различие?
Видео:Вращательное движение. 10 класс.Скачать

Линейная скорость вращения, частота и частота угловая
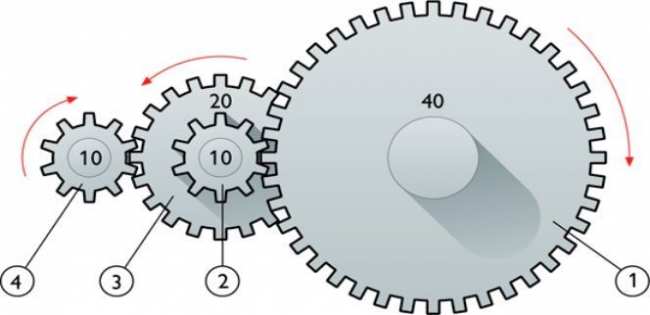
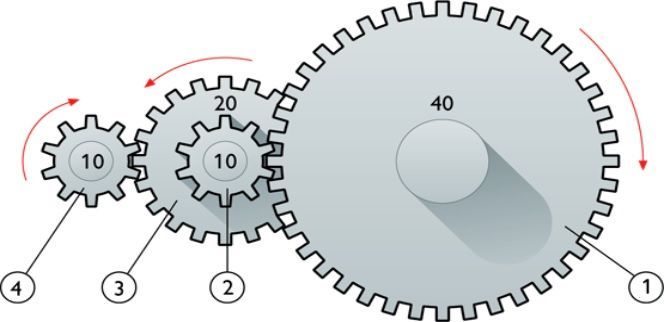
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Видео:Урок 87 (осн). Вращательное движение. Период и частота вращенияСкачать

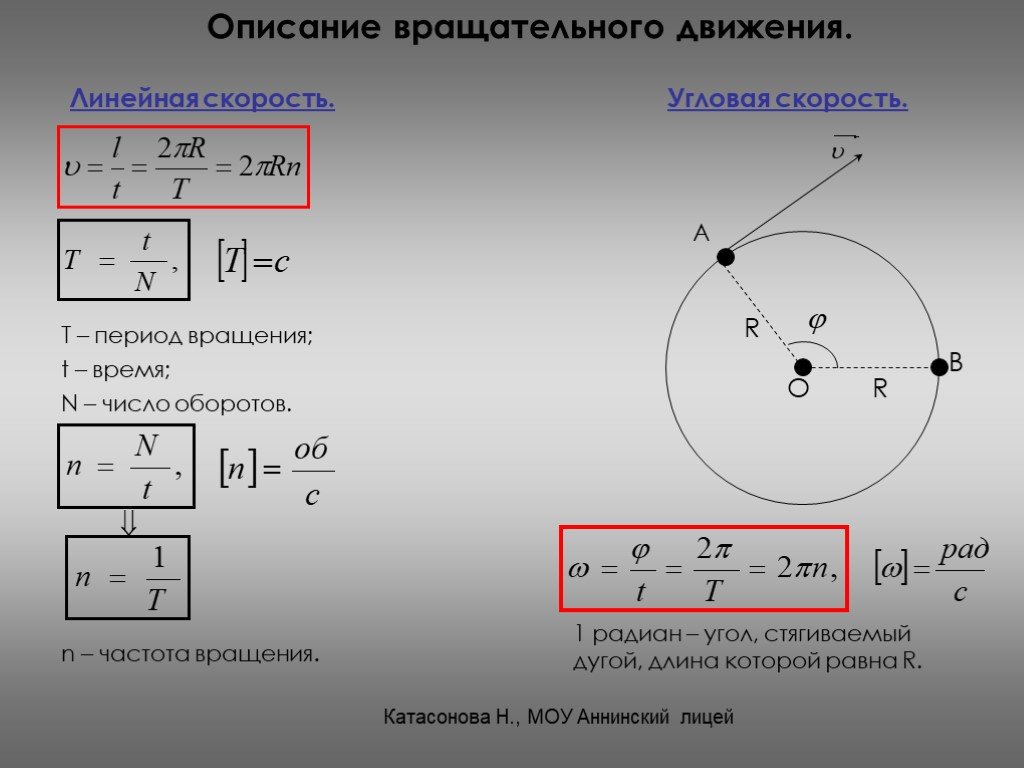
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если n — число оборотов, f — частота, T — продолжительность одного оборота, период, ? — угловое перемещение, N — полное число оборотов, t — время, продолжительность вращения, ? — угловая частота,
то
Угловое перемещение равно произведению полного числа оборотов на 2?:
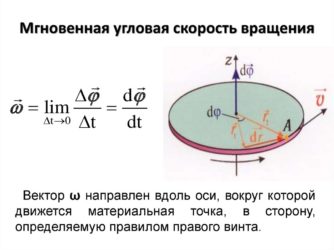
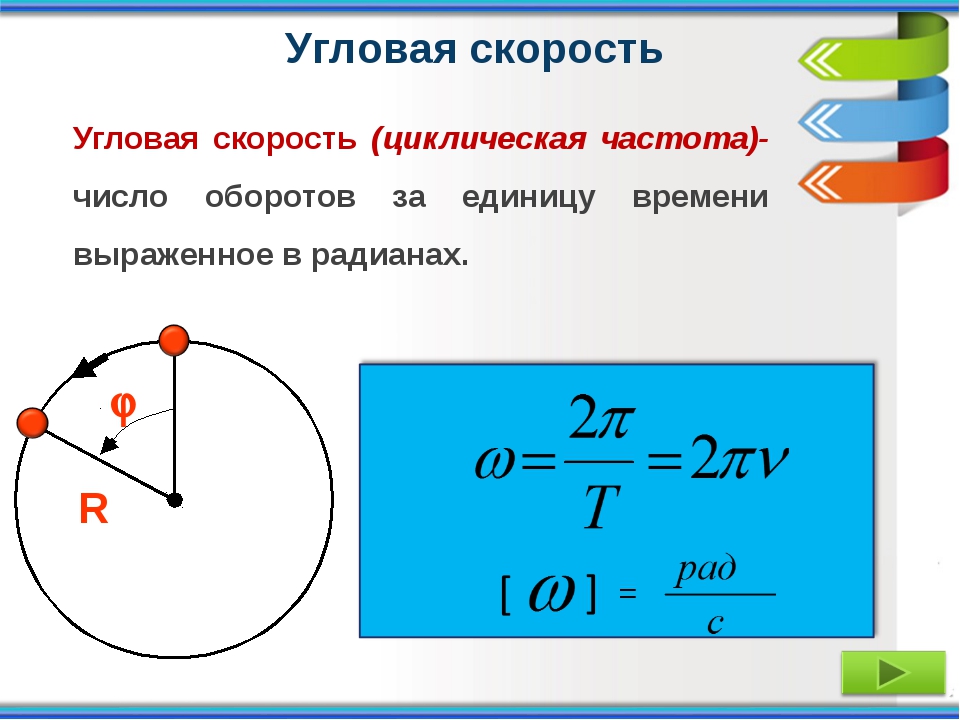
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.• вопреки своему названию число оборотов n — это не число, а физическая величина.• следует различать число оборотов n и полное число оборотов N
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

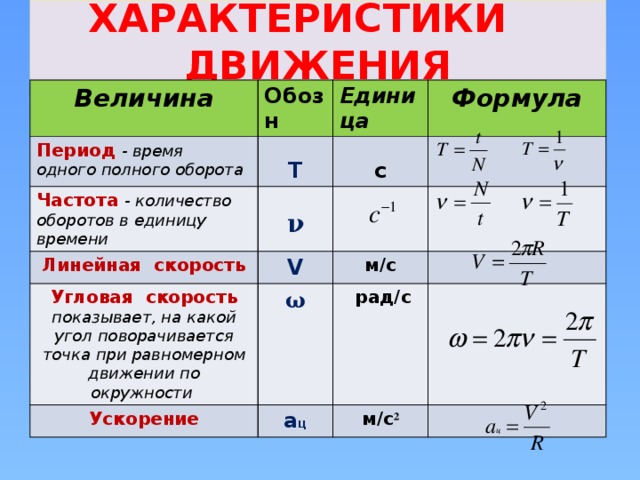
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:







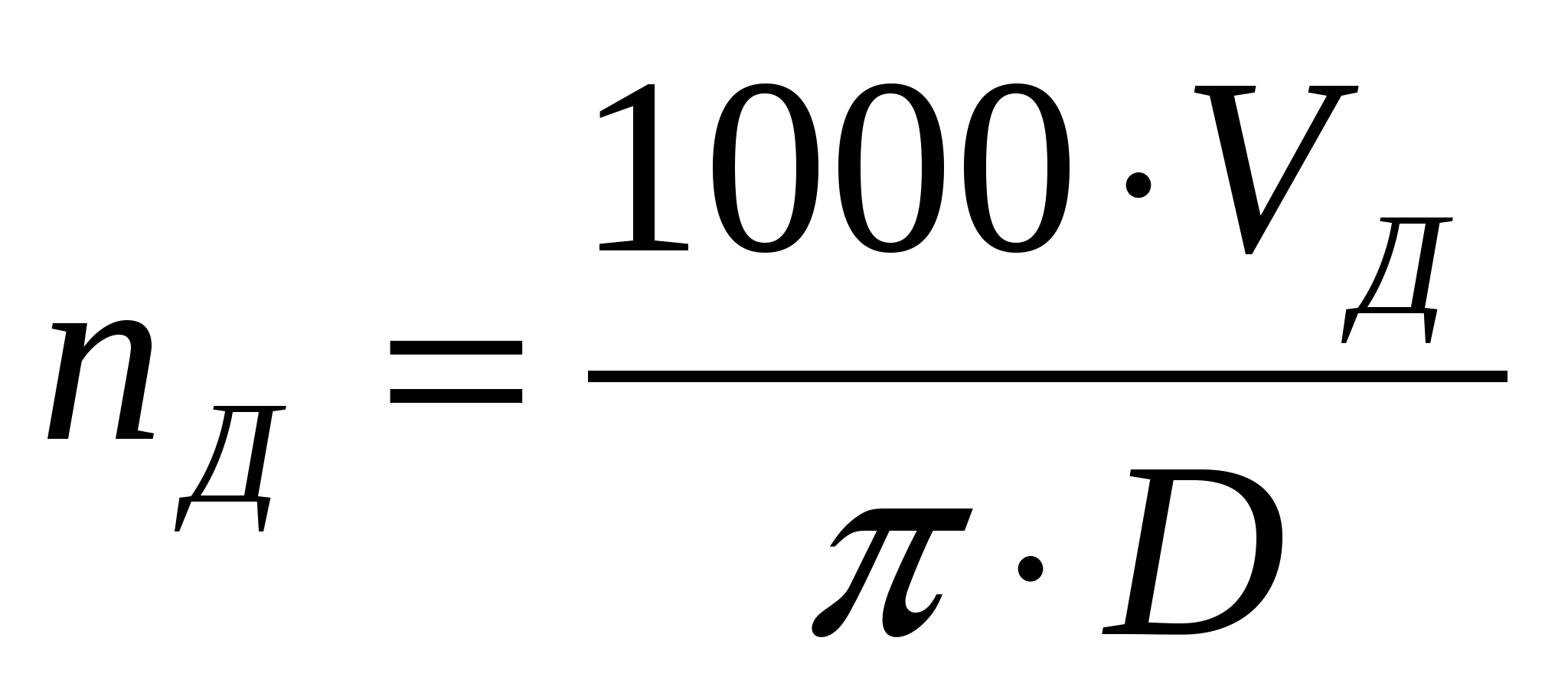
Видео:Физика с нуля. Угловая скорость, период и частота вращения.Скачать

Мощность вращающихся объектов
Для расчета подобной системы применяют формулу:
N = M * w = (2π * M* n)/60,
- M – момент силы;
- w – угловая скорость, характеризующая вращение;
- n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.
Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.
Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Видео:Период и частота обращенияСкачать

Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Коэффициент полезного действия электромотора
КПД — это характеристика, которая отражает эффективность работы системы при преобразовании энергии в механическую. Выражается отношением полезной энергии к потраченной. По единой системе единиц измерений он обозначается как «eta» и является безразмерным значением, исчисляемым в процентах. Формула КПД электродвигателя через мощность:
P1 — электрическая (подаваемая) мощность, Вт;
P2 — полезная (механическая) мощность, Вт;
Также он может быть выражен как:
eta = A ÷ Q × 100 %, где:
A — полезная работа, Дж;
Q — затраченная энергия, Дж.
Чаще коэффициент вычисляют по формуле потребляемой мощности электродвигателя, так как эти показатели всегда легче измерить.
Снижение эффективности работы электродвигателя происходит по причине:
Электрических потерь. Это происходит в результате нагрева проводников от прохождения по ним тока. Магнитных потерь

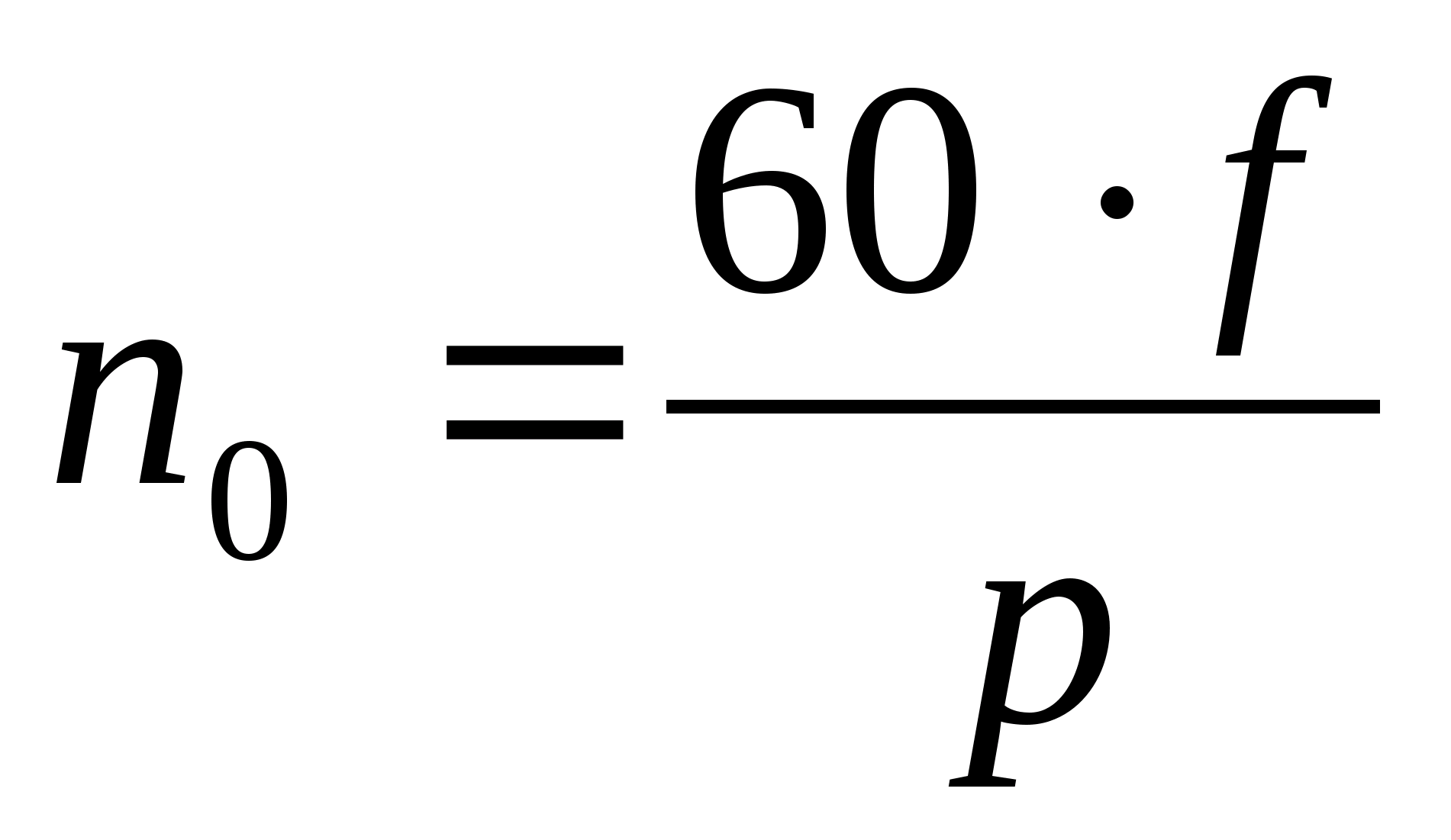




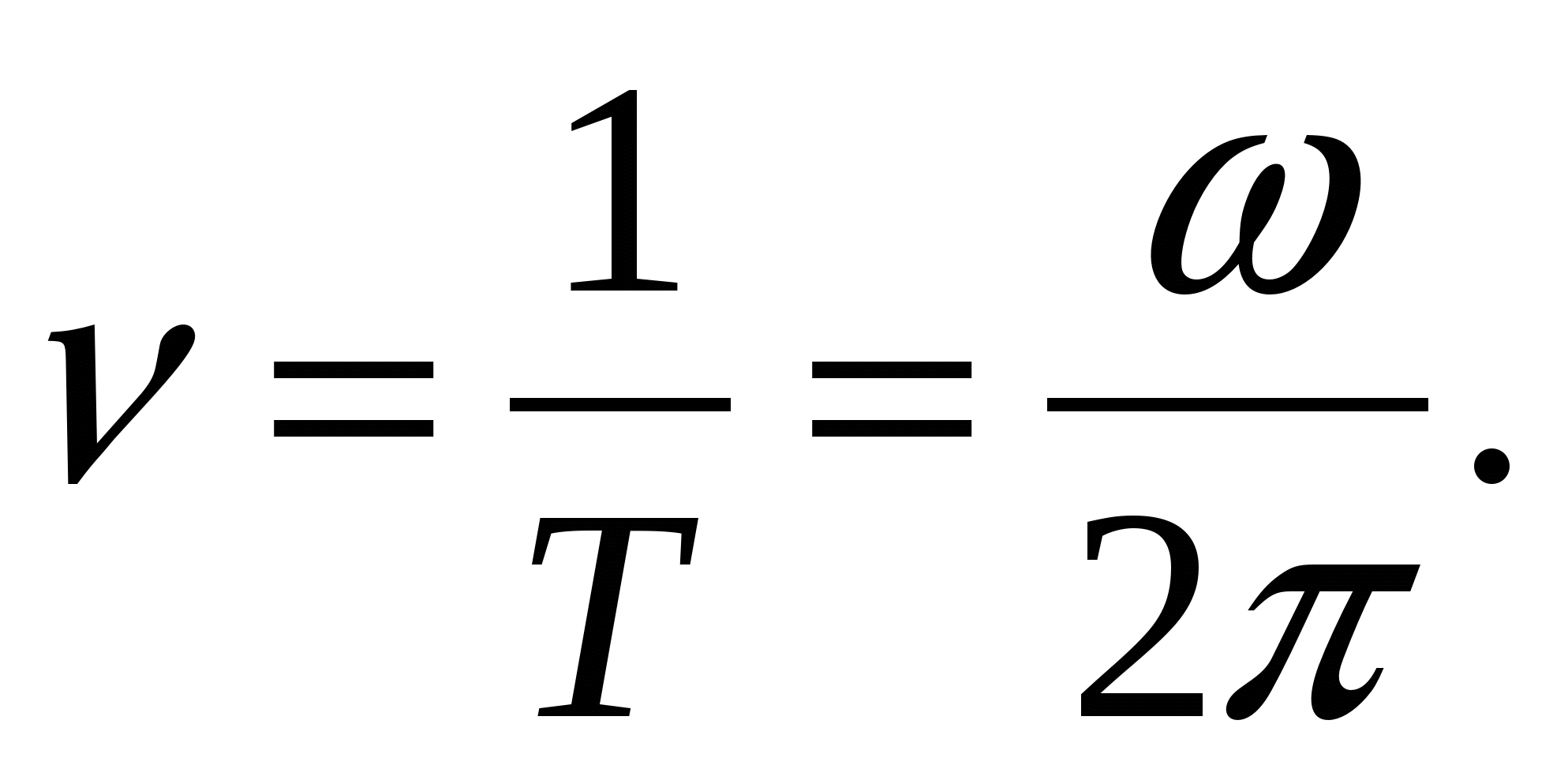

Вследствие излишнего намагничивания сердечника появляется гистерезис и вихревые токи, что важно учитывать в формуле мощности электродвигателя. Механических потерь
Они связаны с трением и вентиляцией. Дополнительных потерь. Они появляются из-за гармоник магнитного поля, так как статор и ротор имеют зубчатую форму. Также в обмотке присутствуют высшие гармоники магнитодвижущей силы.
Следует отметить, что КПД является одним из самых важных компонентов формулы расчета мощности электродвигателя, так как позволяет получить цифры, наиболее приближенные к действительности. В среднем этот показатель варьирует от 10% до 99%. Она зависит от конструктивного устройства механизма.
Видео:Физика - движение по окружностиСкачать

Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Видео:Линейная и угловая скорости при равномерном движении по окружностиСкачать

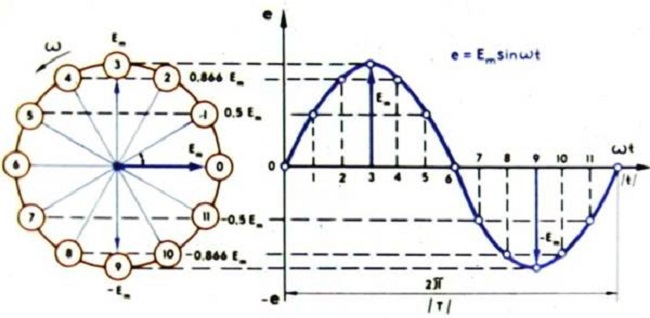
Переменный синусоидальный ток
Это тот ток, который периодически меняется во времени, и его изменения подчиняются закону синусоиды. Это элементарное движение электрических зарядов, потому дальнейшему разложению на простые токи оно не подлежит.
Вид формулы такого переменного тока:
- Im – амплитуда;
- sinωt – фаза синусоидального тока, рад.
Здесь ω = const, называется угловой частотой переменного электричества, причём угол ωt находится в прямой временной зависимости.
Зная частоту f исходного тока, можно вычислить его угловую частоту, применив выражение:
Тут 2π – это выраженное в радианах значение центрального угла окружности:
- Т = 2 π радиан = 3600;
- Т/2 = π = 1800;
- Т/4 = π/2 = 900.
Если выразить 1 рад в градусах, то он будет равен 57°17′.
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения.
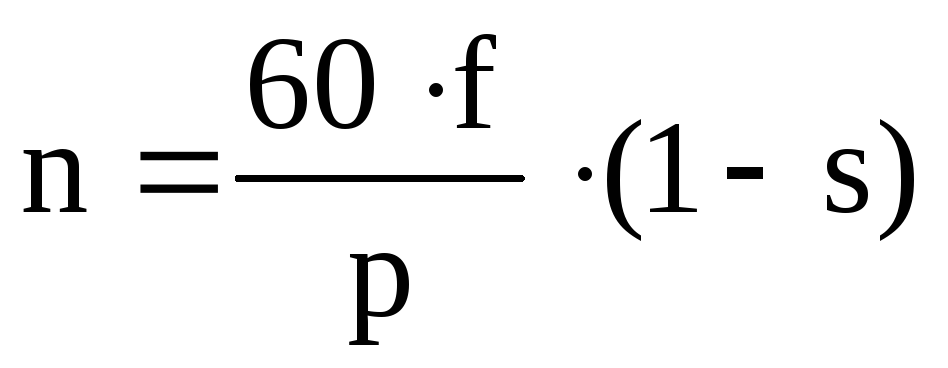




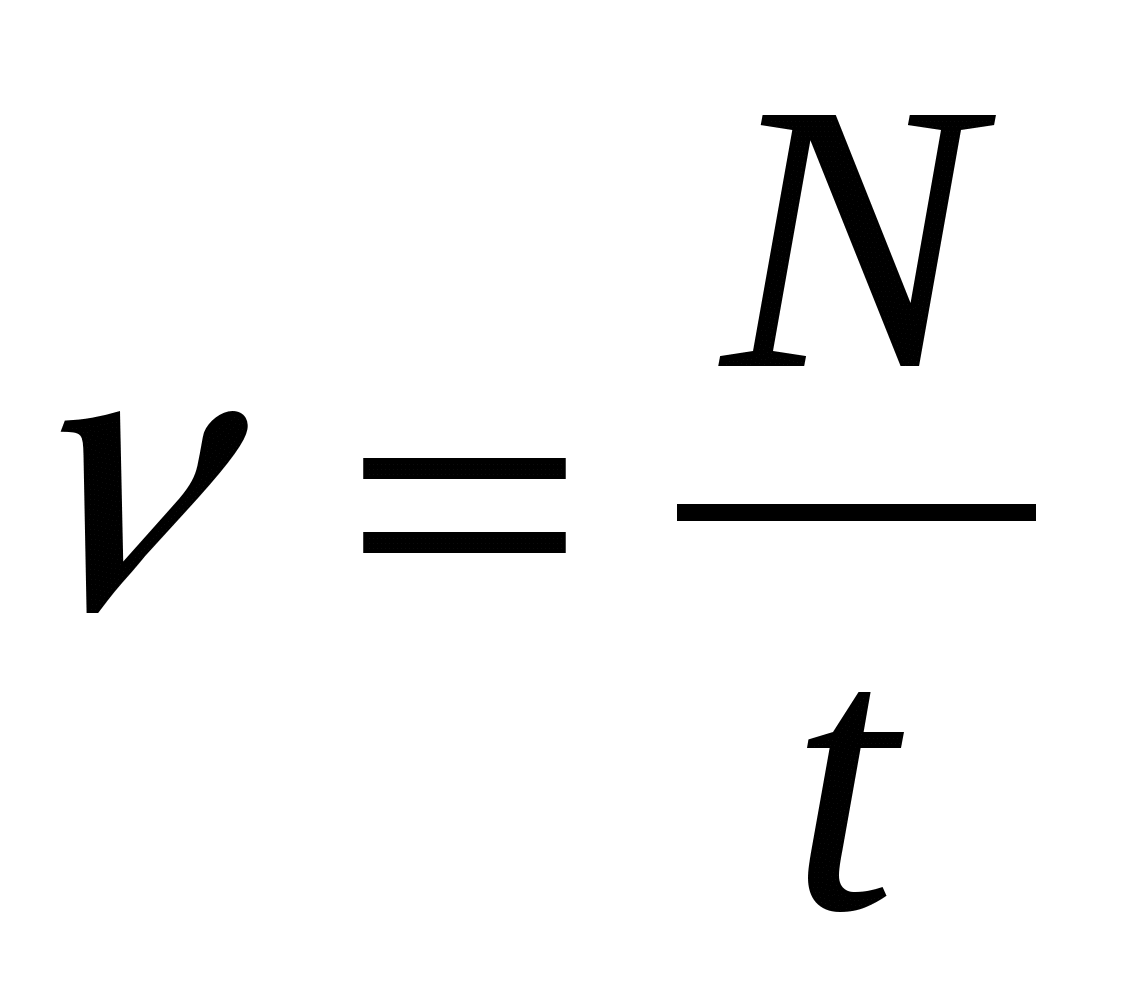

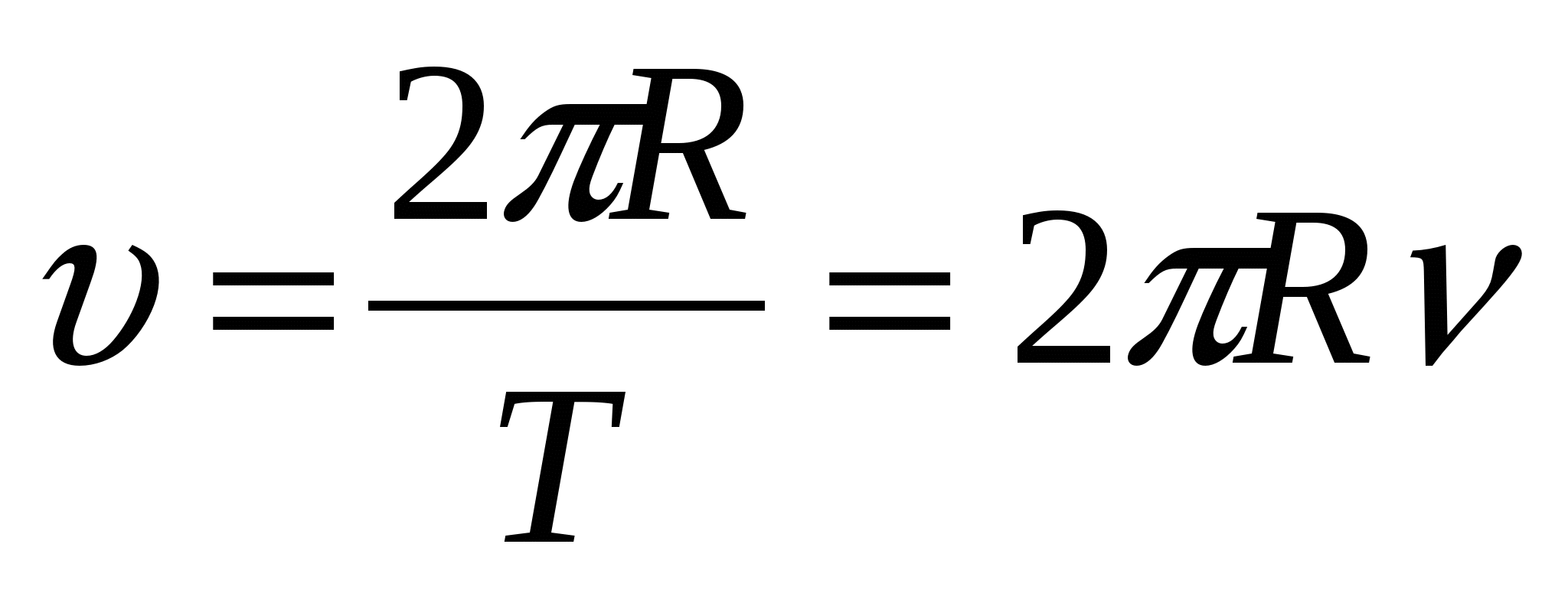
Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями.
Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Видео:Пожалуй, главное заблуждение об электричестве [Veritasium]Скачать
![Пожалуй, главное заблуждение об электричестве [Veritasium]](https://i.ytimg.com/vi/6Hv2GLtnf2c/0.jpg)
Экономическое обоснование эффекта от инвертора
Время окупаемости инвертора рассчитывается отношением затрат на покупку к экономии энергии. Экономия обычно равна от 20 до 40% от номинальной мощности мотора.
Затраты снижают факторы, повышающие производительность частотных преобразователей:
- Уменьшение затрат на обслуживание.
- Повышение ресурса двигателя.
где Э – экономия денег в рублях;
Рпч – мощность инвертора;
Ч – часов эксплуатации в день;
К – коэффициент ожидаемого процента экономии;
Т – тариф энергии в рублях.
Время окупаемости равно отношению затрат на покупку инвертора к экономии денег. Расчеты показывают, что период окупаемости получается от 3 месяцев до 3 лет. Это зависит от мощности мотора.
Модуль №4. Частотное регулирование скорости асинхронного двигателя

Видео:угловая и линейная скоростьСкачать

Основные формулы расчета мощности двигателей
Для вычисления реальных характеристик механизмов всегда нужно учитывать много параметров. в первую очередь нужно знать, какой ток подается на обмотки электродвигателя: постоянный или переменный. Принцип их работы отличается, следовательно, отличаются метод вычислений. Если упрощенный вид расчета мощности привода выглядит как:
U — напряжение, В;
Pэл — подведенная электрическая мощность. Вт.
В формуле мощности электродвигателя переменного тока необходимо также учитывать сдвиг фаз (alpha). Соответственно, расчеты для асинхронного привода выглядят как:
Pэл = U × I × cos(alpha).
Кроме активной (подведенной) мощности существует также:
- S — реактивная, ВА. S = P ÷ cos(alpha).
- Q — полная, ВА. Q = I × U × sin(alpha).
В расчетах также необходимо учитывать тепловые и индукционные потери, а также трение. Поэтому упрощенная модель формулы для электродвигателя постоянного тока выглядит как:
Pэл = Pмех + Ртеп +Ринд + Ртр, где
Рмех — полезная вырабатываемая мощность, Вт;
Ртеп — потери на образование тепла, ВТ;
Ринд — затраты на заряд в индукционной катушке, Вт;
Рт — потери в результате трения, Вт.
Видео:Фаза, начальная фаза и угловая частота переменного токаСкачать

Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.







При первобытнообщинном строе главными охотниками были мужчины

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Видео:Центростремительное ускорение. 9 класс.Скачать

Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Видео:Угловая скорость и радианная мера углаСкачать

Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Видео:Ускорение, период и частота обращенияСкачать

Как подключить частотный преобразователь
Если кабель для подключения на 220 В с 1-й фазой, применяется схема «треугольника». Нельзя подключать частотник, если выходной ток выше 50% от номинального значения.
Если кабель питания на три фазы 380 В, то делается схема «звезды». Чтобы проще было подключать питание, предусмотрены контакты и клеммы с буквенными обозначениями.
- Контакты R, S, T предназначены для подключения сети питания по фазам.
- Клеммы U , V , W служат соединением электродвигателя. Для реверса достаточно изменить подключение двух проводов между собой.
В приборе должна быть колодка с клеммой подключения к земле. Подробней, как подключить, здесь.
Видео:Котика ударило током, 10 т. ВольтСкачать

Циклическая частота вращения (обращения)
Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.
Циклическая частота вращения – это количество оборотов тела за 2*π секунды.
У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.
Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.
При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:
- частоты питающей сети;
- количества пар полюсов.
Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.
Видео:Момент инерцииСкачать

Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?


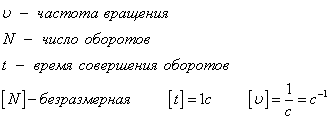





Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Видео:Правое и левое вращение.Скачать

Период пульсаций и частота
Частота переменного тока может иметь другое название – пульсация. Периодом пульсации называют время единичной пульсации.
Интенсивность циклов
Для электросети с частотой 50 Гц период пульсации составит:
При необходимости, зная эту зависимость, можно по времени цикла вычислить частоту.
Опасность разночастотных зарядов
Как постоянный, так и переменный ток при определённых значениях представляет опасность для человека. До 500 В разница в безопасности находится в соотношении 1:3 (42 В постоянного к 120 В переменного).
При значениях выше 500 В это соотношение выравнивается, причём константное электричество вызывает ожоги и электролизацию кожных покровов, изменяющееся – судороги, фибрилляцию и смерть. Тут уже частота пульсации имеет большое значение. Самый опасный интервал частот – от 40 до 60 Гц. Далее с повышением частоты риск поражения уменьшается.

Частота переменного электричества – важный параметр. Она влияет не только на работу электроустановок потребителей, но и на человеческий организм. Изменяя частоту электрических колебаний, можно менять технологические процессы на производстве и качество вырабатываемой энергии.
Генерирование переменного тока
Кроме стандартных генераторов, для производства переменного тока применяются инверторы и фазорасщепители.
Инвертор
Это устройство, с помощью которого из постоянного тока получают его переменный вид. В процессе этого величина выходного напряжения тоже меняется. Схема устройства представляет собой электронный генератор синусоидального импульсного напряжения периодического характера. Есть варианты инверторов, работающих с дискретным сигналом. Инверторы применяют для автономного питания оборудования от аккумуляторов постоянного напряжения.

Фазорасщепитель
Ещё один способ получить несколько фаз из какого-либо сигнала – это выполнить его расщепление на несколько фаз. Это делается с помощью фазорасщепителя. Принудительная обработка сигналов цифрового или аналогового формата используется, как в радиоэлектронике, так и в силовой электротехнике.
Для электроснабжения трёхфазных асинхронных двигателей применяют выполненный на их же базе фазорасщепитель. Для этого обмотки трёхфазного двигателя соединяют не «звездой», а иначе. Две катушки присоединяют между собой последовательно, третью – подключают к средней точке второй обмотки. Двигатель запускают, как однофазный, после разгона в его третьей обмотке наводится ЭДС.
Интересно. В случае расщепления фаз подобным методом сдвиг фаз между 2 и 3 обмоткой составляет не 1200, как должно быть в идеале, а 900.
Формулы частоты вращения циклической. Определение частоты вращения вала
Одним из распространенных в природе и технике видов движения является вращение. Этот вид перемещения тел в пространстве характеризуется набором физических величин. Важная характеристика любого вращения — это частота. Формулу частоту вращения можно найти, зная определенные величины и параметры.
Что такое вращение?
Под ним в физике понимают такое перемещение материальной точки вокруг некоторой оси, при котором ее расстояние до этой оси остается постоянным. Оно называется радиусом вращения.

Примерами этого движения в природе является вращение планет вокруг Солнца и вокруг собственной оси. В технике вращение представлено движением валов, шестеренок, колеса автомобиля или велосипеда, перемещением лопастей ветровых мельниц.
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
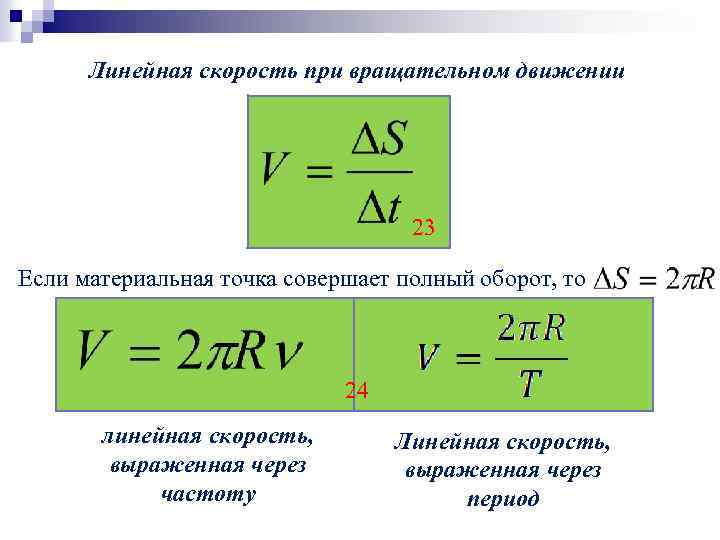
Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
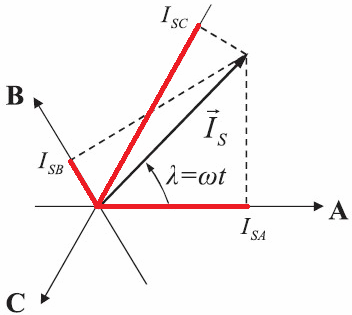
Скалярное и векторное управление асинхронными двигателями — в чем различие?
Асинхронный двигатель — двигатель переменного тока, в котором токи в обмотках статора создают вращающееся магнитное поле. Это магнитное поле индуктирует токи в обмотке ротора и, действуя на эти токи, увлекает за собой ротор.
Однако для того, чтобы во вращающемся роторе вращающееся магнитное поле статора индуктировало токи, ротор в своем вращении должен немного отставать от вращающегося, поля статора. Поэтому в асинхронном двигателе скорость вращения ротора всегда немного меньше скорости вращения магнитного поля (которая определяется частотой переменного тока, питающего двигатель).
Отставание ротора от вращающегося магнитного поля статора (скольжение ротора) тем больше, чем больше нагрузка двигателя. Отсутствие синхронизма между вращением ротора и магнитного поля статора — характерная черта асинхронного двигателя, от которой и происходит его название.
Вращающееся магнитное поле в статоре создается с помощью обмоток, питаемых токами, сдвинутыми по фазе. Обычно для этой цели применяется трехфазный переменный ток. Существуют также однофазные асинхронные двигатели, в которых сдвиг фаз между токами в обмотках создается включением различных реактивных сопротивлений в обмотки.
С целью регулировки угловой скорости вращения ротора, а также крутящего момента на валу современных бесщеточных двигателей, применяют либо векторное, либо скалярное управление электроприводом.
Более всего распространение получило скалярное управление асинхронным двигателем, когда для управления например скоростью вращения вентилятора или насоса, достаточно удерживать постоянной скорость вращения ротора, для этого хватает сигнала обратной связи от датчика давления или от датчика скорости.
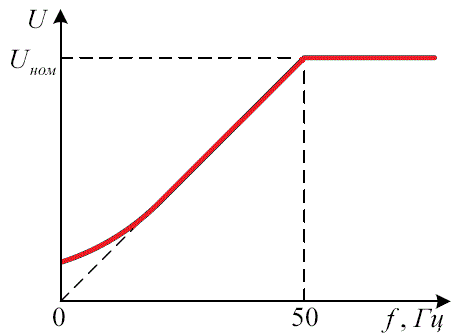
Принцип скалярного управления прост: амплитуда питающего напряжения является функцией частоты, причем отношение напряжения к частоте оказывается приблизительно постоянным.
Конкретный вид этой зависимости связан с нагрузкой на валу, однако принцип остается таковым: повышаем частоту, а напряжение при этом пропорционально повышается в зависимости от нагрузочной характеристики данного двигателя.
В итоге магнитный поток в зазоре между ротором и статором поддерживается почти постоянным. Если же отношение напряжения к частоте отклонить от номинального для данного двигателя, то двигатель либо перевозбудится, либо недовозбудится, что приведет к потерям в двигателе и к сбоям в рабочем процессе.
Таким образом скалярное управление позволяет добиться почти постоянного момента на валу в рабочем диапазоне частот независимо от частоты, однако на низких скоростях момент все же снижается (чтобы этого не произошло, необходимо повысить отношение напряжения к частоте), поэтому для каждого двигателя имеет место строго определенный рабочий диапазон скалярного управления.
Кроме того, невозможно построить систему скалярного регулирования скорости без датчика скорости, установленного на валу, ибо нагрузка сильно влияет на отставание реальной скорости вращения ротора от частоты питающего напряжения. Но даже с датчиком скорости при скалярном управлении не получится с высокой точностью регулировать момент (по крайней мере так, чтобы это было экономически целесообразно).
В этом и заключаются недостатки скалярного управления, объясняющие относительную немногочисленность сфер его применения, ограниченных в основном обычными асинхронными двигателями, где зависимость скольжения от нагрузки не является критичной.
Для избавления от названных недостатков, в далеком 1971 году инженеры компании Сименс предложили использовать векторное управление двигателем, при котором контроль осуществляется с обратной связью по величине магнитного потока. Первые системы векторного управления содержали датчики потока в двигателях.
Сегодня подход к данному методу несколько иной: математическая модель двигателя позволяет рассчитывать скорость вращения ротора и момент на валу в зависимости от текущих токов фаз (от частоты и величин токов в обмотках статора).
Этот более прогрессивный подход предоставляет возможность независимо и почти безынерционно регулировать как момент на валу, так и скорость вращения вала под нагрузкой, ибо в процессе управления учитываются еще и фазы токов.
Некоторые более точные системы векторного управления оснащены схемами обратной связи по скорости, при этом системы управления без датчиков скорости именуются бездатчиковыми.
Так, в зависимости от области применения того или иного электропривода, его система векторного управления будет иметь свои особенности, свою степень точности регулировки.
Когда требования к точности регулировки скорости допускают отклонение до 1,5%, а диапазон регулировки — не превышает 1 к 100, то бездатчиковая система вполне подойдет. Если же требуется точность регулировки скорости с отклонением не более 0,2%, а диапазон сводится до 1 к 10000, то необходимо наличие обратной связи по датчику скорости на валу. Наличие датчика скорости в системах векторного управления позволяет точно регулировать момент даже при низких частотах до 1 Гц.
Итак, векторное управление дает следующие преимущества. Высокую точность управления скоростью вращения ротора (и без датчика скорости на нем) даже в условиях динамически изменяющейся нагрузки на валу, при этом рывков не будет. Плавное и ровное вращение вала на малых скоростях. Высокий КПД в силу низких потерь в условиях оптимальных характеристик напряжения питания.
Не обходится векторное управление без недостатков. Сложность вычислительных операций. Необходимость задавать исходные данные (параметры регулируемого привода).
Для группового электропривода векторное управление принципиально не годится, здесь лучше подойдет скалярное.