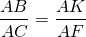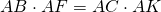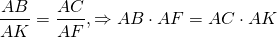Теорема о произведении отрезков секущих окружности

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Свойство секущих

Теорема

Для каждой из секущих, проведённых из одной точки, произведение длины секущей на длину её внешней части есть величина постоянная.

Дано : окружность (O; R), AB и AC — секущие,

AB∩окр. (O; R)=F, AC∩окр. (O; R)=K

Рассмотрим треугольники ABK и ACF.

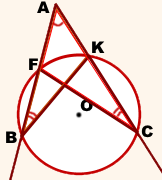
∠ABK=∠ACF (как вписанные углы, опирающиеся на одну дугу FK).

Следовательно, треугольники ABK и ACF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

По основному свойству пропорции:

Что и требовалось доказать.

II способ

1) Проведём отрезки FK и BC.

2) Так как четырёхугольник BFKC — вписанный в окружность, то сумма его противолежащих углов равна 180º:

∠BCK+∠BFK=180º. Следовательно, ∠BFK=180º-∠BCK.

3) ∠AFK+∠BFK=180º (как смежные). Отсюда,

4) Рассмотрим треугольники ABC и AKF.

У них ∠ACB=∠AFK (так как ∠AFK=∠BCK по доказанному), ∠A — общий угол. Следовательно, треугольники ABC и AKF — подобны (по двум углам).

Что и требовалось доказать .

При решении задач будем использовать свойство секущих, а также запомним полученные в ходе доказательства теоремы факты о подобии треугольников, образованных секущими. Причем подобие треугольников ABC и AKF можно доказывать как приведённым выше способом, так и опираясь на свойство секущих.

Справочник репетитора по математике. Свойства окружности и ее элементов

Теоретические справочные материалы по геометрии для выполнения заданий от репетитора по математике. В помощь ученикам при решении задач.

1) Терема о вписанном угле в окружность.

Теорема: вписанный в окружность угол равен половие градусной меры дуги, на которую он опирается (или половине центрального угла, соответствующего данной дуге), то есть .

2) Следствия из теоремы о вписанном угле в окружность.

2.1) Свойство углов, опирающихся на одну дугу.

Теорема: если вписанные углы опираются на одну дугу, то они равны (если они опираются на дополнителные дуги, их сумма равна

2.2) Свойство угла, опирающегося на диаметр.

Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.

AC-диаметр

3) Cвойство отрезков касательных. Окружность, вписанная в угол.

Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.

Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.

4) Свойство отрезков хорд при внутреннем пересечении секущих.
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть

= .

Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть

5) Свойство отрезков хорд при внешнем пересечении секущих.

Теорема 1: произведение отрезков одной секущей равно произведению отрезков другой, то есть

= .

Теорема 2: угол между секущими равен полуразности соответствующих им дуг, то есть

Комментарий репетитора по математике: Обратитте внимание на общую закономерность 4-го и 5-го свойства: хорды в произведениях не участвуют, а сами равенства (с частями и продолжениями хорд) при сохранении обозначений являются точной копией друг друга. Также можно подметить общую структуру равенств с дугами. Репетитору по математике стоит обратить на этих особенностях внимание ученика.

6) Свойства квадрата отрезка касательной

Теорема 1: Квадрат отрезка касательной равен произведению отрезков секущей, то есть

Теорема 2:угол между касательной и секущей равен полуразности соответствующих им дуг, то есть

7) Угол между касательной и секущей

Теорема:угол между касательной и секущей, проведенными из одной точки окружности, равен поливине дуги, которую отсекает сукущая (половине центрального угла, соответствующего данной дуге).

.

Колпаков Александр Николаевич, репетитор по математике.

Уважаемый коллега, ваш материал на сайте является для меня хорошим методическим подспорьем. Спасибо.

Александр Николаевич, спасибо за методики, я восхищена Вашим трудолюбием и профессионализмом.

Уважаемый Александр Николаевич! Полезность вашего материала безгранична! Огромнейшее спасибо за справочные материалы, их оформление. Я еще не со всеми ознакомилась. Спасибо за помощь репетиторам по математике, школьным преподавателям и ученикам! Вы Учитель с большой буквы!

Спасибо за хороший материал, готовимся к олимпиаде по математике.

Александр Николаевич, большое спасибо за материал! У меня завтра экзамен, и ваш труд поможет сдать мне его на хорошую оценку. Так, как я поняла все по ваши справочникам, мне не объяснит ни один учитель — репетитор. Спасибо вам большое!

📺 Видео