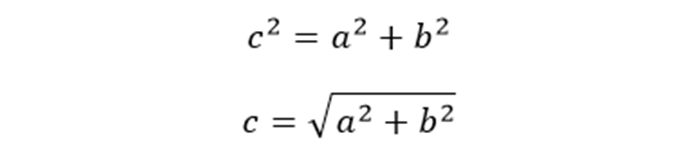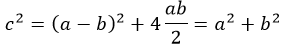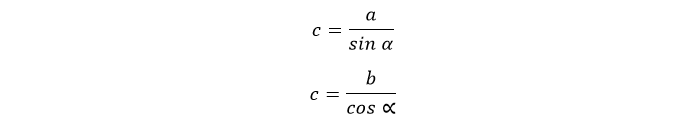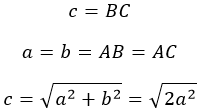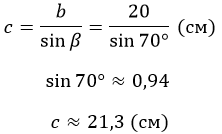Гипотеза для равнобедренного треугольника

Доказательство 1-ой гипотезы: В равнобедренном треугольнике углы при >>

Гипотеза 1:В равнобедренном треугольнике углы при основании равны. Гипотеза 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Слайд 6 из презентации «Равнобедренный треугольник и его свойства»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Равнобедренный треугольник и его свойства.ppt» можно в zip-архиве размером 809 КБ.

Треугольник

«Средняя линия треугольника» — KL – средняя линия треугольника DFE, DF =10см, FE= 12 см. Средняя линия треугольника. Является ли отрезок CD средней линией треугольника MNK? Определите стороны треугольника АВС. Чему равны отрезки DK, KF, FL, LE? Является ли отрезок EF средней линией треугольника АВС? DE — средняя линия треугольника АВС. а) Определите сторону АВ, если DE = 4 см. б) DС = 3 см, DЕ = 5 см, СЕ = 6 см.

«Теоремы Чевы и Менелая» — Теорема Чевы. Биография ученого. Проведем прямые. Менелай Александрийский. Решение. Точка. Середина стороны. Теоремы Чевы и Менелая. Прямая, параллельная биссектрисе. Точки. Равенство. Теорема Менелая. Отрезки. Точка К. ВМ-медиана. Утверждение обратное теореме.

«Треугольники» — Стороны равны. Медианы. Теорема. Треугольник. Доказательства равенства треугольников. Разносторонний. Сторона и два прилежащих к ней угла. Биссектриса. Первый признак равенства треугольников. Равносторонний. Признак равенства треугольников. Любой треугольник имеет три высоты. Доказательство. Равнобедренный.

«Равносторонний треугольник» — Внутри равностороннего треугольника. Равносторонний треугольник. Вершины. Перпендикуляры. Немецкий механик. Посетили библиотеку. Треугольники. Удивительные соотношения. Провести исследование. Равносторонние треугольники. Треугольник. Правильные треугольники.

«Свойство биссектрисы угла треугольника» — Свойство биссектрисы треугольника. Проведена биссектриса C L. Свойство биссектрисы угла треугольника. Делит противолежащую сторону на отрезки, Пропорциональные прилежащим сторонам. Биссектриса угла треугольника.

«Решение треугольников» — Определение. Сумма углов треугольника. Три задачи на решение треугольника. Решаем задачу. Значения углов. Психологическая заминка. Решение. Найди ошибку. Договоримся. Тест на определение истинности (ложности) утверждения. Решение треугольника по трём сторонам. Теорема косинусов. Психологическая разминка.

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Гипотенуза — формула, правила и примеры вычислений

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

Теорема Пифагора

Сумма квадратов катетов составляет квадрат гипотенузы:

Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.

Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.

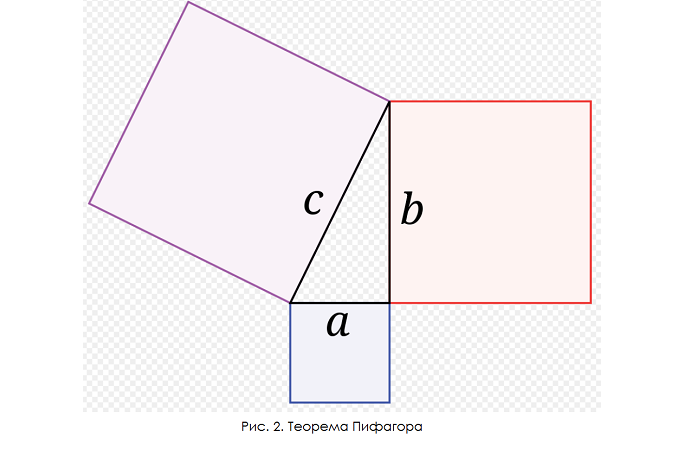
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).

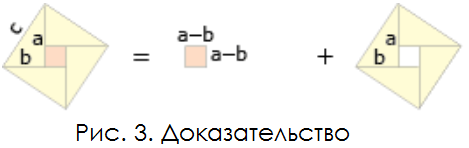
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:

В тригонометрии

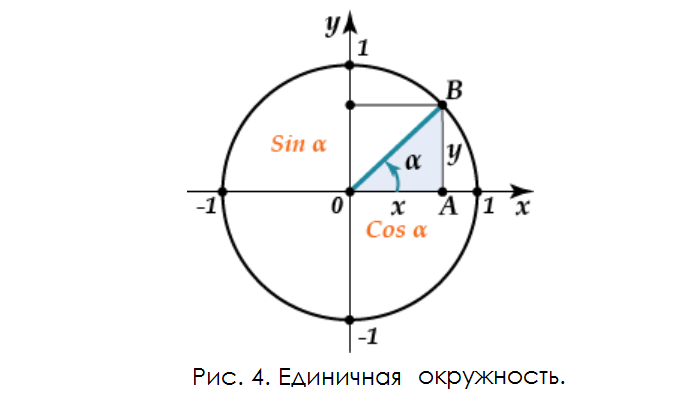
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.

В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:

sin 2 α + cos 2 α = 1

Гипотенуза прямоугольного треугольника

Связана со сторонами следующими соотношениями (см. рис. 1):

a – противолежащий α катет;

Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.

Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.

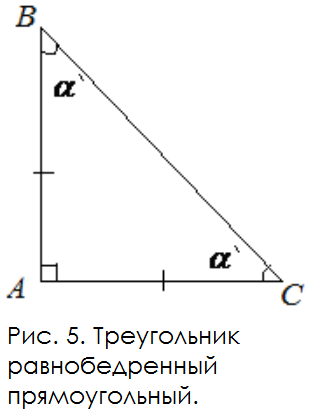
Гипотенуза равнобедренного треугольника

В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.

Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.

Пример решения задачи

Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.

AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:

Ответ: АВ = 21,3 см.

В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.

Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.

🎬 Видео